Optimal Transport Graph Neural Networks

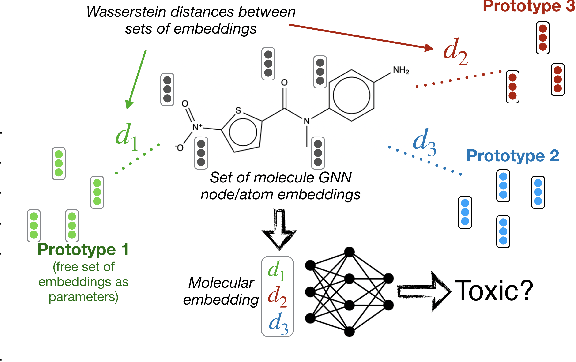
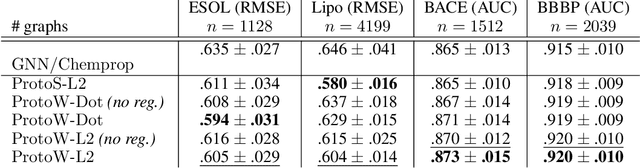
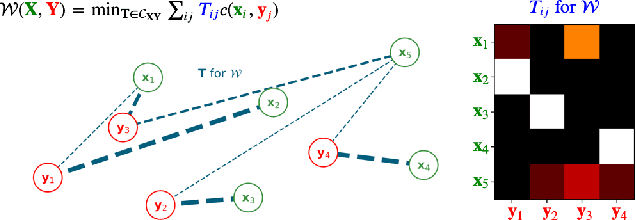
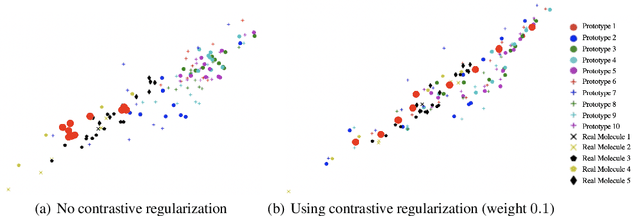
Current graph neural network (GNN) architectures naively average or sum node embeddings into an aggregated graph representation---potentially losing structural or semantic information. We here introduce OT-GNN that compute graph embeddings from optimal transport distances between the set of GNN node embeddings and "prototype" point clouds as free parameters. This allows different prototypes to highlight key facets of different graph subparts. We show that our function class on point clouds satisfies a universal approximation theorem, a fundamental property which was lost by sum aggregation. Nevertheless, empirically the model has a natural tendency to collapse back to the standard aggregation during training. We address this optimization issue by proposing an efficient noise contrastive regularizer, steering the model towards truly exploiting the optimal transport geometry. Our model consistently exhibits better generalization performance on several molecular property prediction tasks, yielding also smoother representations.