CoNOAir: A Neural Operator for Forecasting Carbon Monoxide Evolution in Cities

Carbon Monoxide (CO) is a dominant pollutant in urban areas due to the energy generation from fossil fuels for industry, automobile, and domestic requirements. Forecasting the evolution of CO in real-time can enable the deployment of effective early warning systems and intervention strategies. However, the computational cost associated with the physics and chemistry-based simulation makes it prohibitive to implement such a model at the city and country scale. To address this challenge, here, we present a machine learning model based on neural operator, namely, Complex Neural Operator for Air Quality (CoNOAir), that can effectively forecast CO concentrations. We demonstrate this by developing a country-level model for short-term (hourly) and long-term (72-hour) forecasts of CO concentrations. Our model outperforms state-of-the-art models such as Fourier neural operators (FNO) and provides reliable predictions for both short and long-term forecasts. We further analyse the capability of the model to capture extreme events and generate forecasts in urban cities in India. Interestingly, we observe that the model predicts the next hour CO concentrations with R2 values greater than 0.95 for all the cities considered. The deployment of such a model can greatly assist the governing bodies to provide early warning, plan intervention strategies, and develop effective strategies by considering several what-if scenarios. Altogether, the present approach could provide a fillip to real-time predictions of CO pollution in urban cities.

Industrial-scale Prediction of Cement Clinker Phases using Machine Learning

Cement production, exceeding 4.1 billion tonnes and contributing 2.4 tonnes of CO2 annually, faces critical challenges in quality control and process optimization. While traditional process models for cement manufacturing are confined to steady-state conditions with limited predictive capability for mineralogical phases, modern plants operate under dynamic conditions that demand real-time quality assessment. Here, exploiting a comprehensive two-year operational dataset from an industrial cement plant, we present a machine learning framework that accurately predicts clinker mineralogy from process data. Our model achieves unprecedented prediction accuracy for major clinker phases while requiring minimal input parameters, demonstrating robust performance under varying operating conditions. Through post-hoc explainable algorithms, we interpret the hierarchical relationships between clinker oxides and phase formation, providing insights into the functioning of an otherwise black-box model. This digital twin framework can potentially enable real-time optimization of cement production, thereby providing a route toward reducing material waste and ensuring quality while reducing the associated emissions under real plant conditions. Our approach represents a significant advancement in industrial process control, offering a scalable solution for sustainable cement manufacturing.

Foundational Large Language Models for Materials Research

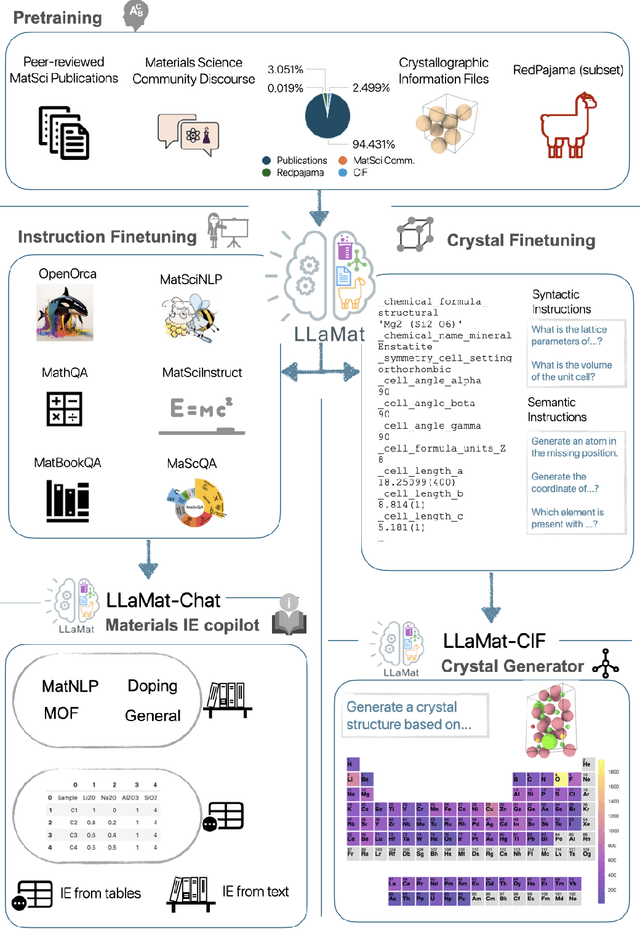
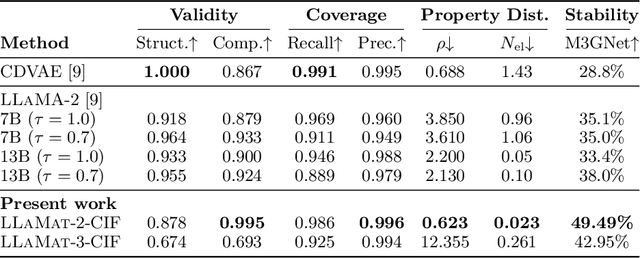
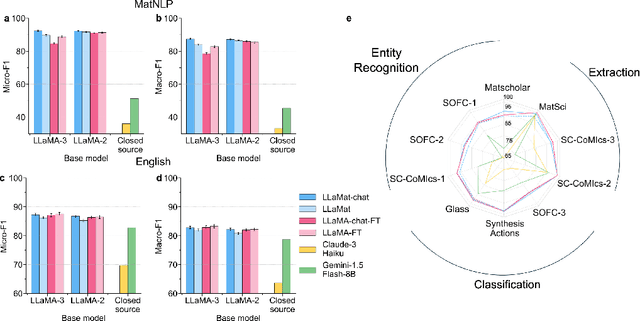
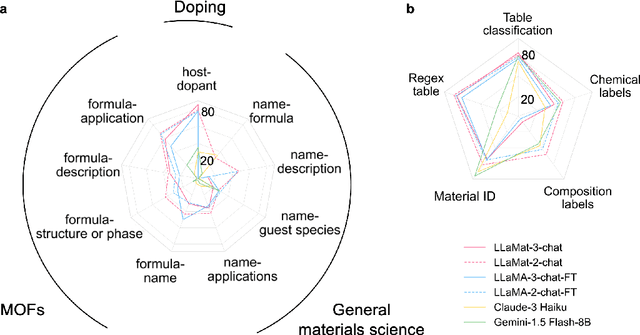
Materials discovery and development are critical for addressing global challenges. Yet, the exponential growth in materials science literature comprising vast amounts of textual data has created significant bottlenecks in knowledge extraction, synthesis, and scientific reasoning. Large Language Models (LLMs) offer unprecedented opportunities to accelerate materials research through automated analysis and prediction. Still, their effective deployment requires domain-specific adaptation for understanding and solving domain-relevant tasks. Here, we present LLaMat, a family of foundational models for materials science developed through continued pretraining of LLaMA models on an extensive corpus of materials literature and crystallographic data. Through systematic evaluation, we demonstrate that LLaMat excels in materials-specific NLP and structured information extraction while maintaining general linguistic capabilities. The specialized LLaMat-CIF variant demonstrates unprecedented capabilities in crystal structure generation, predicting stable crystals with high coverage across the periodic table. Intriguingly, despite LLaMA-3's superior performance in comparison to LLaMA-2, we observe that LLaMat-2 demonstrates unexpectedly enhanced domain-specific performance across diverse materials science tasks, including structured information extraction from text and tables, more particularly in crystal structure generation, a potential adaptation rigidity in overtrained LLMs. Altogether, the present work demonstrates the effectiveness of domain adaptation towards developing practically deployable LLM copilots for materials research. Beyond materials science, our findings reveal important considerations for domain adaptation of LLMs, such as model selection, training methodology, and domain-specific performance, which may influence the development of specialized scientific AI systems.

Probing the limitations of multimodal language models for chemistry and materials research

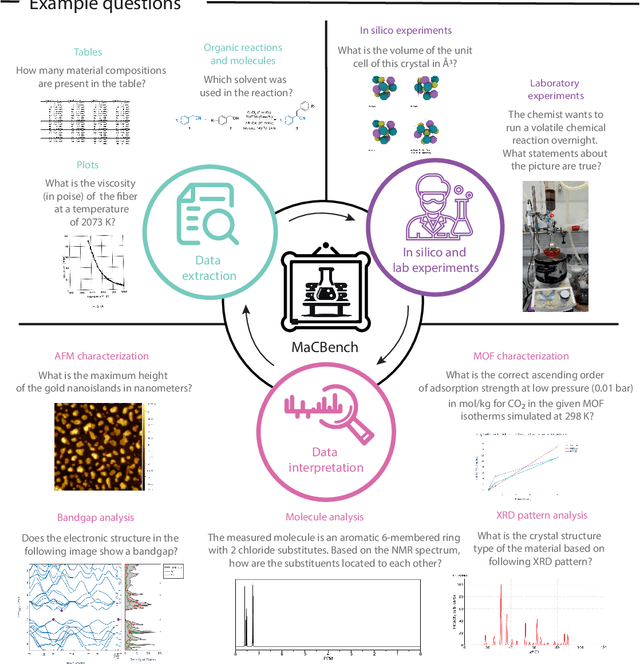
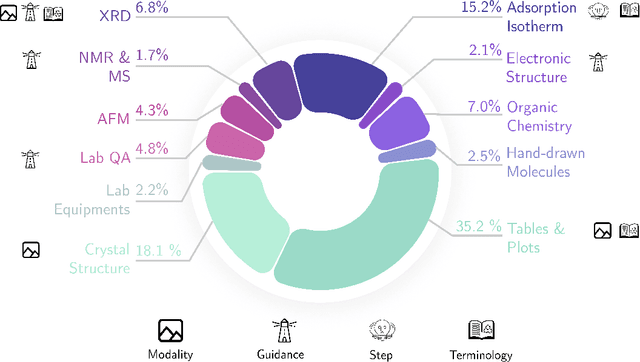
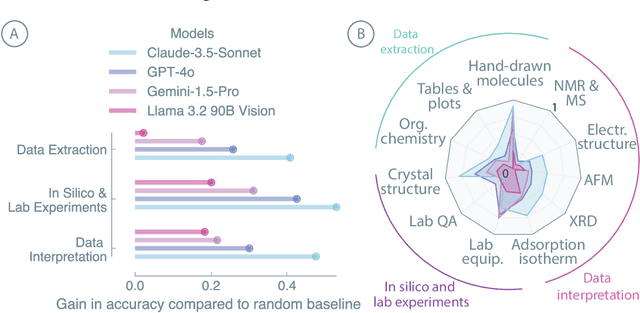
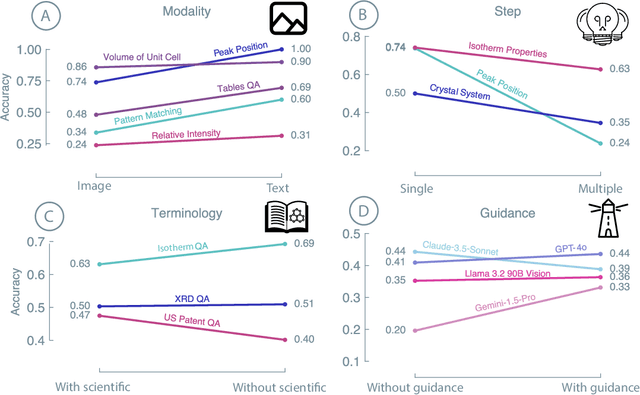
Recent advancements in artificial intelligence have sparked interest in scientific assistants that could support researchers across the full spectrum of scientific workflows, from literature review to experimental design and data analysis. A key capability for such systems is the ability to process and reason about scientific information in both visual and textual forms - from interpreting spectroscopic data to understanding laboratory setups. Here, we introduce MaCBench, a comprehensive benchmark for evaluating how vision-language models handle real-world chemistry and materials science tasks across three core aspects: data extraction, experimental understanding, and results interpretation. Through a systematic evaluation of leading models, we find that while these systems show promising capabilities in basic perception tasks - achieving near-perfect performance in equipment identification and standardized data extraction - they exhibit fundamental limitations in spatial reasoning, cross-modal information synthesis, and multi-step logical inference. Our insights have important implications beyond chemistry and materials science, suggesting that developing reliable multimodal AI scientific assistants may require advances in curating suitable training data and approaches to training those models.

TAGMol: Target-Aware Gradient-guided Molecule Generation

3D generative models have shown significant promise in structure-based drug design (SBDD), particularly in discovering ligands tailored to specific target binding sites. Existing algorithms often focus primarily on ligand-target binding, characterized by binding affinity. Moreover, models trained solely on target-ligand distribution may fall short in addressing the broader objectives of drug discovery, such as the development of novel ligands with desired properties like drug-likeness, and synthesizability, underscoring the multifaceted nature of the drug design process. To overcome these challenges, we decouple the problem into molecular generation and property prediction. The latter synergistically guides the diffusion sampling process, facilitating guided diffusion and resulting in the creation of meaningful molecules with the desired properties. We call this guided molecular generation process as TAGMol. Through experiments on benchmark datasets, TAGMol demonstrates superior performance compared to state-of-the-art baselines, achieving a 22% improvement in average Vina Score and yielding favorable outcomes in essential auxiliary properties. This establishes TAGMol as a comprehensive framework for drug generation.

MaScQA: A Question Answering Dataset for Investigating Materials Science Knowledge of Large Language Models

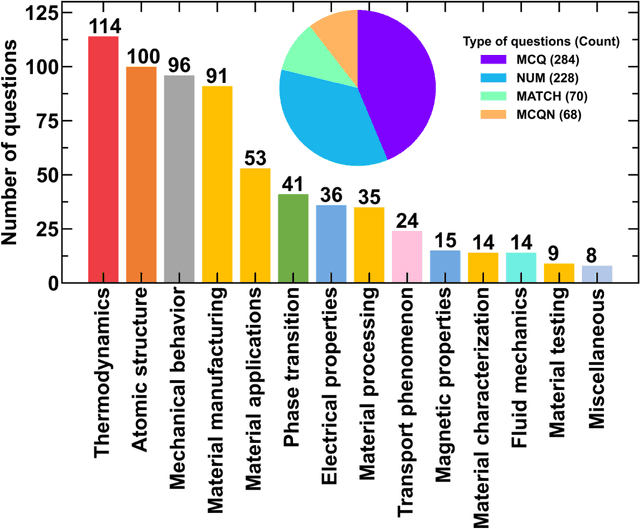
Information extraction and textual comprehension from materials literature are vital for developing an exhaustive knowledge base that enables accelerated materials discovery. Language models have demonstrated their capability to answer domain-specific questions and retrieve information from knowledge bases. However, there are no benchmark datasets in the materials domain that can evaluate the understanding of the key concepts by these language models. In this work, we curate a dataset of 650 challenging questions from the materials domain that require the knowledge and skills of a materials student who has cleared their undergraduate degree. We classify these questions based on their structure and the materials science domain-based subcategories. Further, we evaluate the performance of GPT-3.5 and GPT-4 models on solving these questions via zero-shot and chain of thought prompting. It is observed that GPT-4 gives the best performance (~62% accuracy) as compared to GPT-3.5. Interestingly, in contrast to the general observation, no significant improvement in accuracy is observed with the chain of thought prompting. To evaluate the limitations, we performed an error analysis, which revealed conceptual errors (~64%) as the major contributor compared to computational errors (~36%) towards the reduced performance of LLMs. We hope that the dataset and analysis performed in this work will promote further research in developing better materials science domain-specific LLMs and strategies for information extraction.

Graph Neural Stochastic Differential Equations for Learning Brownian Dynamics

Neural networks (NNs) that exploit strong inductive biases based on physical laws and symmetries have shown remarkable success in learning the dynamics of physical systems directly from their trajectory. However, these works focus only on the systems that follow deterministic dynamics, for instance, Newtonian or Hamiltonian dynamics. Here, we propose a framework, namely Brownian graph neural networks (BROGNET), combining stochastic differential equations (SDEs) and GNNs to learn Brownian dynamics directly from the trajectory. We theoretically show that BROGNET conserves the linear momentum of the system, which in turn, provides superior performance on learning dynamics as revealed empirically. We demonstrate this approach on several systems, namely, linear spring, linear spring with binary particle types, and non-linear spring systems, all following Brownian dynamics at finite temperatures. We show that BROGNET significantly outperforms proposed baselines across all the benchmarked Brownian systems. In addition, we demonstrate zero-shot generalizability of BROGNET to simulate unseen system sizes that are two orders of magnitude larger and to different temperatures than those used during training. Altogether, our study contributes to advancing the understanding of the intricate dynamics of Brownian motion and demonstrates the effectiveness of graph neural networks in modeling such complex systems.

StriderNET: A Graph Reinforcement Learning Approach to Optimize Atomic Structures on Rough Energy Landscapes

Optimization of atomic structures presents a challenging problem, due to their highly rough and non-convex energy landscape, with wide applications in the fields of drug design, materials discovery, and mechanics. Here, we present a graph reinforcement learning approach, StriderNET, that learns a policy to displace the atoms towards low energy configurations. We evaluate the performance of StriderNET on three complex atomic systems, namely, binary Lennard-Jones particles, calcium silicate hydrates gel, and disordered silicon. We show that StriderNET outperforms all classical optimization algorithms and enables the discovery of a lower energy minimum. In addition, StriderNET exhibits a higher rate of reaching minima with energies, as confirmed by the average over multiple realizations. Finally, we show that StriderNET exhibits inductivity to unseen system sizes that are an order of magnitude different from the training system.

Cementron: Machine Learning the Constituent Phases in Cement Clinker from Optical Images

Cement is the most used construction material. The performance of cement hydrate depends on the constituent phases, viz. alite, belite, aluminate, and ferrites present in the cement clinker, both qualitatively and quantitatively. Traditionally, clinker phases are analyzed from optical images relying on a domain expert and simple image processing techniques. However, the non-uniformity of the images, variations in the geometry and size of the phases, and variabilities in the experimental approaches and imaging methods make it challenging to obtain the phases. Here, we present a machine learning (ML) approach to detect clinker microstructure phases automatically. To this extent, we create the first annotated dataset of cement clinker by segmenting alite and belite particles. Further, we use supervised ML methods to train models for identifying alite and belite regions. Specifically, we finetune the image detection and segmentation model Detectron-2 on the cement microstructure to develop a model for detecting the cement phases, namely, Cementron. We demonstrate that Cementron, trained only on literature data, works remarkably well on new images obtained from our experiments, demonstrating its generalizability. We make Cementron available for public use.

Predicting Oxide Glass Properties with Low Complexity Neural Network and Physical and Chemical Descriptors

Due to their disordered structure, glasses present a unique challenge in predicting the composition-property relationships. Recently, several attempts have been made to predict the glass properties using machine learning techniques. However, these techniques have the limitations, namely, (i) predictions are limited to the components that are present in the original dataset, and (ii) predictions towards the extreme values of the properties, important regions for new materials discovery, are not very reliable due to the sparse datapoints in this region. To address these challenges, here we present a low complexity neural network (LCNN) that provides improved performance in predicting the properties of oxide glasses. In addition, we combine the LCNN with physical and chemical descriptors that allow the development of universal models that can provide predictions for components beyond the training set. By training on a large dataset (~50000) of glass components, we show the LCNN outperforms state-of-the-art algorithms such as XGBoost. In addition, we interpret the LCNN models using Shapely additive explanations to gain insights into the role played by the descriptors in governing the property. Finally, we demonstrate the universality of the LCNN models by predicting the properties for glasses with new components that were not present in the original training set. Altogether, the present approach provides a promising direction towards accelerated discovery of novel glass compositions.