Bonsai: Gradient-free Graph Distillation for Node Classification

Graph distillation has emerged as a promising avenue to enable scalable training of GNNs by compressing the training dataset while preserving essential graph characteristics. Our study uncovers significant shortcomings in current graph distillation techniques. First, the majority of the algorithms paradoxically require training on the full dataset to perform distillation. Second, due to their gradient-emulating approach, these methods require fresh distillation for any change in hyperparameters or GNN architecture, limiting their flexibility and reusability. Finally, they fail to achieve substantial size reduction due to synthesizing fully-connected, edge-weighted graphs. To address these challenges, we present Bonsai, a novel graph distillation method empowered by the observation that \textit{computation trees} form the fundamental processing units of message-passing GNNs. Bonsai distills datasets by encoding a careful selection of \textit{exemplar} trees that maximize the representation of all computation trees in the training set. This unique approach imparts Bonsai as the first linear-time, model-agnostic graph distillation algorithm for node classification that outperforms existing baselines across $6$ real-world datasets on accuracy, while being $22$ times faster on average. Bonsai is grounded in rigorous mathematical guarantees on the adopted approximation strategies making it robust to GNN architectures, datasets, and parameters.

TAGMol: Target-Aware Gradient-guided Molecule Generation

3D generative models have shown significant promise in structure-based drug design (SBDD), particularly in discovering ligands tailored to specific target binding sites. Existing algorithms often focus primarily on ligand-target binding, characterized by binding affinity. Moreover, models trained solely on target-ligand distribution may fall short in addressing the broader objectives of drug discovery, such as the development of novel ligands with desired properties like drug-likeness, and synthesizability, underscoring the multifaceted nature of the drug design process. To overcome these challenges, we decouple the problem into molecular generation and property prediction. The latter synergistically guides the diffusion sampling process, facilitating guided diffusion and resulting in the creation of meaningful molecules with the desired properties. We call this guided molecular generation process as TAGMol. Through experiments on benchmark datasets, TAGMol demonstrates superior performance compared to state-of-the-art baselines, achieving a 22% improvement in average Vina Score and yielding favorable outcomes in essential auxiliary properties. This establishes TAGMol as a comprehensive framework for drug generation.

GRAPHGINI: Fostering Individual and Group Fairness in Graph Neural Networks

We address the growing apprehension that GNNs, in the absence of fairness constraints, might produce biased decisions that disproportionately affect underprivileged groups or individuals. Departing from previous work, we introduce for the first time a method for incorporating the Gini coefficient as a measure of fairness to be used within the GNN framework. Our proposal, GRAPHGINI, works with the two different goals of individual and group fairness in a single system, while maintaining high prediction accuracy. GRAPHGINI enforces individual fairness through learnable attention scores that help in aggregating more information through similar nodes. A heuristic-based maximum Nash social welfare constraint ensures the maximum possible group fairness. Both the individual fairness constraint and the group fairness constraint are stated in terms of a differentiable approximation of the Gini coefficient. This approximation is a contribution that is likely to be of interest even beyond the scope of the problem studied in this paper. Unlike other state-of-the-art, GRAPHGINI automatically balances all three optimization objectives (utility, individual, and group fairness) of the GNN and is free from any manual tuning of weight parameters. Extensive experimentation on real-world datasets showcases the efficacy of GRAPHGINI in making significant improvements in individual fairness compared to all currently available state-of-the-art methods while maintaining utility and group equality.

EUGENE: Explainable Unsupervised Approximation of Graph Edit Distance

The need to identify graphs having small structural distance from a query arises in biology, chemistry, recommender systems, and social network analysis. Among several methods to measure inter graph distance, Graph Edit Distance (GED) is preferred for its comprehensibility, yet hindered by the NP-hardness of its computation. State-of-the-art GED approximations predominantly employ neural methods, which, however, (i) lack an explanatory edit path corresponding to the approximated GED; (ii) require the NP-hard generation of ground-truth GEDs for training; and (iii) necessitate separate training on each dataset. In this paper, we propose an efficient algebraic unsuper vised method, EUGENE, that approximates GED and yields edit paths corresponding to the approx imated cost, while eliminating the need for ground truth generation and data-specific training. Extensive experimental evaluation demonstrates that the aforementioned benefits of EUGENE do not come at the cost of efficacy. Specifically, EUGENE consistently ranks among the most accurate methods across all of the benchmark datasets and outperforms majority of the neural approaches.

NeuroCUT: A Neural Approach for Robust Graph Partitioning

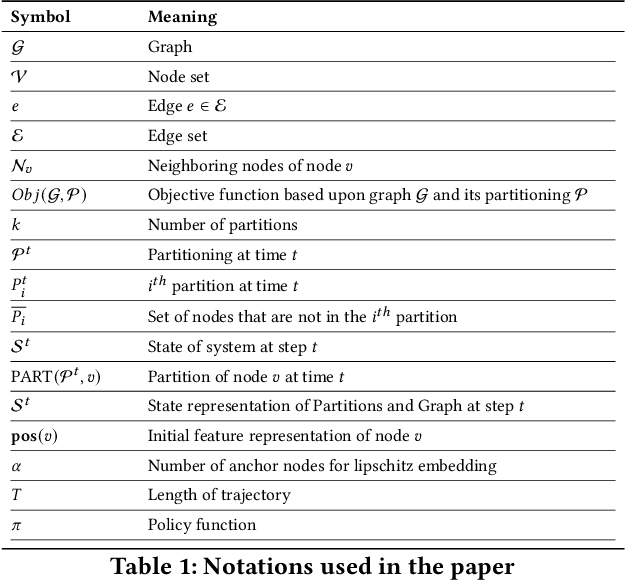
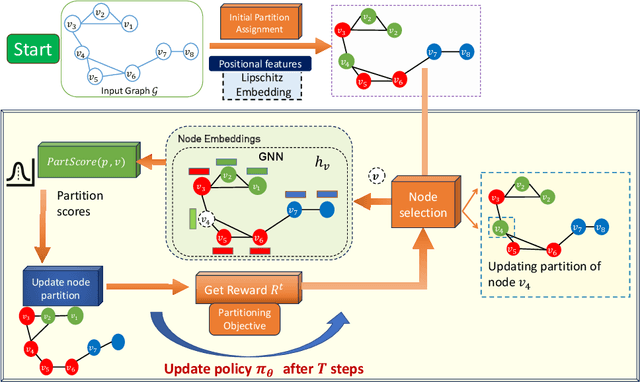
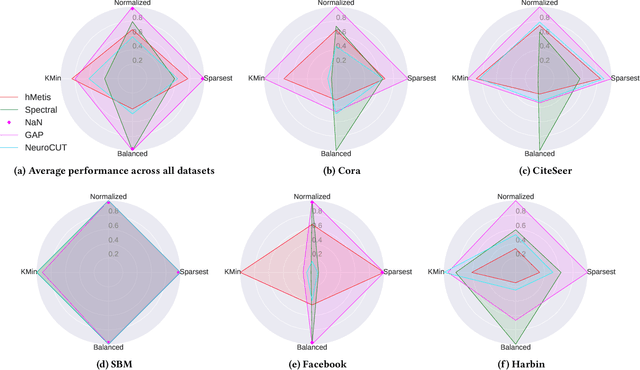
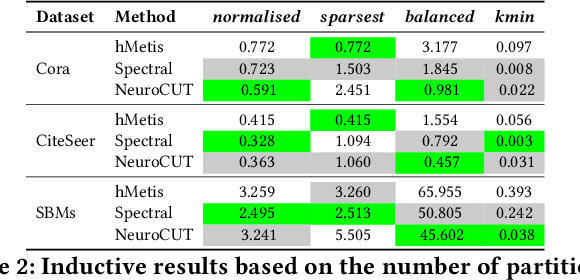
Graph partitioning aims to divide a graph into $k$ disjoint subsets while optimizing a specific partitioning objective. The majority of formulations related to graph partitioning exhibit NP-hardness due to their combinatorial nature. As a result, conventional approximation algorithms rely on heuristic methods, sometimes with approximation guarantees and sometimes without. Unfortunately, traditional approaches are tailored for specific partitioning objectives and do not generalize well across other known partitioning objectives from the literature. To overcome this limitation, and learn heuristics from the data directly, neural approaches have emerged, demonstrating promising outcomes. In this study, we extend this line of work through a novel framework, NeuroCut. NeuroCut introduces two key innovations over prevailing methodologies. First, it is inductive to both graph topology and the partition count, which is provided at query time. Second, by leveraging a reinforcement learning based framework over node representations derived from a graph neural network, NeuroCut can accommodate any optimization objective, even those encompassing non-differentiable functions. Through empirical evaluation, we demonstrate that NeuroCut excels in identifying high-quality partitions, showcases strong generalization across a wide spectrum of partitioning objectives, and exhibits resilience to topological modifications.

Mirage: Model-Agnostic Graph Distillation for Graph Classification

GNNs, like other deep learning models, are data and computation hungry. There is a pressing need to scale training of GNNs on large datasets to enable their usage on low-resource environments. Graph distillation is an effort in that direction with the aim to construct a smaller synthetic training set from the original training data without significantly compromising model performance. While initial efforts are promising, this work is motivated by two key observations: (1) Existing graph distillation algorithms themselves rely on training with the full dataset, which undermines the very premise of graph distillation. (2) The distillation process is specific to the target GNN architecture and hyper-parameters and thus not robust to changes in the modeling pipeline. We circumvent these limitations by designing a distillation algorithm called Mirage for graph classification. Mirage is built on the insight that a message-passing GNN decomposes the input graph into a multiset of computation trees. Furthermore, the frequency distribution of computation trees is often skewed in nature, enabling us to condense this data into a concise distilled summary. By compressing the computation data itself, as opposed to emulating gradient flows on the original training set-a prevalent approach to date-Mirage transforms into an unsupervised and architecture-agnostic distillation algorithm. Extensive benchmarking on real-world datasets underscores Mirage's superiority, showcasing enhanced generalization accuracy, data compression, and distillation efficiency when compared to state-of-the-art baselines.

EGraFFBench: Evaluation of Equivariant Graph Neural Network Force Fields for Atomistic Simulations

Equivariant graph neural networks force fields (EGraFFs) have shown great promise in modelling complex interactions in atomic systems by exploiting the graphs' inherent symmetries. Recent works have led to a surge in the development of novel architectures that incorporate equivariance-based inductive biases alongside architectural innovations like graph transformers and message passing to model atomic interactions. However, thorough evaluations of these deploying EGraFFs for the downstream task of real-world atomistic simulations, is lacking. To this end, here we perform a systematic benchmarking of 6 EGraFF algorithms (NequIP, Allegro, BOTNet, MACE, Equiformer, TorchMDNet), with the aim of understanding their capabilities and limitations for realistic atomistic simulations. In addition to our thorough evaluation and analysis on eight existing datasets based on the benchmarking literature, we release two new benchmark datasets, propose four new metrics, and three new challenging tasks. The new datasets and tasks evaluate the performance of EGraFF to out-of-distribution data, in terms of different crystal structures, temperatures, and new molecules. Interestingly, evaluation of the EGraFF models based on dynamic simulations reveals that having a lower error on energy or force does not guarantee stable or reliable simulation or faithful replication of the atomic structures. Moreover, we find that no model clearly outperforms other models on all datasets and tasks. Importantly, we show that the performance of all the models on out-of-distribution datasets is unreliable, pointing to the need for the development of a foundation model for force fields that can be used in real-world simulations. In summary, this work establishes a rigorous framework for evaluating machine learning force fields in the context of atomic simulations and points to open research challenges within this domain.

GNNX-BENCH: Unravelling the Utility of Perturbation-based GNN Explainers through In-depth Benchmarking

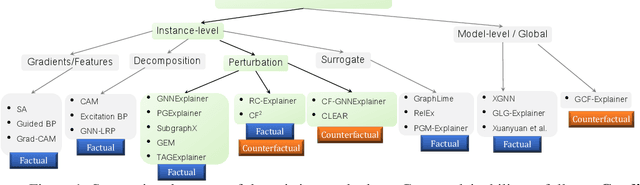
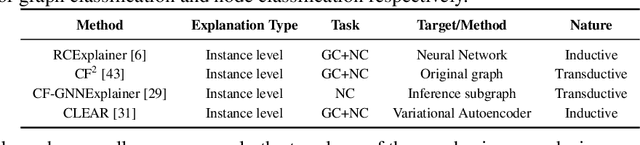
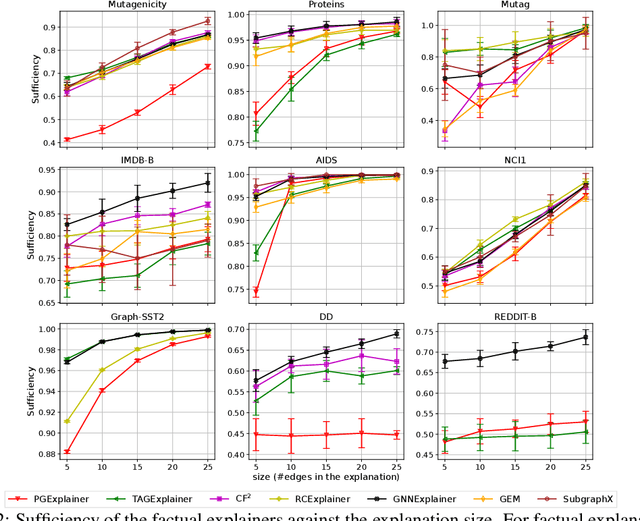
Numerous explainability methods have been proposed to shed light on the inner workings of GNNs. Despite the inclusion of empirical evaluations in all the proposed algorithms, the interrogative aspects of these evaluations lack diversity. As a result, various facets of explainability pertaining to GNNs, such as a comparative analysis of counterfactual reasoners, their stability to variational factors such as different GNN architectures, noise, stochasticity in non-convex loss surfaces, feasibility amidst domain constraints, and so forth, have yet to be formally investigated. Motivated by this need, we present a benchmarking study on perturbation-based explainability methods for GNNs, aiming to systematically evaluate and compare a wide range of explainability techniques. Among the key findings of our study, we identify the Pareto-optimal methods that exhibit superior efficacy and stability in the presence of noise. Nonetheless, our study reveals that all algorithms are affected by stability issues when faced with noisy data. Furthermore, we have established that the current generation of counterfactual explainers often fails to provide feasible recourses due to violations of topological constraints encoded by domain-specific considerations. Overall, this benchmarking study empowers stakeholders in the field of GNNs with a comprehensive understanding of the state-of-the-art explainability methods, potential research problems for further enhancement, and the implications of their application in real-world scenarios.

Discovering Symbolic Laws Directly from Trajectories with Hamiltonian Graph Neural Networks

The time evolution of physical systems is described by differential equations, which depend on abstract quantities like energy and force. Traditionally, these quantities are derived as functionals based on observables such as positions and velocities. Discovering these governing symbolic laws is the key to comprehending the interactions in nature. Here, we present a Hamiltonian graph neural network (HGNN), a physics-enforced GNN that learns the dynamics of systems directly from their trajectory. We demonstrate the performance of HGNN on n-springs, n-pendulums, gravitational systems, and binary Lennard Jones systems; HGNN learns the dynamics in excellent agreement with the ground truth from small amounts of data. We also evaluate the ability of HGNN to generalize to larger system sizes, and to hybrid spring-pendulum system that is a combination of two original systems (spring and pendulum) on which the models are trained independently. Finally, employing symbolic regression on the learned HGNN, we infer the underlying equations relating the energy functionals, even for complex systems such as the binary Lennard-Jones liquid. Our framework facilitates the interpretable discovery of interaction laws directly from physical system trajectories. Furthermore, this approach can be extended to other systems with topology-dependent dynamics, such as cells, polydisperse gels, or deformable bodies.

Graph Neural Stochastic Differential Equations for Learning Brownian Dynamics

Neural networks (NNs) that exploit strong inductive biases based on physical laws and symmetries have shown remarkable success in learning the dynamics of physical systems directly from their trajectory. However, these works focus only on the systems that follow deterministic dynamics, for instance, Newtonian or Hamiltonian dynamics. Here, we propose a framework, namely Brownian graph neural networks (BROGNET), combining stochastic differential equations (SDEs) and GNNs to learn Brownian dynamics directly from the trajectory. We theoretically show that BROGNET conserves the linear momentum of the system, which in turn, provides superior performance on learning dynamics as revealed empirically. We demonstrate this approach on several systems, namely, linear spring, linear spring with binary particle types, and non-linear spring systems, all following Brownian dynamics at finite temperatures. We show that BROGNET significantly outperforms proposed baselines across all the benchmarked Brownian systems. In addition, we demonstrate zero-shot generalizability of BROGNET to simulate unseen system sizes that are two orders of magnitude larger and to different temperatures than those used during training. Altogether, our study contributes to advancing the understanding of the intricate dynamics of Brownian motion and demonstrates the effectiveness of graph neural networks in modeling such complex systems.