GNNX-BENCH: Unravelling the Utility of Perturbation-based GNN Explainers through In-depth Benchmarking

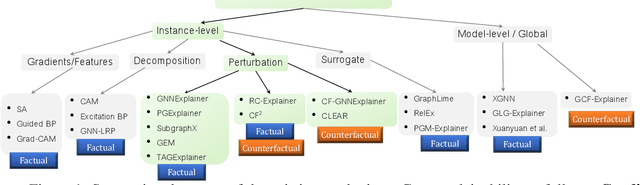
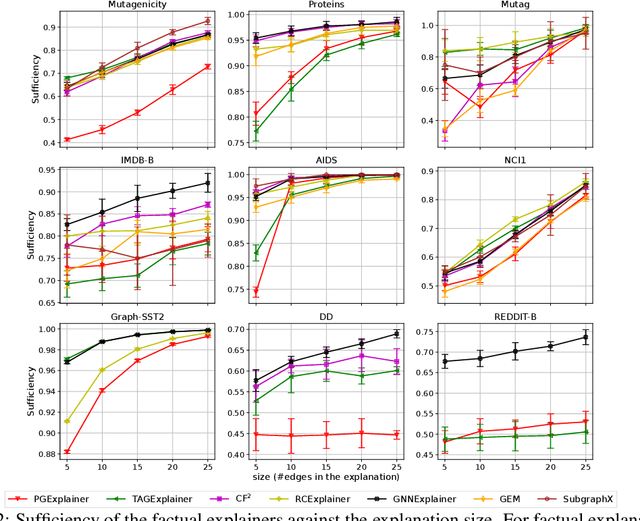
Numerous explainability methods have been proposed to shed light on the inner workings of GNNs. Despite the inclusion of empirical evaluations in all the proposed algorithms, the interrogative aspects of these evaluations lack diversity. As a result, various facets of explainability pertaining to GNNs, such as a comparative analysis of counterfactual reasoners, their stability to variational factors such as different GNN architectures, noise, stochasticity in non-convex loss surfaces, feasibility amidst domain constraints, and so forth, have yet to be formally investigated. Motivated by this need, we present a benchmarking study on perturbation-based explainability methods for GNNs, aiming to systematically evaluate and compare a wide range of explainability techniques. Among the key findings of our study, we identify the Pareto-optimal methods that exhibit superior efficacy and stability in the presence of noise. Nonetheless, our study reveals that all algorithms are affected by stability issues when faced with noisy data. Furthermore, we have established that the current generation of counterfactual explainers often fails to provide feasible recourses due to violations of topological constraints encoded by domain-specific considerations. Overall, this benchmarking study empowers stakeholders in the field of GNNs with a comprehensive understanding of the state-of-the-art explainability methods, potential research problems for further enhancement, and the implications of their application in real-world scenarios.

Empowering Counterfactual Reasoning over Graph Neural Networks through Inductivity

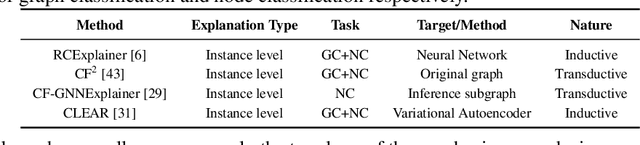
Graph neural networks (GNNs) have various practical applications, such as drug discovery, recommendation engines, and chip design. However, GNNs lack transparency as they cannot provide understandable explanations for their predictions. To address this issue, counterfactual reasoning is used. The main goal is to make minimal changes to the input graph of a GNN in order to alter its prediction. While several algorithms have been proposed for counterfactual explanations of GNNs, most of them have two main drawbacks. Firstly, they only consider edge deletions as perturbations. Secondly, the counterfactual explanation models are transductive, meaning they do not generalize to unseen data. In this study, we introduce an inductive algorithm called INDUCE, which overcomes these limitations. By conducting extensive experiments on several datasets, we demonstrate that incorporating edge additions leads to better counterfactual results compared to the existing methods. Moreover, the inductive modeling approach allows INDUCE to directly predict counterfactual perturbations without requiring instance-specific training. This results in significant computational speed improvements compared to baseline methods and enables scalable counterfactual analysis for GNNs.