Foundational Large Language Models for Materials Research

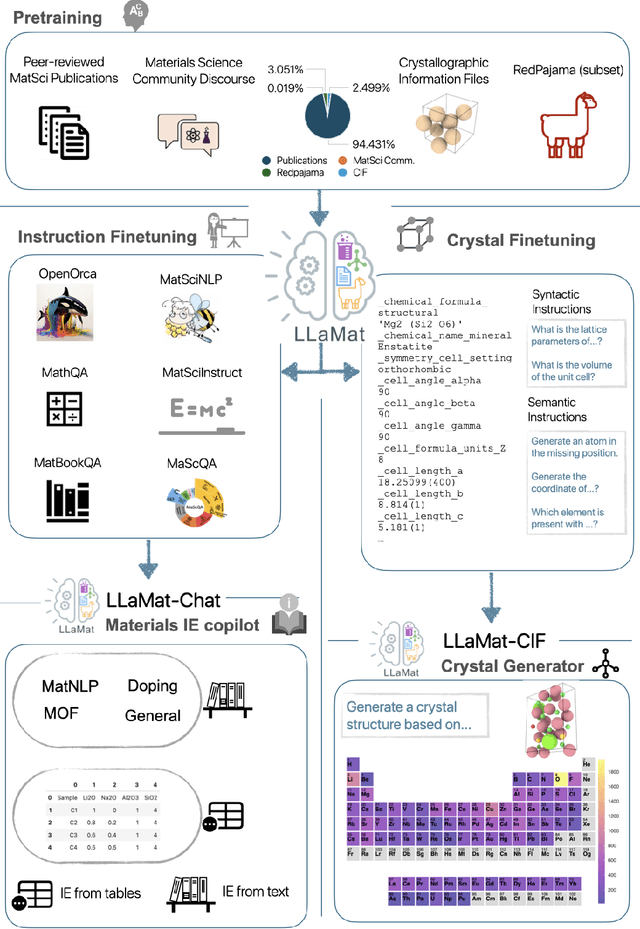
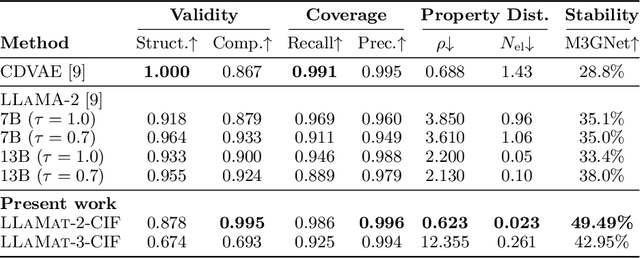
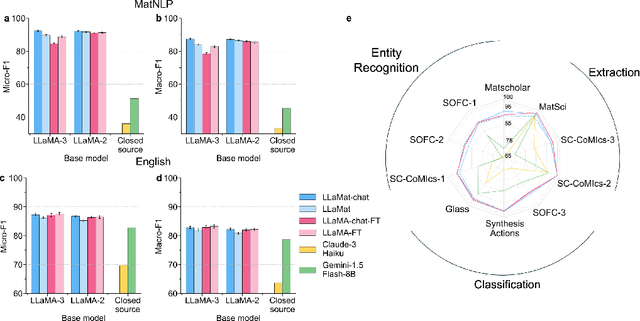
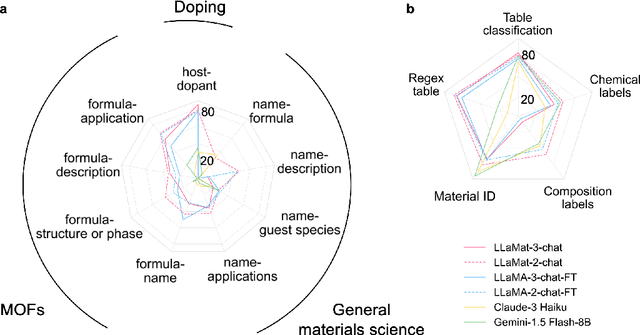
Materials discovery and development are critical for addressing global challenges. Yet, the exponential growth in materials science literature comprising vast amounts of textual data has created significant bottlenecks in knowledge extraction, synthesis, and scientific reasoning. Large Language Models (LLMs) offer unprecedented opportunities to accelerate materials research through automated analysis and prediction. Still, their effective deployment requires domain-specific adaptation for understanding and solving domain-relevant tasks. Here, we present LLaMat, a family of foundational models for materials science developed through continued pretraining of LLaMA models on an extensive corpus of materials literature and crystallographic data. Through systematic evaluation, we demonstrate that LLaMat excels in materials-specific NLP and structured information extraction while maintaining general linguistic capabilities. The specialized LLaMat-CIF variant demonstrates unprecedented capabilities in crystal structure generation, predicting stable crystals with high coverage across the periodic table. Intriguingly, despite LLaMA-3's superior performance in comparison to LLaMA-2, we observe that LLaMat-2 demonstrates unexpectedly enhanced domain-specific performance across diverse materials science tasks, including structured information extraction from text and tables, more particularly in crystal structure generation, a potential adaptation rigidity in overtrained LLMs. Altogether, the present work demonstrates the effectiveness of domain adaptation towards developing practically deployable LLM copilots for materials research. Beyond materials science, our findings reveal important considerations for domain adaptation of LLMs, such as model selection, training methodology, and domain-specific performance, which may influence the development of specialized scientific AI systems.

EGraFFBench: Evaluation of Equivariant Graph Neural Network Force Fields for Atomistic Simulations

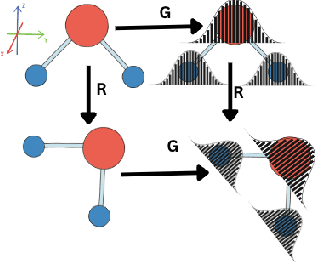
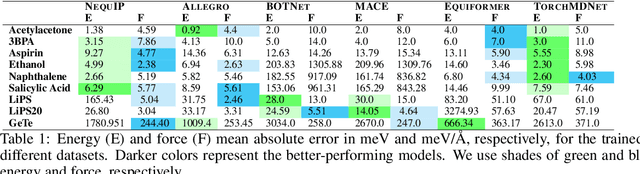
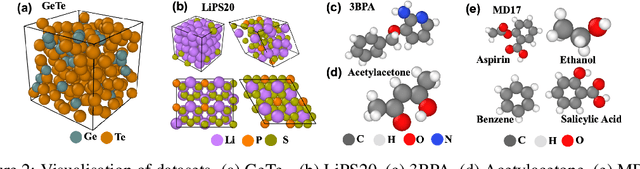
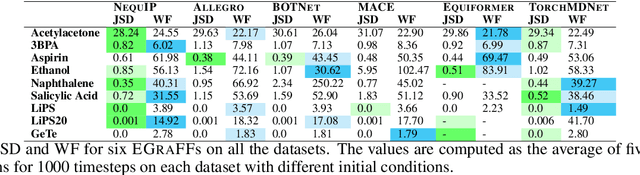
Equivariant graph neural networks force fields (EGraFFs) have shown great promise in modelling complex interactions in atomic systems by exploiting the graphs' inherent symmetries. Recent works have led to a surge in the development of novel architectures that incorporate equivariance-based inductive biases alongside architectural innovations like graph transformers and message passing to model atomic interactions. However, thorough evaluations of these deploying EGraFFs for the downstream task of real-world atomistic simulations, is lacking. To this end, here we perform a systematic benchmarking of 6 EGraFF algorithms (NequIP, Allegro, BOTNet, MACE, Equiformer, TorchMDNet), with the aim of understanding their capabilities and limitations for realistic atomistic simulations. In addition to our thorough evaluation and analysis on eight existing datasets based on the benchmarking literature, we release two new benchmark datasets, propose four new metrics, and three new challenging tasks. The new datasets and tasks evaluate the performance of EGraFF to out-of-distribution data, in terms of different crystal structures, temperatures, and new molecules. Interestingly, evaluation of the EGraFF models based on dynamic simulations reveals that having a lower error on energy or force does not guarantee stable or reliable simulation or faithful replication of the atomic structures. Moreover, we find that no model clearly outperforms other models on all datasets and tasks. Importantly, we show that the performance of all the models on out-of-distribution datasets is unreliable, pointing to the need for the development of a foundation model for force fields that can be used in real-world simulations. In summary, this work establishes a rigorous framework for evaluating machine learning force fields in the context of atomic simulations and points to open research challenges within this domain.

StriderNET: A Graph Reinforcement Learning Approach to Optimize Atomic Structures on Rough Energy Landscapes

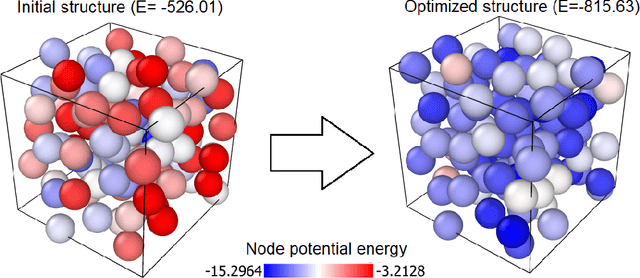
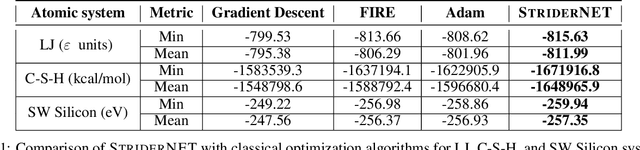
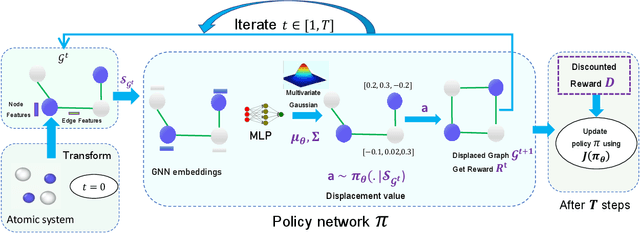
Optimization of atomic structures presents a challenging problem, due to their highly rough and non-convex energy landscape, with wide applications in the fields of drug design, materials discovery, and mechanics. Here, we present a graph reinforcement learning approach, StriderNET, that learns a policy to displace the atoms towards low energy configurations. We evaluate the performance of StriderNET on three complex atomic systems, namely, binary Lennard-Jones particles, calcium silicate hydrates gel, and disordered silicon. We show that StriderNET outperforms all classical optimization algorithms and enables the discovery of a lower energy minimum. In addition, StriderNET exhibits a higher rate of reaching minima with energies, as confirmed by the average over multiple realizations. Finally, we show that StriderNET exhibits inductivity to unseen system sizes that are an order of magnitude different from the training system.