CoNO: Complex Neural Operator for Continous Dynamical Physical Systems

Neural operators extend data-driven models to map between infinite-dimensional functional spaces. While these operators perform effectively in either the time or frequency domain, their performance may be limited when applied to non-stationary spatial or temporal signals whose frequency characteristics change with time. Here, we introduce Complex Neural Operator (CoNO) that parameterizes the integral kernel using Fractional Fourier Transform (FrFT), better representing non-stationary signals in a complex-valued domain. Theoretically, we prove the universal approximation capability of CoNO. We perform an extensive empirical evaluation of CoNO on seven challenging partial differential equations (PDEs), including regular grids, structured meshes, and point clouds. Empirically, CoNO consistently attains state-of-the-art performance, showcasing an average relative gain of 10.9%. Further, CoNO exhibits superior performance, outperforming all other models in additional tasks such as zero-shot super-resolution and robustness to noise. CoNO also exhibits the ability to learn from small amounts of data -- giving the same performance as the next best model with just 60% of the training data. Altogether, CoNO presents a robust and superior model for modeling continuous dynamical systems, providing a fillip to scientific machine learning.

Are LLMs Ready for Real-World Materials Discovery?

Large Language Models (LLMs) create exciting possibilities for powerful language processing tools to accelerate research in materials science. While LLMs have great potential to accelerate materials understanding and discovery, they currently fall short in being practical materials science tools. In this position paper, we show relevant failure cases of LLMs in materials science that reveal current limitations of LLMs related to comprehending and reasoning over complex, interconnected materials science knowledge. Given those shortcomings, we outline a framework for developing Materials Science LLMs (MatSci-LLMs) that are grounded in materials science knowledge and hypothesis generation followed by hypothesis testing. The path to attaining performant MatSci-LLMs rests in large part on building high-quality, multi-modal datasets sourced from scientific literature where various information extraction challenges persist. As such, we describe key materials science information extraction challenges which need to be overcome in order to build large-scale, multi-modal datasets that capture valuable materials science knowledge. Finally, we outline a roadmap for applying future MatSci-LLMs for real-world materials discovery via: 1. Automated Knowledge Base Generation; 2. Automated In-Silico Material Design; and 3. MatSci-LLM Integrated Self-Driving Materials Laboratories.

Reconstructing Materials Tetrahedron: Challenges in Materials Information Extraction

Discovery of new materials has a documented history of propelling human progress for centuries and more. The behaviour of a material is a function of its composition, structure, and properties, which further depend on its processing and testing conditions. Recent developments in deep learning and natural language processing have enabled information extraction at scale from published literature such as peer-reviewed publications, books, and patents. However, this information is spread in multiple formats, such as tables, text, and images, and with little or no uniformity in reporting style giving rise to several machine learning challenges. Here, we discuss, quantify, and document these outstanding challenges in automated information extraction (IE) from materials science literature towards the creation of a large materials science knowledge base. Specifically, we focus on IE from text and tables and outline several challenges with examples. We hope the present work inspires researchers to address the challenges in a coherent fashion, providing to fillip to IE for the materials knowledge base.

CoNO: Complex Neural Operator for Continuous Dynamical Systems

Neural operators extend data-driven models to map between infinite-dimensional functional spaces. These models have successfully solved continuous dynamical systems represented by differential equations, viz weather forecasting, fluid flow, or solid mechanics. However, the existing operators still rely on real space, thereby losing rich representations potentially captured in the complex space by functional transforms. In this paper, we introduce a Complex Neural Operator (CoNO), that parameterizes the integral kernel in the complex fractional Fourier domain. Additionally, the model employing a complex-valued neural network along with aliasing-free activation functions preserves the complex values and complex algebraic properties, thereby enabling improved representation, robustness to noise, and generalization. We show that the model effectively captures the underlying partial differential equation with a single complex fractional Fourier transform. We perform an extensive empirical evaluation of CoNO on several datasets and additional tasks such as zero-shot super-resolution, evaluation of out-of-distribution data, data efficiency, and robustness to noise. CoNO exhibits comparable or superior performance to all the state-of-the-art models in these tasks. Altogether, CoNO presents a robust and superior model for modeling continuous dynamical systems, providing a fillip to scientific machine learning.

EGraFFBench: Evaluation of Equivariant Graph Neural Network Force Fields for Atomistic Simulations

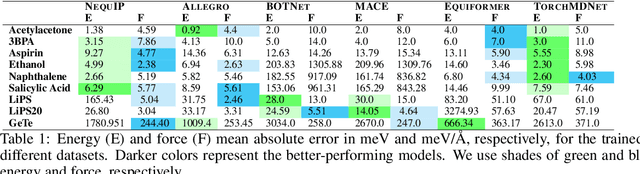
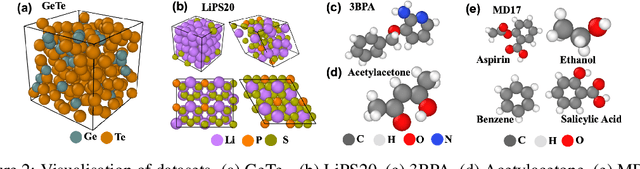
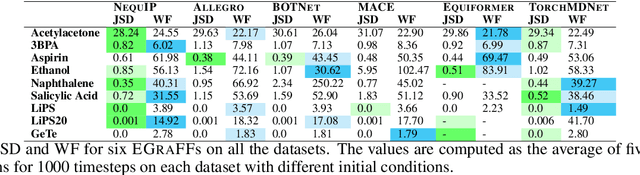
Equivariant graph neural networks force fields (EGraFFs) have shown great promise in modelling complex interactions in atomic systems by exploiting the graphs' inherent symmetries. Recent works have led to a surge in the development of novel architectures that incorporate equivariance-based inductive biases alongside architectural innovations like graph transformers and message passing to model atomic interactions. However, thorough evaluations of these deploying EGraFFs for the downstream task of real-world atomistic simulations, is lacking. To this end, here we perform a systematic benchmarking of 6 EGraFF algorithms (NequIP, Allegro, BOTNet, MACE, Equiformer, TorchMDNet), with the aim of understanding their capabilities and limitations for realistic atomistic simulations. In addition to our thorough evaluation and analysis on eight existing datasets based on the benchmarking literature, we release two new benchmark datasets, propose four new metrics, and three new challenging tasks. The new datasets and tasks evaluate the performance of EGraFF to out-of-distribution data, in terms of different crystal structures, temperatures, and new molecules. Interestingly, evaluation of the EGraFF models based on dynamic simulations reveals that having a lower error on energy or force does not guarantee stable or reliable simulation or faithful replication of the atomic structures. Moreover, we find that no model clearly outperforms other models on all datasets and tasks. Importantly, we show that the performance of all the models on out-of-distribution datasets is unreliable, pointing to the need for the development of a foundation model for force fields that can be used in real-world simulations. In summary, this work establishes a rigorous framework for evaluating machine learning force fields in the context of atomic simulations and points to open research challenges within this domain.

CoDBench: A Critical Evaluation of Data-driven Models for Continuous Dynamical Systems

Continuous dynamical systems, characterized by differential equations, are ubiquitously used to model several important problems: plasma dynamics, flow through porous media, weather forecasting, and epidemic dynamics. Recently, a wide range of data-driven models has been used successfully to model these systems. However, in contrast to established fields like computer vision, limited studies are available analyzing the strengths and potential applications of different classes of these models that could steer decision-making in scientific machine learning. Here, we introduce CodBench, an exhaustive benchmarking suite comprising 11 state-of-the-art data-driven models for solving differential equations. Specifically, we comprehensively evaluate 4 distinct categories of models, viz., feed forward neural networks, deep operator regression models, frequency-based neural operators, and transformer architectures against 8 widely applicable benchmark datasets encompassing challenges from fluid and solid mechanics. We conduct extensive experiments, assessing the operators' capabilities in learning, zero-shot super-resolution, data efficiency, robustness to noise, and computational efficiency. Interestingly, our findings highlight that current operators struggle with the newer mechanics datasets, motivating the need for more robust neural operators. All the datasets and codes will be shared in an easy-to-use fashion for the scientific community. We hope this resource will be an impetus for accelerated progress and exploration in modeling dynamical systems.

Discovering Symbolic Laws Directly from Trajectories with Hamiltonian Graph Neural Networks

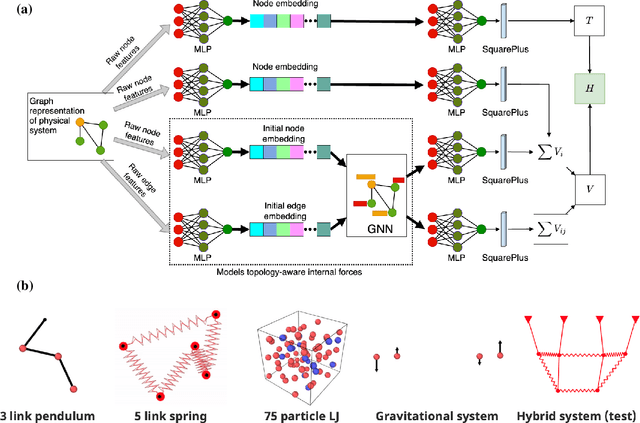
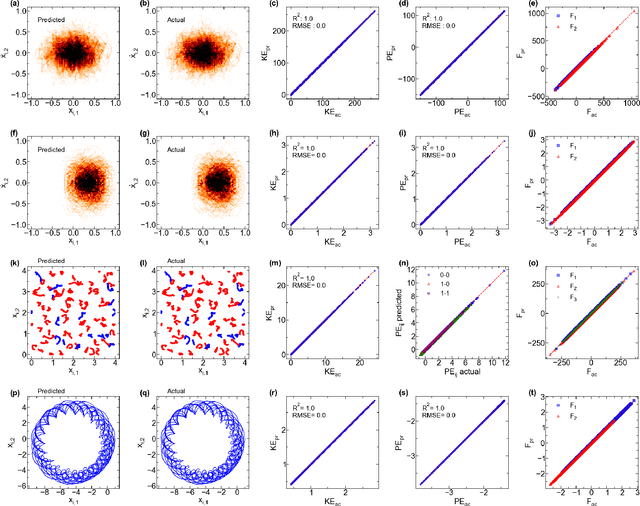
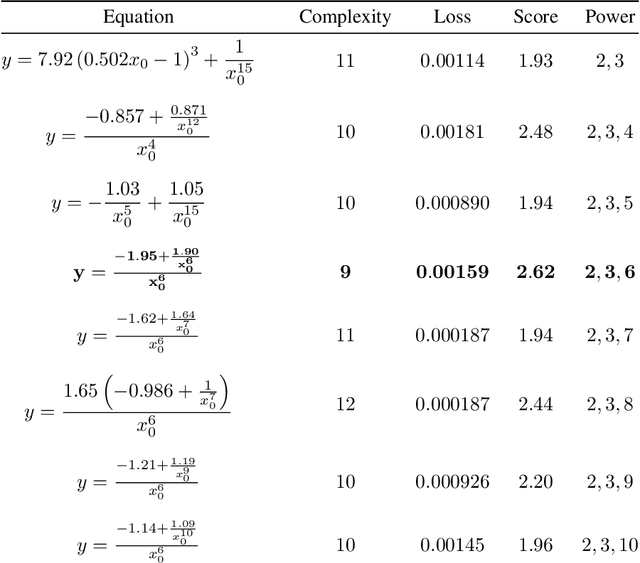
The time evolution of physical systems is described by differential equations, which depend on abstract quantities like energy and force. Traditionally, these quantities are derived as functionals based on observables such as positions and velocities. Discovering these governing symbolic laws is the key to comprehending the interactions in nature. Here, we present a Hamiltonian graph neural network (HGNN), a physics-enforced GNN that learns the dynamics of systems directly from their trajectory. We demonstrate the performance of HGNN on n-springs, n-pendulums, gravitational systems, and binary Lennard Jones systems; HGNN learns the dynamics in excellent agreement with the ground truth from small amounts of data. We also evaluate the ability of HGNN to generalize to larger system sizes, and to hybrid spring-pendulum system that is a combination of two original systems (spring and pendulum) on which the models are trained independently. Finally, employing symbolic regression on the learned HGNN, we infer the underlying equations relating the energy functionals, even for complex systems such as the binary Lennard-Jones liquid. Our framework facilitates the interpretable discovery of interaction laws directly from physical system trajectories. Furthermore, this approach can be extended to other systems with topology-dependent dynamics, such as cells, polydisperse gels, or deformable bodies.

Unravelling the Performance of Physics-informed Graph Neural Networks for Dynamical Systems

Recently, graph neural networks have been gaining a lot of attention to simulate dynamical systems due to their inductive nature leading to zero-shot generalizability. Similarly, physics-informed inductive biases in deep-learning frameworks have been shown to give superior performance in learning the dynamics of physical systems. There is a growing volume of literature that attempts to combine these two approaches. Here, we evaluate the performance of thirteen different graph neural networks, namely, Hamiltonian and Lagrangian graph neural networks, graph neural ODE, and their variants with explicit constraints and different architectures. We briefly explain the theoretical formulation highlighting the similarities and differences in the inductive biases and graph architecture of these systems. We evaluate these models on spring, pendulum, gravitational, and 3D deformable solid systems to compare the performance in terms of rollout error, conserved quantities such as energy and momentum, and generalizability to unseen system sizes. Our study demonstrates that GNNs with additional inductive biases, such as explicit constraints and decoupling of kinetic and potential energies, exhibit significantly enhanced performance. Further, all the physics-informed GNNs exhibit zero-shot generalizability to system sizes an order of magnitude larger than the training system, thus providing a promising route to simulate large-scale realistic systems.