Discovering Symbolic Laws Directly from Trajectories with Hamiltonian Graph Neural Networks

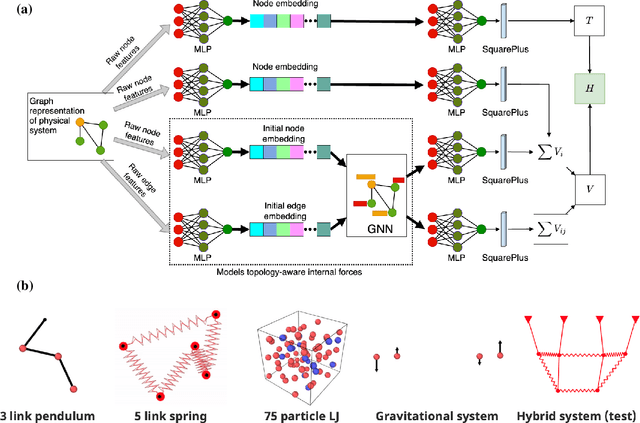
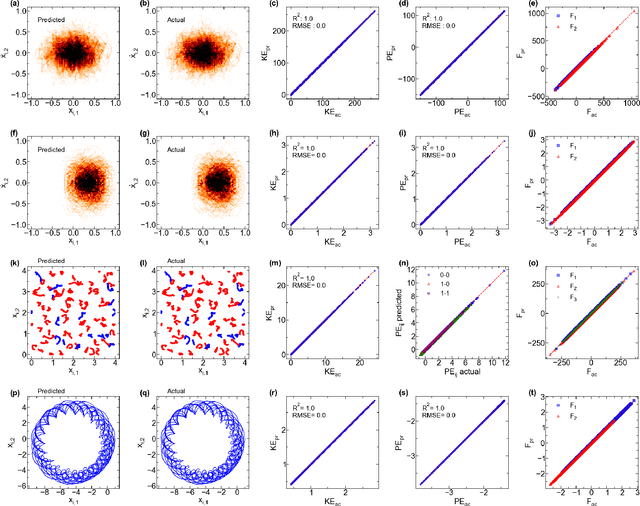
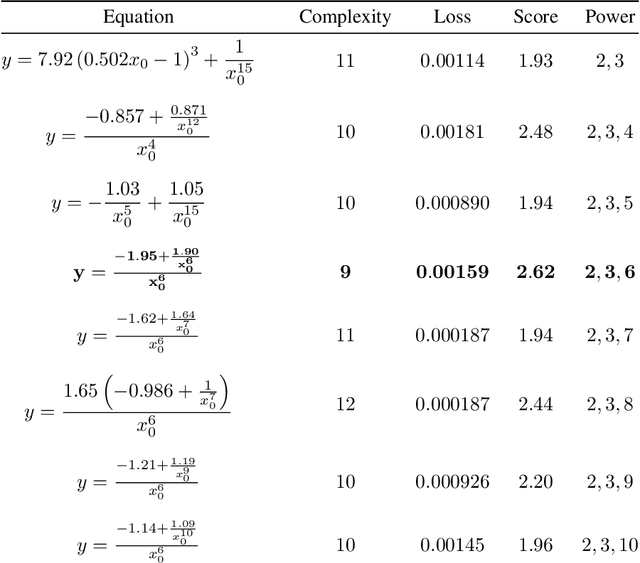
The time evolution of physical systems is described by differential equations, which depend on abstract quantities like energy and force. Traditionally, these quantities are derived as functionals based on observables such as positions and velocities. Discovering these governing symbolic laws is the key to comprehending the interactions in nature. Here, we present a Hamiltonian graph neural network (HGNN), a physics-enforced GNN that learns the dynamics of systems directly from their trajectory. We demonstrate the performance of HGNN on n-springs, n-pendulums, gravitational systems, and binary Lennard Jones systems; HGNN learns the dynamics in excellent agreement with the ground truth from small amounts of data. We also evaluate the ability of HGNN to generalize to larger system sizes, and to hybrid spring-pendulum system that is a combination of two original systems (spring and pendulum) on which the models are trained independently. Finally, employing symbolic regression on the learned HGNN, we infer the underlying equations relating the energy functionals, even for complex systems such as the binary Lennard-Jones liquid. Our framework facilitates the interpretable discovery of interaction laws directly from physical system trajectories. Furthermore, this approach can be extended to other systems with topology-dependent dynamics, such as cells, polydisperse gels, or deformable bodies.