NeuroCUT: A Neural Approach for Robust Graph Partitioning
Paper and Code
Oct 18, 2023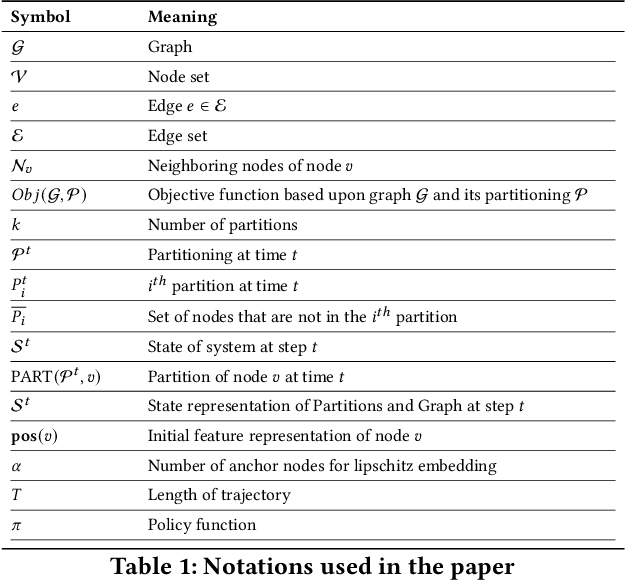
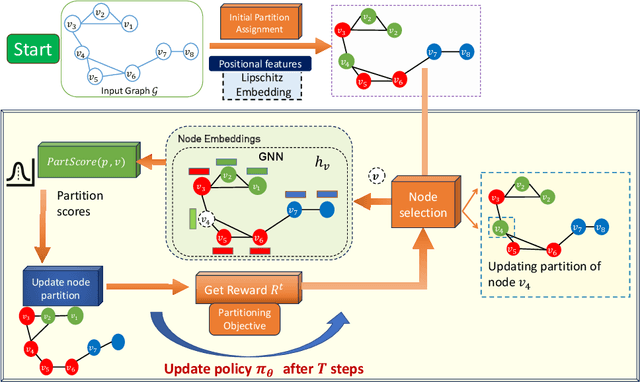
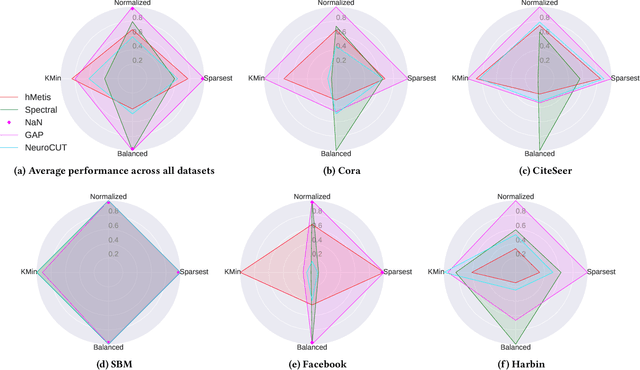
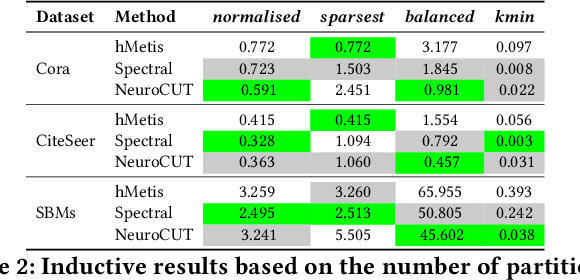
Graph partitioning aims to divide a graph into $k$ disjoint subsets while optimizing a specific partitioning objective. The majority of formulations related to graph partitioning exhibit NP-hardness due to their combinatorial nature. As a result, conventional approximation algorithms rely on heuristic methods, sometimes with approximation guarantees and sometimes without. Unfortunately, traditional approaches are tailored for specific partitioning objectives and do not generalize well across other known partitioning objectives from the literature. To overcome this limitation, and learn heuristics from the data directly, neural approaches have emerged, demonstrating promising outcomes. In this study, we extend this line of work through a novel framework, NeuroCut. NeuroCut introduces two key innovations over prevailing methodologies. First, it is inductive to both graph topology and the partition count, which is provided at query time. Second, by leveraging a reinforcement learning based framework over node representations derived from a graph neural network, NeuroCut can accommodate any optimization objective, even those encompassing non-differentiable functions. Through empirical evaluation, we demonstrate that NeuroCut excels in identifying high-quality partitions, showcases strong generalization across a wide spectrum of partitioning objectives, and exhibits resilience to topological modifications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge