Diverging Towards Hallucination: Detection of Failures in Vision-Language Models via Multi-token Aggregation

Vision-language models (VLMs) now rival human performance on many multimodal tasks, yet they still hallucinate objects or generate unsafe text. Current hallucination detectors, e.g., single-token linear probing (SLP) and P(True), typically analyze only the logit of the first generated token or just its highest scoring component overlooking richer signals embedded within earlier token distributions. We demonstrate that analyzing the complete sequence of early logits potentially provides substantially more diagnostic information. We emphasize that hallucinations may only emerge after several tokens, as subtle inconsistencies accumulate over time. By analyzing the Kullback-Leibler (KL) divergence between logits corresponding to hallucinated and non-hallucinated tokens, we underscore the importance of incorporating later-token logits to more accurately capture the reliability dynamics of VLMs. In response, we introduce Multi-Token Reliability Estimation (MTRE), a lightweight, white-box method that aggregates logits from the first ten tokens using multi-token log-likelihood ratios and self-attention. Despite the challenges posed by large vocabulary sizes and long logit sequences, MTRE remains efficient and tractable. On MAD-Bench, MM-SafetyBench, MathVista, and four compositional-geometry benchmarks, MTRE improves AUROC by 9.4 +/- 1.3 points over SLP and by 12.1 +/- 1.7 points over P(True), setting a new state-of-the-art in hallucination detection for open-source VLMs.

Topological Signatures of Adversaries in Multimodal Alignments

Multimodal Machine Learning systems, particularly those aligning text and image data like CLIP/BLIP models, have become increasingly prevalent, yet remain susceptible to adversarial attacks. While substantial research has addressed adversarial robustness in unimodal contexts, defense strategies for multimodal systems are underexplored. This work investigates the topological signatures that arise between image and text embeddings and shows how adversarial attacks disrupt their alignment, introducing distinctive signatures. We specifically leverage persistent homology and introduce two novel Topological-Contrastive losses based on Total Persistence and Multi-scale kernel methods to analyze the topological signatures introduced by adversarial perturbations. We observe a pattern of monotonic changes in the proposed topological losses emerging in a wide range of attacks on image-text alignments, as more adversarial samples are introduced in the data. By designing an algorithm to back-propagate these signatures to input samples, we are able to integrate these signatures into Maximum Mean Discrepancy tests, creating a novel class of tests that leverage topological signatures for better adversarial detection.

FedEFM: Federated Endovascular Foundation Model with Unseen Data

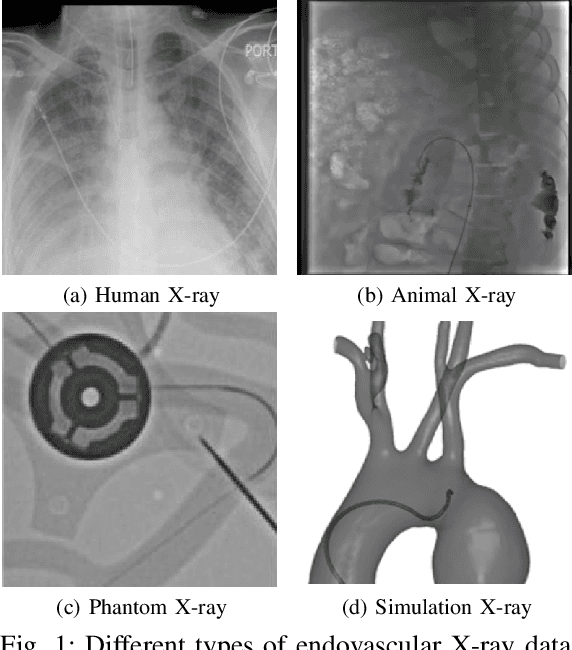
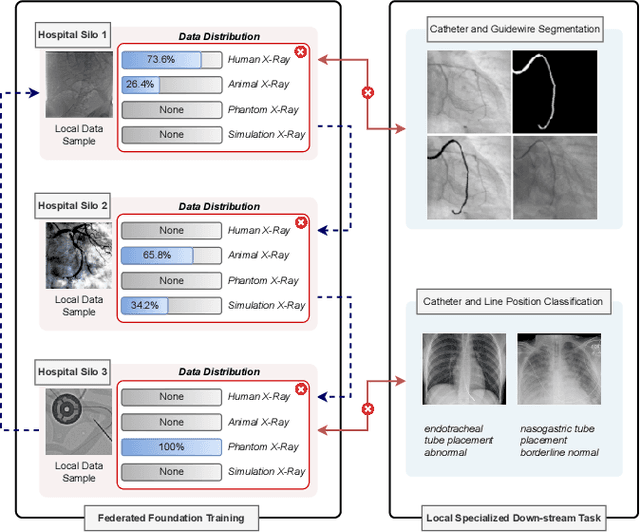
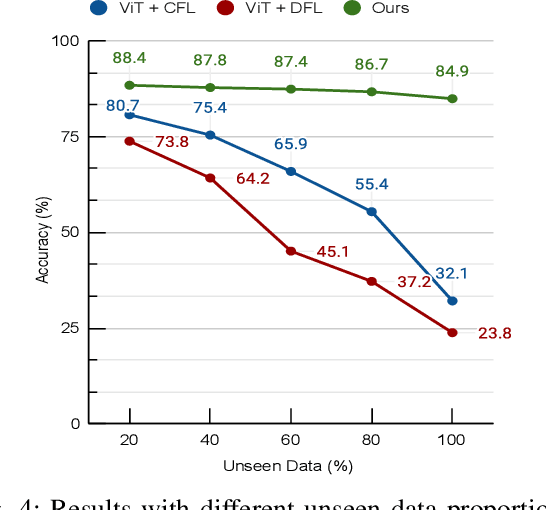
In endovascular surgery, the precise identification of catheters and guidewires in X-ray images is essential for reducing intervention risks. However, accurately segmenting catheter and guidewire structures is challenging due to the limited availability of labeled data. Foundation models offer a promising solution by enabling the collection of similar domain data to train models whose weights can be fine-tuned for downstream tasks. Nonetheless, large-scale data collection for training is constrained by the necessity of maintaining patient privacy. This paper proposes a new method to train a foundation model in a decentralized federated learning setting for endovascular intervention. To ensure the feasibility of the training, we tackle the unseen data issue using differentiable Earth Mover's Distance within a knowledge distillation framework. Once trained, our foundation model's weights provide valuable initialization for downstream tasks, thereby enhancing task-specific performance. Intensive experiments show that our approach achieves new state-of-the-art results, contributing to advancements in endovascular intervention and robotic-assisted endovascular surgery, while addressing the critical issue of data sharing in the medical domain.

Enhancing Cross-Language Code Translation via Task-Specific Embedding Alignment in Retrieval-Augmented Generation

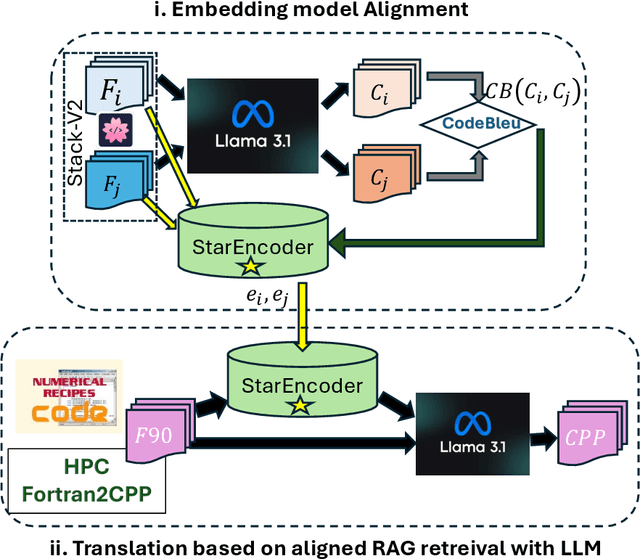
We introduce a novel method to enhance cross-language code translation from Fortran to C++ by integrating task-specific embedding alignment into a Retrieval-Augmented Generation (RAG) framework. Unlike conventional retrieval approaches that utilize generic embeddings agnostic to the downstream task, our strategy aligns the retrieval model directly with the objective of maximizing translation quality, as quantified by the CodeBLEU metric. This alignment ensures that the embeddings are semantically and syntactically meaningful for the specific code translation task. Our methodology involves constructing a dataset of 25,000 Fortran code snippets sourced from Stack-V2 dataset and generating their corresponding C++ translations using the LLaMA 3.1-8B language model. We compute pairwise CodeBLEU scores between the generated translations and ground truth examples to capture fine-grained similarities. These scores serve as supervision signals in a contrastive learning framework, where we optimize the embedding model to retrieve Fortran-C++ pairs that are most beneficial for improving the language model's translation performance. By integrating these CodeBLEU-optimized embeddings into the RAG framework, our approach significantly enhances both retrieval accuracy and code generation quality over methods employing generic embeddings. On the HPC Fortran2C++ dataset, our method elevates the average CodeBLEU score from 0.64 to 0.73, achieving a 14% relative improvement. On the Numerical Recipes dataset, we observe an increase from 0.52 to 0.60, marking a 15% relative improvement. Importantly, these gains are realized without any fine-tuning of the language model, underscoring the efficiency and practicality of our approach.

HEAL: Hierarchical Embedding Alignment Loss for Improved Retrieval and Representation Learning

Retrieval-Augmented Generation (RAG) enhances Large Language Models (LLMs) by integrating external document retrieval to provide domain-specific or up-to-date knowledge. The effectiveness of RAG depends on the relevance of retrieved documents, which is influenced by the semantic alignment of embeddings with the domain's specialized content. Although full fine-tuning can align language models to specific domains, it is computationally intensive and demands substantial data. This paper introduces Hierarchical Embedding Alignment Loss (HEAL), a novel method that leverages hierarchical fuzzy clustering with matrix factorization within contrastive learning to efficiently align LLM embeddings with domain-specific content. HEAL computes level/depth-wise contrastive losses and incorporates hierarchical penalties to align embeddings with the underlying relationships in label hierarchies. This approach enhances retrieval relevance and document classification, effectively reducing hallucinations in LLM outputs. In our experiments, we benchmark and evaluate HEAL across diverse domains, including Healthcare, Material Science, Cyber-security, and Applied Maths.

Patchfinder: Leveraging Visual Language Models for Accurate Information Retrieval using Model Uncertainty

For decades, corporations and governments have relied on scanned documents to record vast amounts of information. However, extracting this information is a slow and tedious process due to the overwhelming amount of documents. The rise of vision language models presents a way to efficiently and accurately extract the information out of these documents. The current automated workflow often requires a two-step approach involving the extraction of information using optical character recognition software, and subsequent usage of large language models for processing this information. Unfortunately, these methods encounter significant challenges when dealing with noisy scanned documents. The high information density of such documents often necessitates using computationally expensive language models to effectively reduce noise. In this study, we propose PatchFinder, an algorithm that builds upon Vision Language Models (VLMs) to address the information extraction task. First, we devise a confidence-based score, called Patch Confidence, based on the Maximum Softmax Probability of the VLMs' output to measure the model's confidence in its predictions. Then, PatchFinder utilizes that score to determine a suitable patch size, partition the input document into overlapping patches of that size, and generate confidence-based predictions for the target information. Our experimental results show that PatchFinder can leverage Phi-3v, a 4.2 billion parameter vision language model, to achieve an accuracy of 94% on our dataset of 190 noisy scanned documents, surpassing the performance of ChatGPT-4o by 18.5 percentage points.

LoRID: Low-Rank Iterative Diffusion for Adversarial Purification

This work presents an information-theoretic examination of diffusion-based purification methods, the state-of-the-art adversarial defenses that utilize diffusion models to remove malicious perturbations in adversarial examples. By theoretically characterizing the inherent purification errors associated with the Markov-based diffusion purifications, we introduce LoRID, a novel Low-Rank Iterative Diffusion purification method designed to remove adversarial perturbation with low intrinsic purification errors. LoRID centers around a multi-stage purification process that leverages multiple rounds of diffusion-denoising loops at the early time-steps of the diffusion models, and the integration of Tucker decomposition, an extension of matrix factorization, to remove adversarial noise at high-noise regimes. Consequently, LoRID increases the effective diffusion time-steps and overcomes strong adversarial attacks, achieving superior robustness performance in CIFAR-10/100, CelebA-HQ, and ImageNet datasets under both white-box and black-box settings.

Gaussian-Mixture-Model Q-Functions for Reinforcement Learning by Riemannian Optimization

This paper establishes a novel role for Gaussian-mixture models (GMMs) as functional approximators of Q-function losses in reinforcement learning (RL). Unlike the existing RL literature, where GMMs play their typical role as estimates of probability density functions, GMMs approximate here Q-function losses. The new Q-function approximators, coined GMM-QFs, are incorporated in Bellman residuals to promote a Riemannian-optimization task as a novel policy-evaluation step in standard policy-iteration schemes. The paper demonstrates how the hyperparameters (means and covariance matrices) of the Gaussian kernels are learned from the data, opening thus the door of RL to the powerful toolbox of Riemannian optimization. Numerical tests show that with no use of experienced data, the proposed design outperforms state-of-the-art methods, even deep Q-networks which use experienced data, on benchmark RL tasks.

CathAction: A Benchmark for Endovascular Intervention Understanding

Real-time visual feedback from catheterization analysis is crucial for enhancing surgical safety and efficiency during endovascular interventions. However, existing datasets are often limited to specific tasks, small scale, and lack the comprehensive annotations necessary for broader endovascular intervention understanding. To tackle these limitations, we introduce CathAction, a large-scale dataset for catheterization understanding. Our CathAction dataset encompasses approximately 500,000 annotated frames for catheterization action understanding and collision detection, and 25,000 ground truth masks for catheter and guidewire segmentation. For each task, we benchmark recent related works in the field. We further discuss the challenges of endovascular intentions compared to traditional computer vision tasks and point out open research questions. We hope that CathAction will facilitate the development of endovascular intervention understanding methods that can be applied to real-world applications. The dataset is available at https://airvlab.github.io/cathdata/.

LaFA: Latent Feature Attacks on Non-negative Matrix Factorization

As Machine Learning (ML) applications rapidly grow, concerns about adversarial attacks compromising their reliability have gained significant attention. One unsupervised ML method known for its resilience to such attacks is Non-negative Matrix Factorization (NMF), an algorithm that decomposes input data into lower-dimensional latent features. However, the introduction of powerful computational tools such as Pytorch enables the computation of gradients of the latent features with respect to the original data, raising concerns about NMF's reliability. Interestingly, naively deriving the adversarial loss for NMF as in the case of ML would result in the reconstruction loss, which can be shown theoretically to be an ineffective attacking objective. In this work, we introduce a novel class of attacks in NMF termed Latent Feature Attacks (LaFA), which aim to manipulate the latent features produced by the NMF process. Our method utilizes the Feature Error (FE) loss directly on the latent features. By employing FE loss, we generate perturbations in the original data that significantly affect the extracted latent features, revealing vulnerabilities akin to those found in other ML techniques. To handle large peak-memory overhead from gradient back-propagation in FE attacks, we develop a method based on implicit differentiation which enables their scaling to larger datasets. We validate NMF vulnerabilities and FE attacks effectiveness through extensive experiments on synthetic and real-world data.