LaFA: Latent Feature Attacks on Non-negative Matrix Factorization

As Machine Learning (ML) applications rapidly grow, concerns about adversarial attacks compromising their reliability have gained significant attention. One unsupervised ML method known for its resilience to such attacks is Non-negative Matrix Factorization (NMF), an algorithm that decomposes input data into lower-dimensional latent features. However, the introduction of powerful computational tools such as Pytorch enables the computation of gradients of the latent features with respect to the original data, raising concerns about NMF's reliability. Interestingly, naively deriving the adversarial loss for NMF as in the case of ML would result in the reconstruction loss, which can be shown theoretically to be an ineffective attacking objective. In this work, we introduce a novel class of attacks in NMF termed Latent Feature Attacks (LaFA), which aim to manipulate the latent features produced by the NMF process. Our method utilizes the Feature Error (FE) loss directly on the latent features. By employing FE loss, we generate perturbations in the original data that significantly affect the extracted latent features, revealing vulnerabilities akin to those found in other ML techniques. To handle large peak-memory overhead from gradient back-propagation in FE attacks, we develop a method based on implicit differentiation which enables their scaling to larger datasets. We validate NMF vulnerabilities and FE attacks effectiveness through extensive experiments on synthetic and real-world data.

Process Modeling, Hidden Markov Models, and Non-negative Tensor Factorization with Model Selection

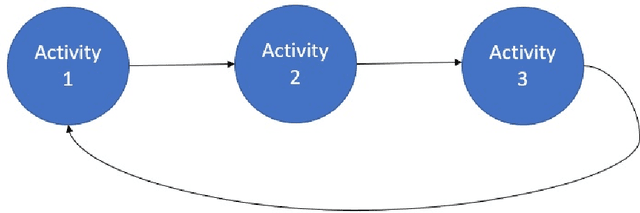
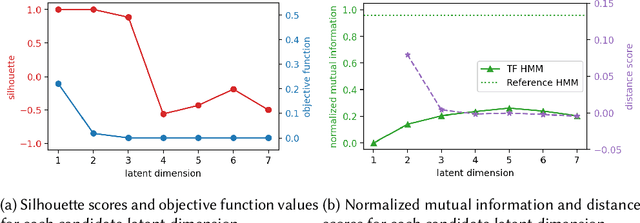
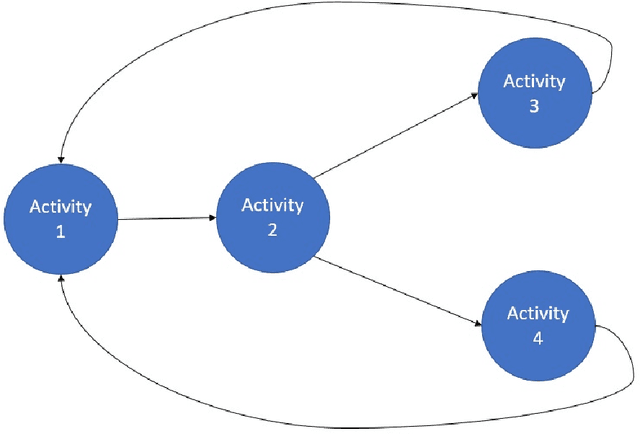
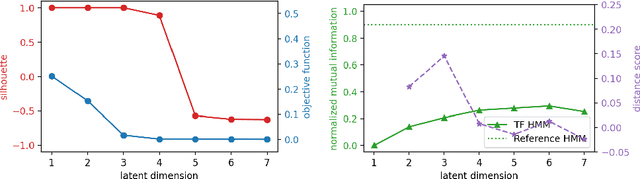
Monitoring of industrial processes is a critical capability in industry and in government to ensure reliability of production cycles, quick emergency response, and national security. Process monitoring allows users to gauge the involvement of an organization in an industrial process or predict the degradation or aging of machine parts in processes taking place at a remote location. Similar to many data science applications, we usually only have access to limited raw data, such as satellite imagery, short video clips, some event logs, and signatures captured by a small set of sensors. To combat data scarcity, we leverage the knowledge of subject matter experts (SMEs) who are familiar with the process. Various process mining techniques have been developed for this type of analysis; typically such approaches combine theoretical process models built based on domain expert insights with ad-hoc integration of available pieces of raw data. Here, we introduce a novel mathematically sound method that integrates theoretical process models (as proposed by SMEs) with interrelated minimal Hidden Markov Models (HMM), built via non-negative tensor factorization and discrete model simulations. Our method consolidates: (a) Theoretical process models development, (b) Discrete model simulations (c) HMM, (d) Joint Non-negative Matrix Factorization (NMF) and Non-negative Tensor Factorization (NTF), and (e) Custom model selection. To demonstrate our methodology and its abilities, we apply it on simple synthetic and real world process models.

Distributed Out-of-Memory NMF of Dense and Sparse Data on CPU/GPU Architectures with Automatic Model Selection for Exascale Data

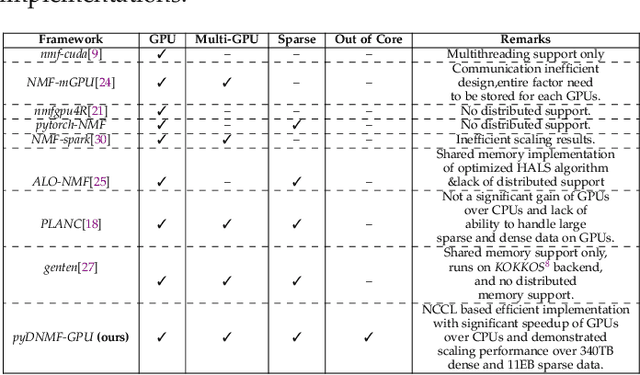
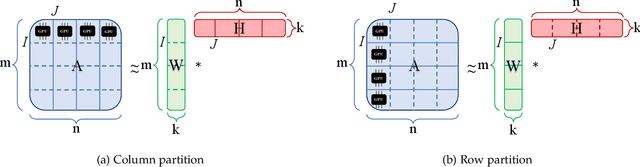
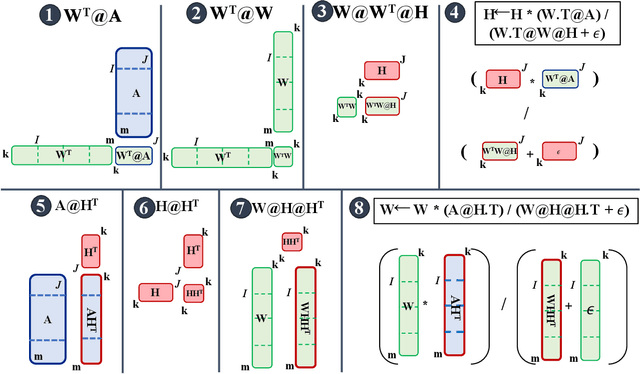
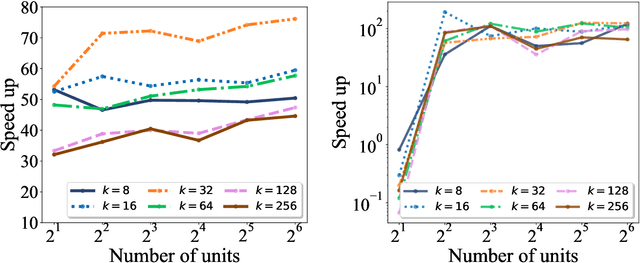
The need for efficient and scalable big-data analytics methods is more essential than ever due to the exploding size and complexity of globally emerging datasets. Nonnegative Matrix Factorization (NMF) is a well-known explainable unsupervised learning method for dimensionality reduction, latent feature extraction, blind source separation, data mining, and machine learning. In this paper, we introduce a new distributed out-of-memory NMF method, named pyDNMF-GPU, designed for modern heterogeneous CPU/GPU architectures that is capable of factoring exascale-sized dense and sparse matrices. Our method reduces the latency associated with local data transfer between the GPU and host using CUDA streams, and reduces the latency associated with collective communications (both intra-node and inter-node) via NCCL primitives. In addition, sparse and dense matrix multiplications are significantly accelerated with GPU cores, resulting in good scalability. We set new benchmarks for the size of the data being analyzed: in experiments, we measure up to 76x improvement on a single GPU over running on a single 18 core CPU and we show good weak scaling on up to 4096 multi-GPU cluster nodes with approximately 25,000 GPUs, when decomposing a dense 340 Terabyte-size matrix and a 11 Exabyte-size sparse matrix of density 10e-6. Finally, we integrate our method with an automatic model selection method. With this integration, we introduce a new tool that is capable of analyzing, compressing, and discovering explainable latent structures in extremely large sparse and dense data.

Topic Analysis of Superconductivity Literature by Semantic Non-negative Matrix Factorization

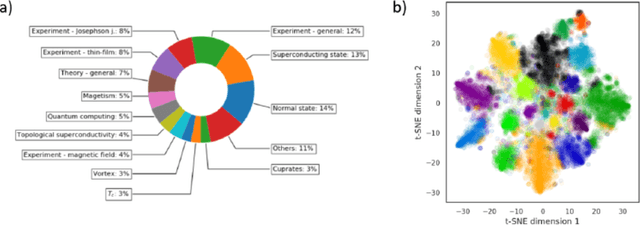
We utilize a recently developed topic modeling method called SeNMFk, extending the standard Non-negative Matrix Factorization (NMF) methods by incorporating the semantic structure of the text, and adding a robust system for determining the number of topics. With SeNMFk, we were able to extract coherent topics validated by human experts. From these topics, a few are relatively general and cover broad concepts, while the majority can be precisely mapped to specific scientific effects or measurement techniques. The topics also differ by ubiquity, with only three topics prevalent in almost 40 percent of the abstract, while each specific topic tends to dominate a small subset of the abstracts. These results demonstrate the ability of SeNMFk to produce a layered and nuanced analysis of large scientific corpora.

Boolean Matrix Factorization via Nonnegative Auxiliary Optimization

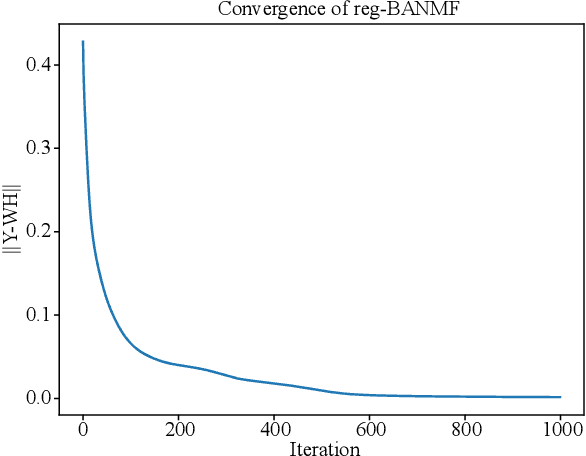
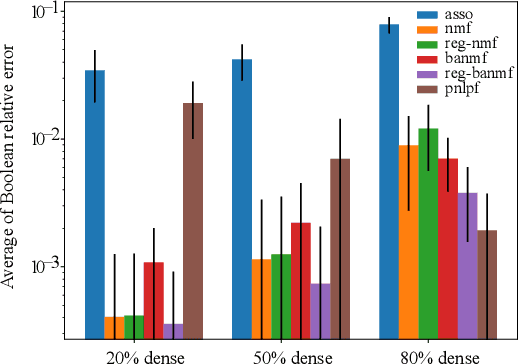
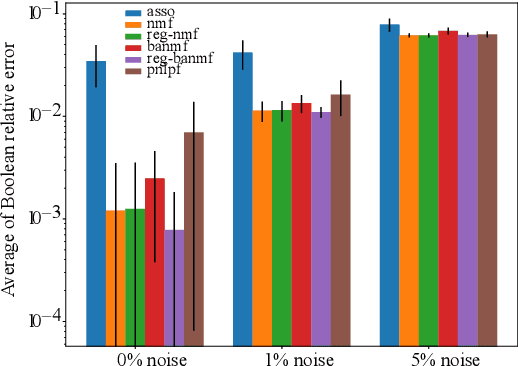
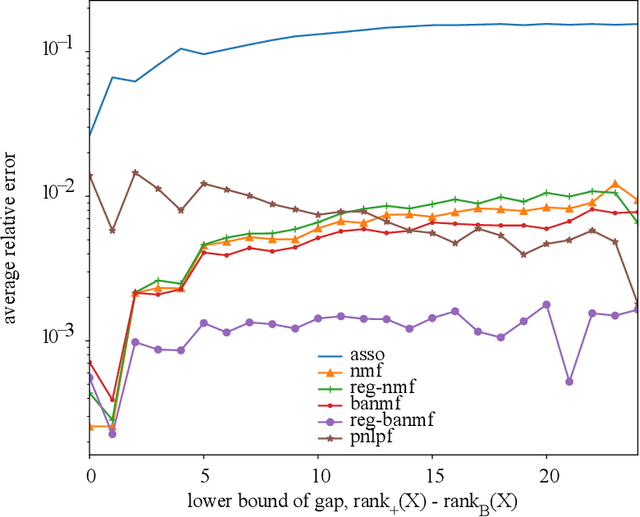
A novel approach to Boolean matrix factorization (BMF) is presented. Instead of solving the BMF problem directly, this approach solves a nonnegative optimization problem with the constraint over an auxiliary matrix whose Boolean structure is identical to the initial Boolean data. Then the solution of the nonnegative auxiliary optimization problem is thresholded to provide a solution for the BMF problem. We provide the proofs for the equivalencies of the two solution spaces under the existence of an exact solution. Moreover, the nonincreasing property of the algorithm is also proven. Experiments on synthetic and real datasets are conducted to show the effectiveness and complexity of the algorithm compared to other current methods.

Distributed Non-Negative Tensor Train Decomposition

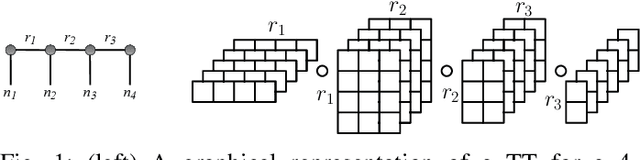
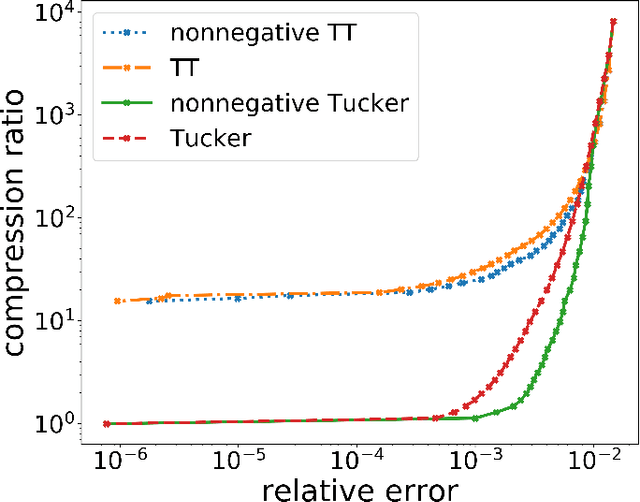
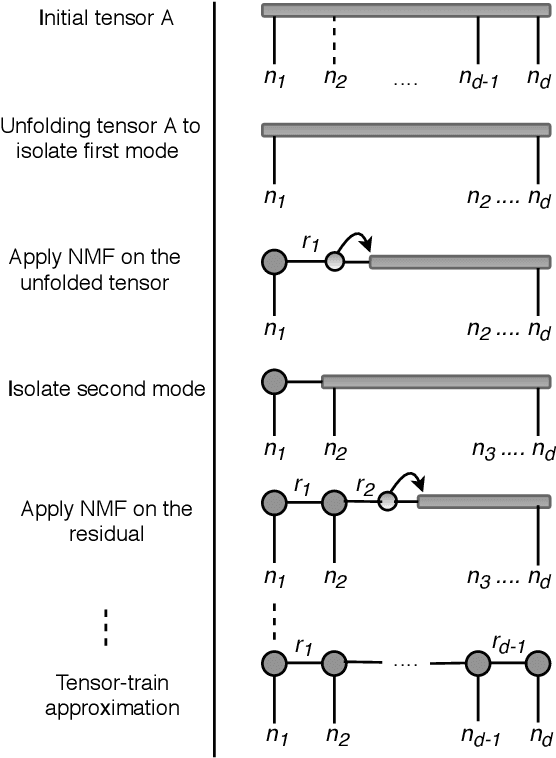
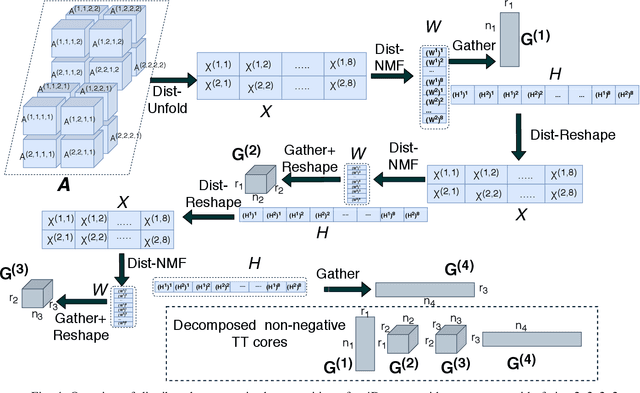
The era of exascale computing opens new venues for innovations and discoveries in many scientific, engineering, and commercial fields. However, with the exaflops also come the extra-large high-dimensional data generated by high-performance computing. High-dimensional data is presented as multidimensional arrays, aka tensors. The presence of latent (not directly observable) structures in the tensor allows a unique representation and compression of the data by classical tensor factorization techniques. However, the classical tensor methods are not always stable or they can be exponential in their memory requirements, which makes them not suitable for high-dimensional tensors. Tensor train (TT) is a state-of-the-art tensor network introduced for factorization of high-dimensional tensors. TT transforms the initial high-dimensional tensor in a network of three-dimensional tensors that requires only a linear storage. Many real-world data, such as, density, temperature, population, probability, etc., are non-negative and for an easy interpretation, the algorithms preserving non-negativity are preferred. Here, we introduce a distributed non-negative tensor-train and demonstrate its scalability and the compression on synthetic and real-world big datasets.

Determination of Latent Dimensionality in International Trade Flow

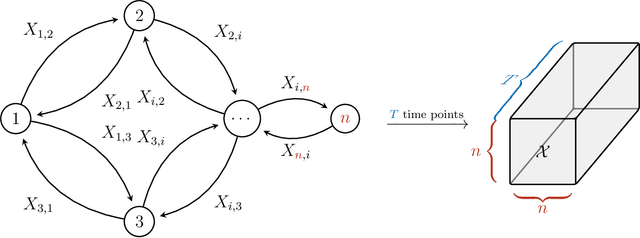
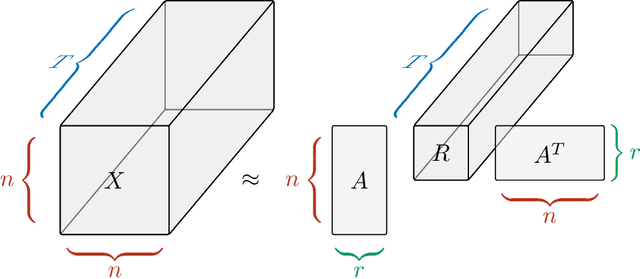
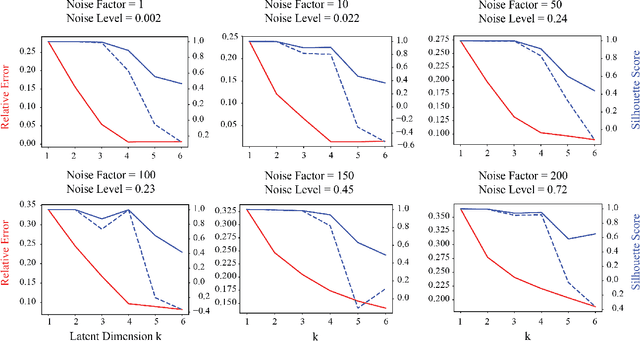
Currently, high-dimensional data is ubiquitous in data science, which necessitates the development of techniques to decompose and interpret such multidimensional (aka tensor) datasets. Finding a low dimensional representation of the data, that is, its inherent structure, is one of the approaches that can serve to understand the dynamics of low dimensional latent features hidden in the data. Nonnegative RESCAL is one such technique, particularly well suited to analyze self-relational data, such as dynamic networks found in international trade flows. Nonnegative RESCAL computes a low dimensional tensor representation by finding the latent space containing multiple modalities. Estimating the dimensionality of this latent space is crucial for extracting meaningful latent features. Here, to determine the dimensionality of the latent space with nonnegative RESCAL, we propose a latent dimension determination method which is based on clustering of the solutions of multiple realizations of nonnegative RESCAL decompositions. We demonstrate the performance of our model selection method on synthetic data and then we apply our method to decompose a network of international trade flows data from International Monetary Fund and validate the resulting features against empirical facts from economic literature.