Identification of Anomalous Diffusion Sources by Unsupervised Learning

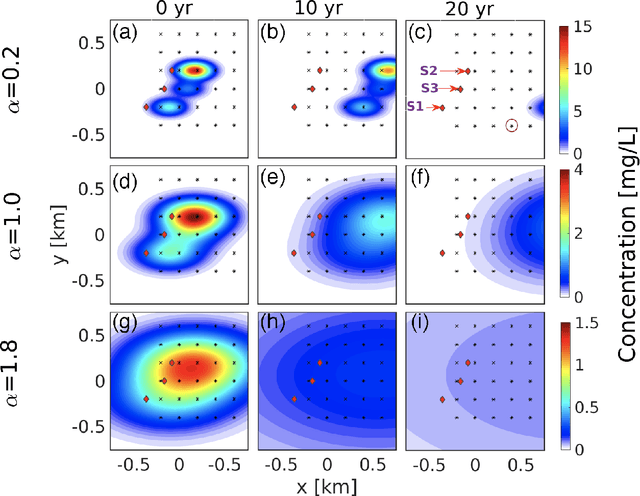
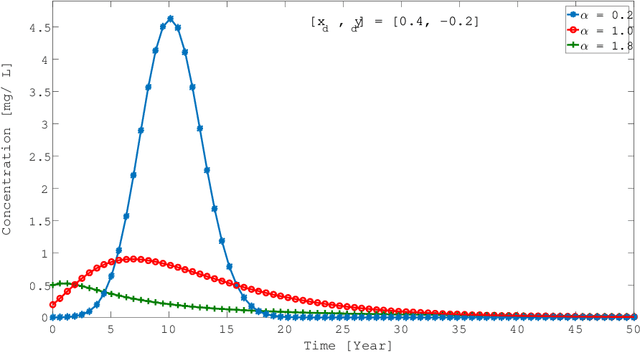
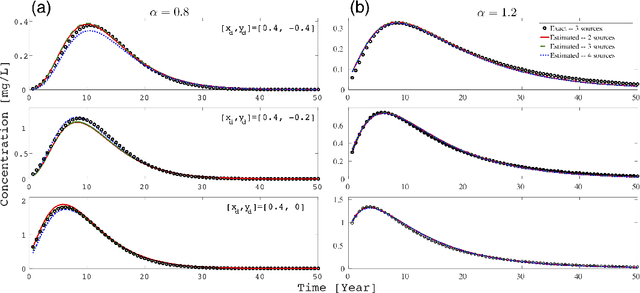
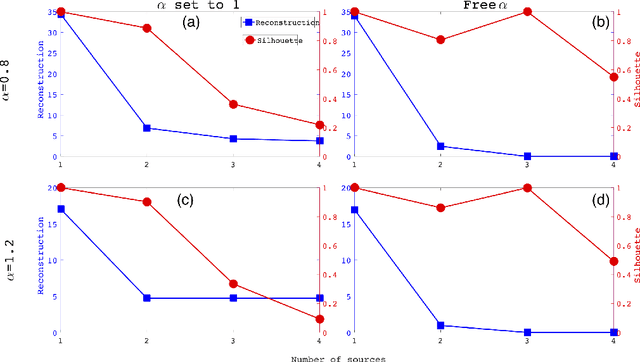
Fractional Brownian motion (fBm) is a ubiquitous diffusion process in which the memory effects of the stochastic transport result in the mean squared particle displacement following a power law, $\langle {\Delta r}^2 \rangle \sim t^{\alpha}$, where the diffusion exponent $\alpha$ characterizes whether the transport is subdiffusive, ($\alpha<1$), diffusive ($\alpha = 1$), or superdiffusive, ($\alpha >1$). Due to the abundance of fBm processes in nature, significant efforts have been devoted to the identification and characterization of fBm sources in various phenomena. In practice, the identification of the fBm sources often relies on solving a complex and ill-posed inverse problem based on limited observed data. In the general case, the detected signals are formed by an unknown number of release sources, located at different locations and with different strengths, that act simultaneously. This means that the observed data is composed of mixtures of releases from an unknown number of sources, which makes the traditional inverse modeling approaches unreliable. Here, we report an unsupervised learning method, based on Nonnegative Matrix Factorization, that enables the identification of the unknown number of release sources as well the anomalous diffusion characteristics based on limited observed data and the general form of the corresponding fBm Green's function. We show that our method performs accurately for different types of sources and configurations with a predetermined number of sources with specific characteristics and introduced noise.

Distributed Non-Negative Tensor Train Decomposition

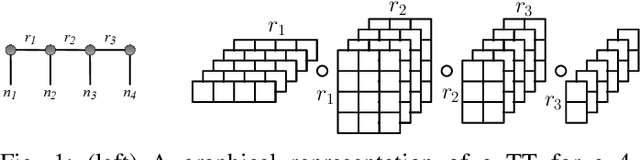
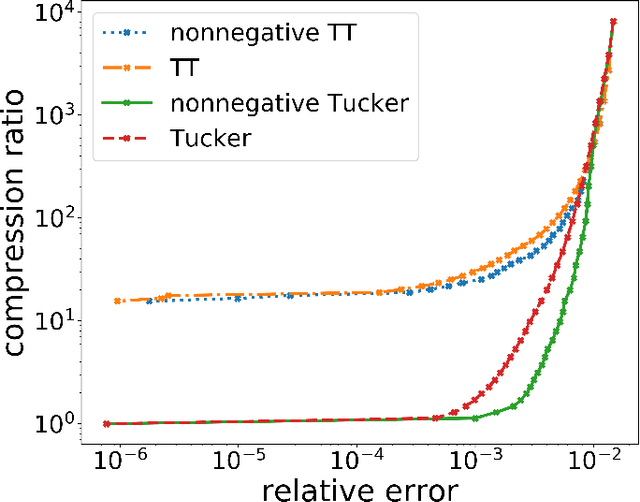
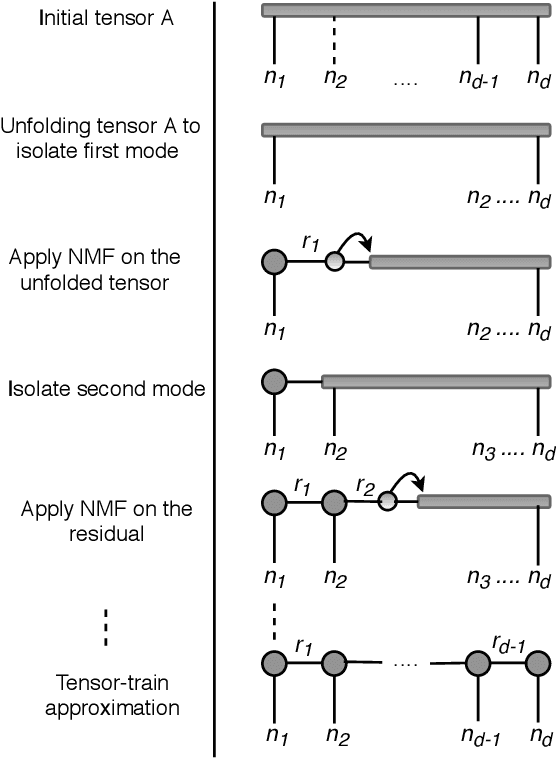
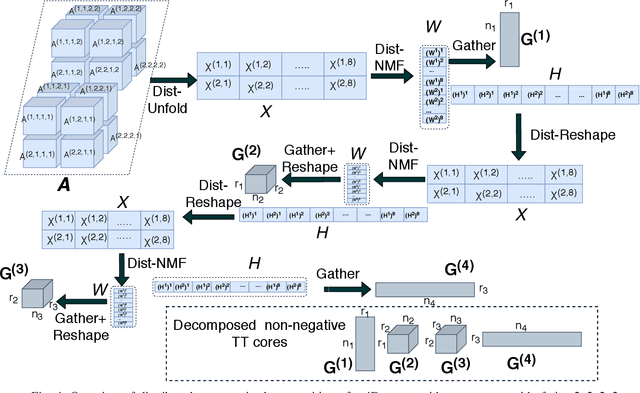
The era of exascale computing opens new venues for innovations and discoveries in many scientific, engineering, and commercial fields. However, with the exaflops also come the extra-large high-dimensional data generated by high-performance computing. High-dimensional data is presented as multidimensional arrays, aka tensors. The presence of latent (not directly observable) structures in the tensor allows a unique representation and compression of the data by classical tensor factorization techniques. However, the classical tensor methods are not always stable or they can be exponential in their memory requirements, which makes them not suitable for high-dimensional tensors. Tensor train (TT) is a state-of-the-art tensor network introduced for factorization of high-dimensional tensors. TT transforms the initial high-dimensional tensor in a network of three-dimensional tensors that requires only a linear storage. Many real-world data, such as, density, temperature, population, probability, etc., are non-negative and for an easy interpretation, the algorithms preserving non-negativity are preferred. Here, we introduce a distributed non-negative tensor-train and demonstrate its scalability and the compression on synthetic and real-world big datasets.

A Neural Network for Determination of Latent Dimensionality in Nonnegative Matrix Factorization

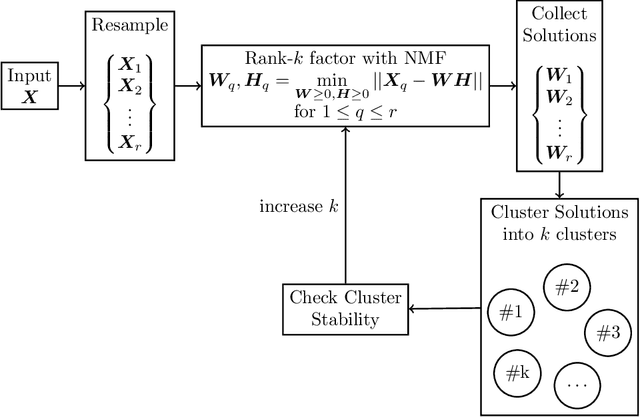
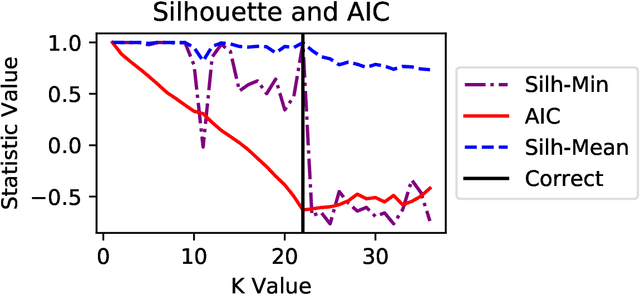
Non-negative Matrix Factorization (NMF) has proven to be a powerful unsupervised learning method for uncovering hidden features in complex and noisy data sets with applications in data mining, text recognition, dimension reduction, face recognition, anomaly detection, blind source separation, and many other fields. An important input for NMF is the latent dimensionality of the data, that is, the number of hidden features, K, present in the explored data set. Unfortunately, this quantity is rarely known a priori. We utilize a supervised machine learning approach in combination with a recent method for model determination, called NMFk, to determine the number of hidden features automatically. NMFk performs a set of NMF simulations on an ensemble of matrices, obtained by bootstrapping the initial data set, and determines which K produces stable groups of latent features that reconstruct the initial data set well. We then train a Multi-Layer Perceptron (MLP) classifier network to determine the correct number of latent features utilizing the statistics and characteristics of the NMF solutions, obtained from NMFk. In order to train the MLP classifier, a training set of 58,660 matrices with predetermined latent features were factorized with NMFk. The MLP classifier in conjunction with NMFk maintains a greater than 95% success rate when applied to a held out test set. Additionally, when applied to two well-known benchmark data sets, the swimmer and MIT face data, NMFk/MLP correctly recovered the established number of hidden features. Finally, we compared the accuracy of our method to the ARD, AIC and Stability-based methods.