Golan Bel
Identification of Anomalous Diffusion Sources by Unsupervised Learning
Oct 05, 2020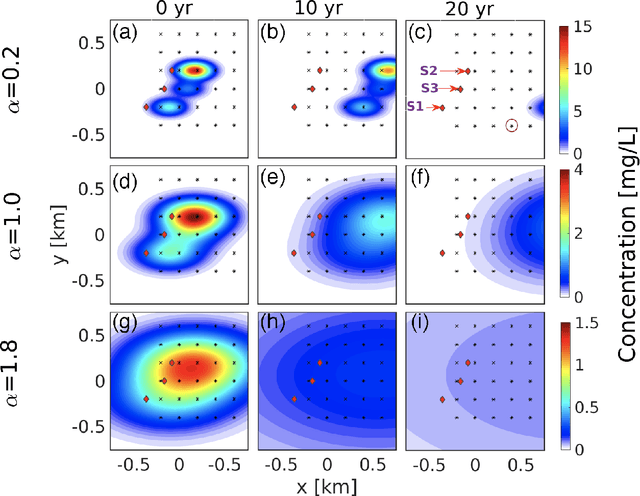
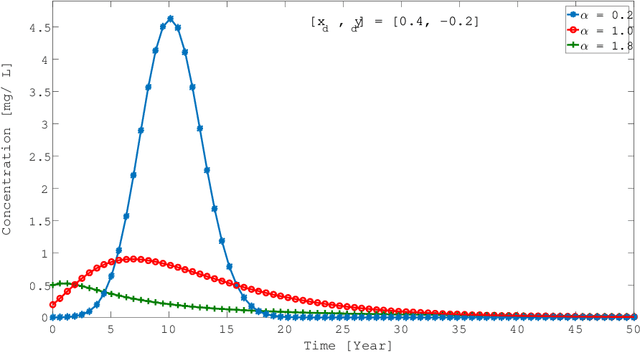
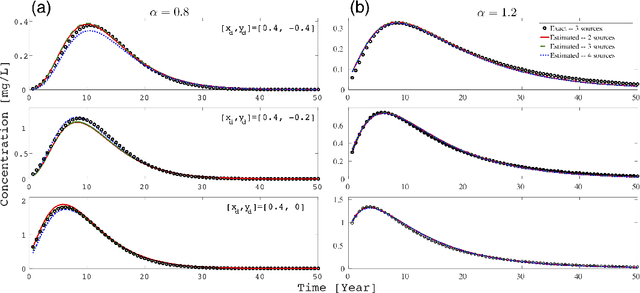
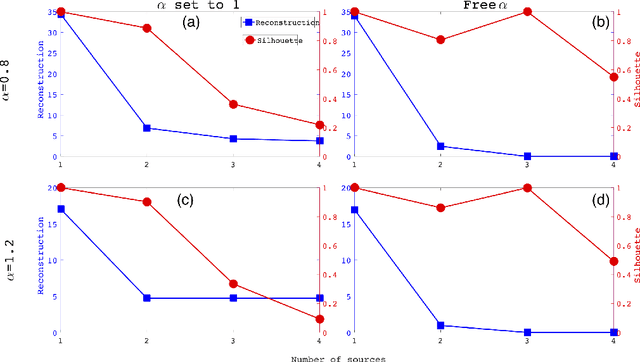
Abstract:Fractional Brownian motion (fBm) is a ubiquitous diffusion process in which the memory effects of the stochastic transport result in the mean squared particle displacement following a power law, $\langle {\Delta r}^2 \rangle \sim t^{\alpha}$, where the diffusion exponent $\alpha$ characterizes whether the transport is subdiffusive, ($\alpha<1$), diffusive ($\alpha = 1$), or superdiffusive, ($\alpha >1$). Due to the abundance of fBm processes in nature, significant efforts have been devoted to the identification and characterization of fBm sources in various phenomena. In practice, the identification of the fBm sources often relies on solving a complex and ill-posed inverse problem based on limited observed data. In the general case, the detected signals are formed by an unknown number of release sources, located at different locations and with different strengths, that act simultaneously. This means that the observed data is composed of mixtures of releases from an unknown number of sources, which makes the traditional inverse modeling approaches unreliable. Here, we report an unsupervised learning method, based on Nonnegative Matrix Factorization, that enables the identification of the unknown number of release sources as well the anomalous diffusion characteristics based on limited observed data and the general form of the corresponding fBm Green's function. We show that our method performs accurately for different types of sources and configurations with a predetermined number of sources with specific characteristics and introduced noise.
* published in physical review research
Decadal climate predictions using sequential learning algorithms
Sep 17, 2015
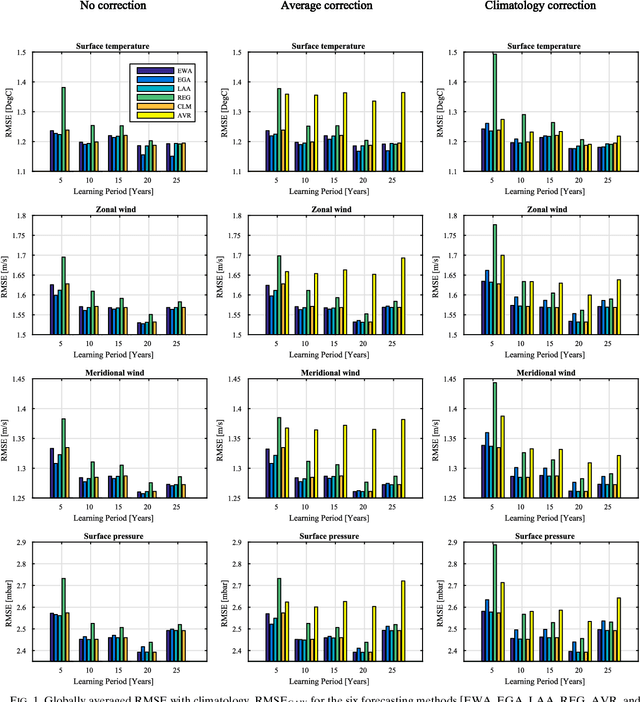

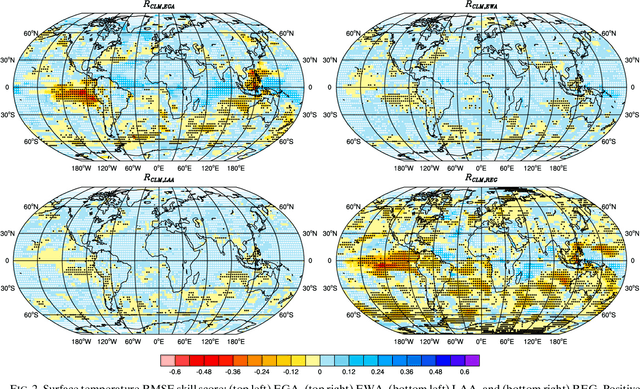
Abstract:Ensembles of climate models are commonly used to improve climate predictions and assess the uncertainties associated with them. Weighting the models according to their performances holds the promise of further improving their predictions. Here, we use an ensemble of decadal climate predictions to demonstrate the ability of sequential learning algorithms (SLAs) to reduce the forecast errors and reduce the uncertainties. Three different SLAs are considered, and their performances are compared with those of an equally weighted ensemble, a linear regression and the climatology. Predictions of four different variables--the surface temperature, the zonal and meridional wind, and pressure--are considered. The spatial distributions of the performances are presented, and the statistical significance of the improvements achieved by the SLAs is tested. Based on the performances of the SLAs, we propose one to be highly suitable for the improvement of decadal climate predictions.
The Contribution of Internal and Model Variabilities to the Uncertainty in CMIP5 Decadal Climate Predictions
Aug 07, 2015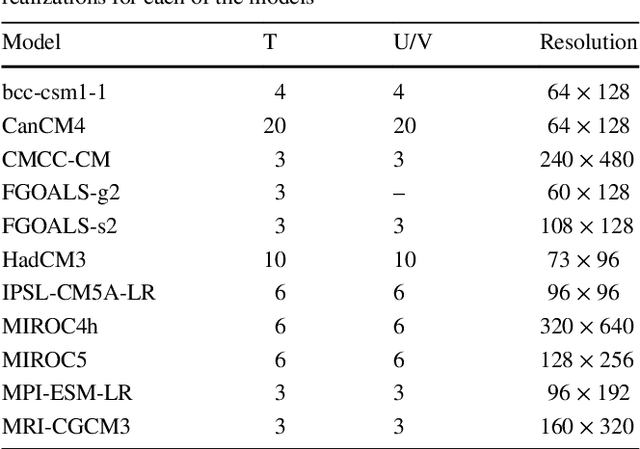
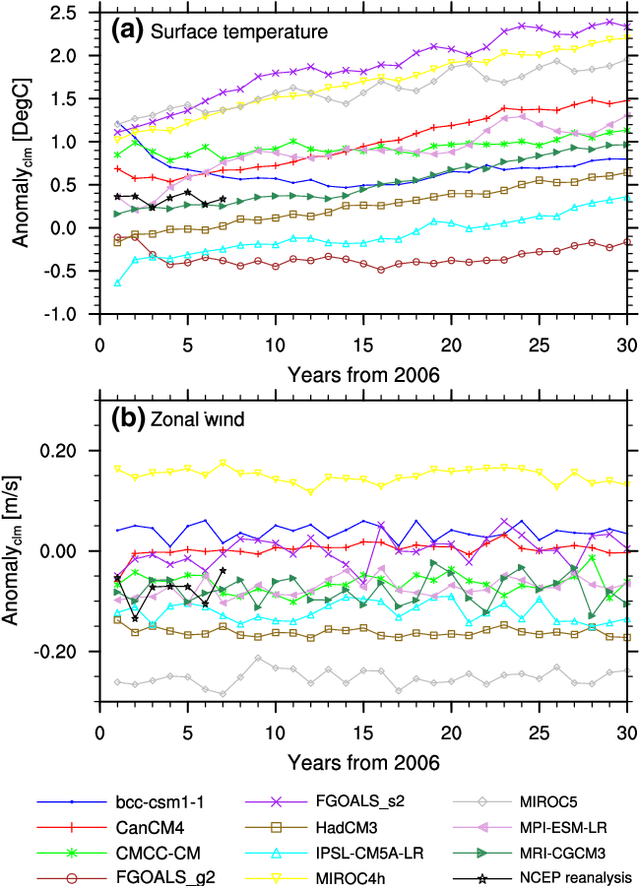
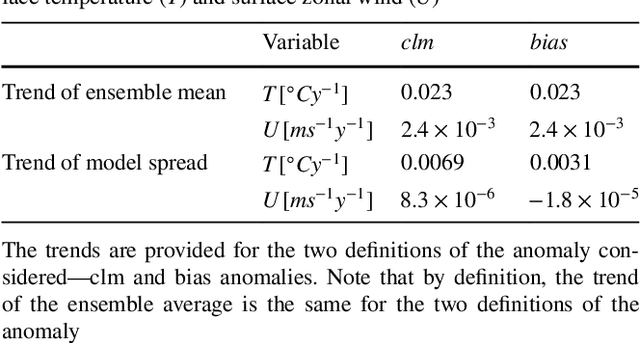
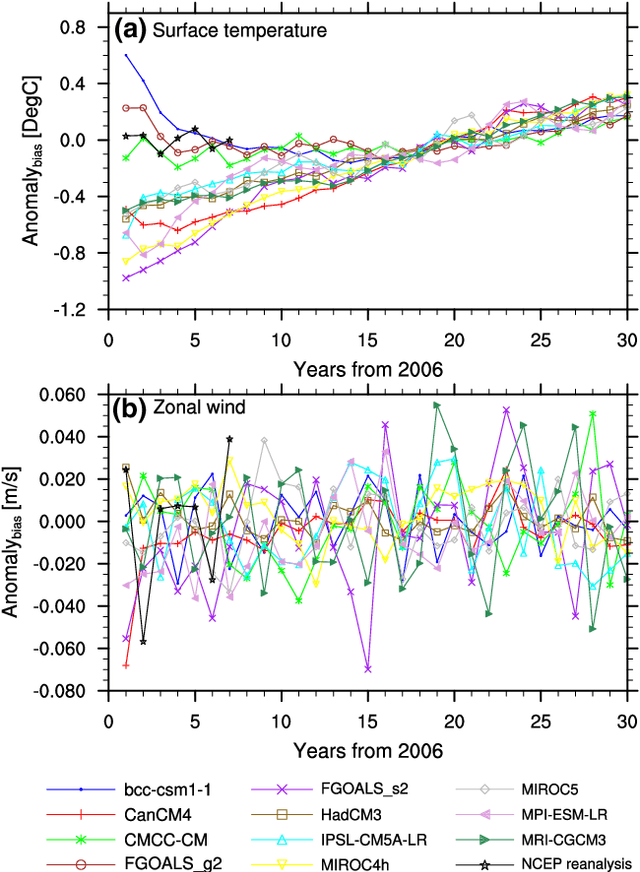
Abstract:Decadal climate predictions, which are initialized with observed conditions, are characterized by two main sources of uncertainties--internal and model variabilities. Using an ensemble of climate model simulations from the CMIP5 decadal experiments, we quantified the total uncertainty associated with these predictions and the relative importance of each source. Annual and monthly averages of the surface temperature and wind components were considered. We show that different definitions of the anomaly results in different conclusions regarding the variance of the ensemble members. However, some features of the uncertainty are common to all the measures we considered. We found that over decadal time scales, there is no considerable increase in the uncertainty with time. The model variability is more sensitive to the annual cycle than the internal variability. This, in turn, results in a maximal uncertainty during the winter in the northern hemisphere. The uncertainty of the surface temperature prediction is dominated by the model variability, whereas the uncertainty of the wind components is determined by both sources. Analysis of the spatial distribution of the uncertainty reveals that the surface temperature has higher variability over land and in high latitudes, whereas the surface zonal wind has higher variability over the ocean. The relative importance of the internal and model variabilities depends on the averaging period, the definition of the anomaly, and the location. These findings suggest that several methods should be combined in order to assess future climate prediction uncertainties and that weighting schemes of the ensemble members may reduce the uncertainties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge