Matrix Factorization for Inferring Associations and Missing Links

Missing link prediction is a method for network analysis, with applications in recommender systems, biology, social sciences, cybersecurity, information retrieval, and Artificial Intelligence (AI) reasoning in Knowledge Graphs. Missing link prediction identifies unseen but potentially existing connections in a network by analyzing the observed patterns and relationships. In proliferation detection, this supports efforts to identify and characterize attempts by state and non-state actors to acquire nuclear weapons or associated technology - a notoriously challenging but vital mission for global security. Dimensionality reduction techniques like Non-Negative Matrix Factorization (NMF) and Logistic Matrix Factorization (LMF) are effective but require selection of the matrix rank parameter, that is, of the number of hidden features, k, to avoid over/under-fitting. We introduce novel Weighted (WNMFk), Boolean (BNMFk), and Recommender (RNMFk) matrix factorization methods, along with ensemble variants incorporating logistic factorization, for link prediction. Our methods integrate automatic model determination for rank estimation by evaluating stability and accuracy using a modified bootstrap methodology and uncertainty quantification (UQ), assessing prediction reliability under random perturbations. We incorporate Otsu threshold selection and k-means clustering for Boolean matrix factorization, comparing them to coordinate descent-based Boolean thresholding. Our experiments highlight the impact of rank k selection, evaluate model performance under varying test-set sizes, and demonstrate the benefits of UQ for reliable predictions using abstention. We validate our methods on three synthetic datasets (Boolean and uniformly distributed) and benchmark them against LMF and symmetric LMF (symLMF) on five real-world protein-protein interaction networks, showcasing an improved prediction performance.

Boolean Matrix Factorization via Nonnegative Auxiliary Optimization

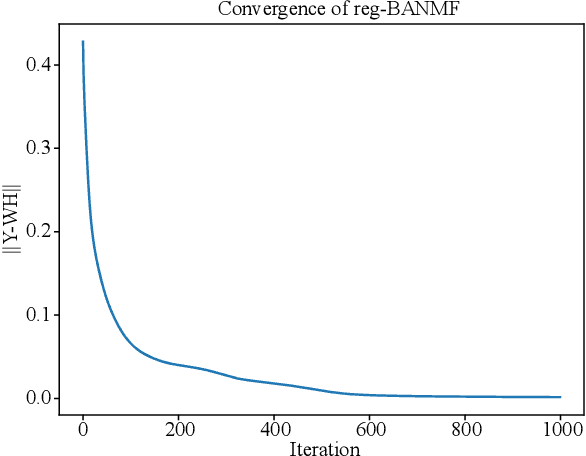
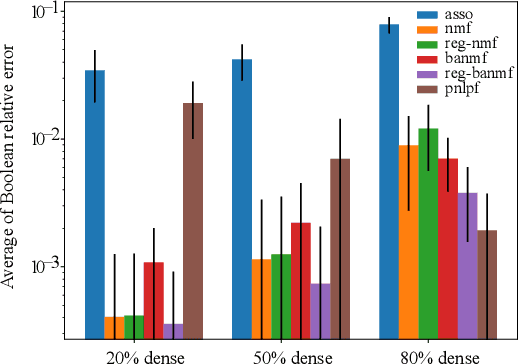
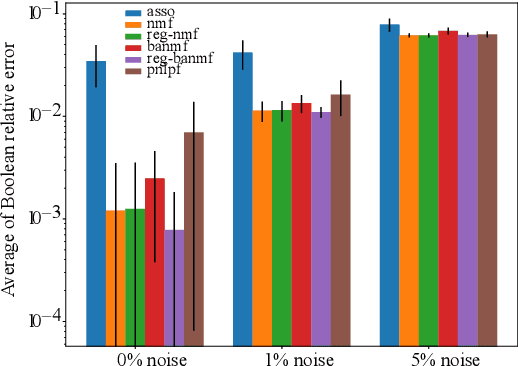
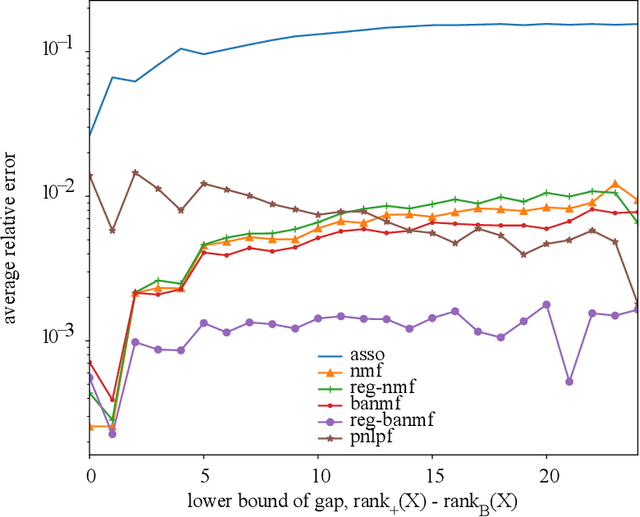
A novel approach to Boolean matrix factorization (BMF) is presented. Instead of solving the BMF problem directly, this approach solves a nonnegative optimization problem with the constraint over an auxiliary matrix whose Boolean structure is identical to the initial Boolean data. Then the solution of the nonnegative auxiliary optimization problem is thresholded to provide a solution for the BMF problem. We provide the proofs for the equivalencies of the two solution spaces under the existence of an exact solution. Moreover, the nonincreasing property of the algorithm is also proven. Experiments on synthetic and real datasets are conducted to show the effectiveness and complexity of the algorithm compared to other current methods.

Determination of Latent Dimensionality in International Trade Flow

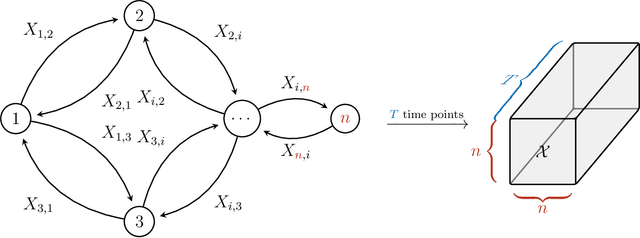
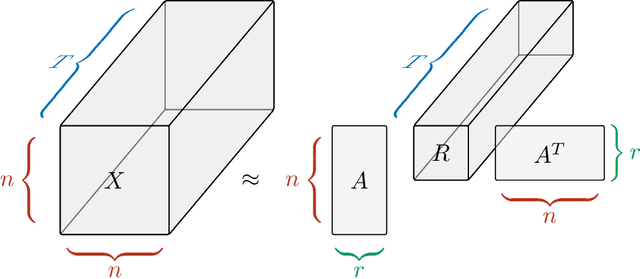
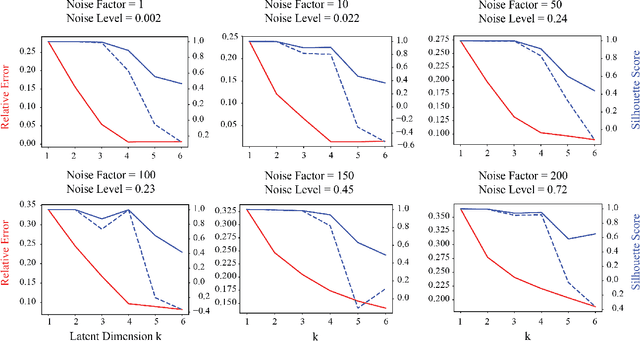
Currently, high-dimensional data is ubiquitous in data science, which necessitates the development of techniques to decompose and interpret such multidimensional (aka tensor) datasets. Finding a low dimensional representation of the data, that is, its inherent structure, is one of the approaches that can serve to understand the dynamics of low dimensional latent features hidden in the data. Nonnegative RESCAL is one such technique, particularly well suited to analyze self-relational data, such as dynamic networks found in international trade flows. Nonnegative RESCAL computes a low dimensional tensor representation by finding the latent space containing multiple modalities. Estimating the dimensionality of this latent space is crucial for extracting meaningful latent features. Here, to determine the dimensionality of the latent space with nonnegative RESCAL, we propose a latent dimension determination method which is based on clustering of the solutions of multiple realizations of nonnegative RESCAL decompositions. We demonstrate the performance of our model selection method on synthetic data and then we apply our method to decompose a network of international trade flows data from International Monetary Fund and validate the resulting features against empirical facts from economic literature.