FedEFM: Federated Endovascular Foundation Model with Unseen Data

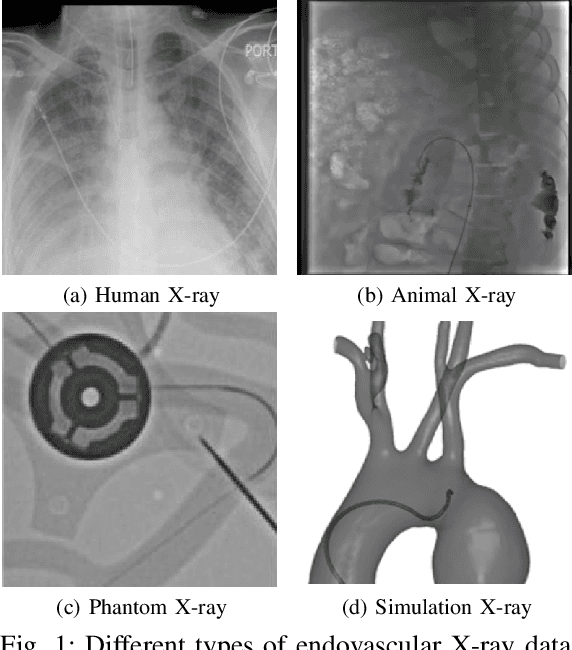
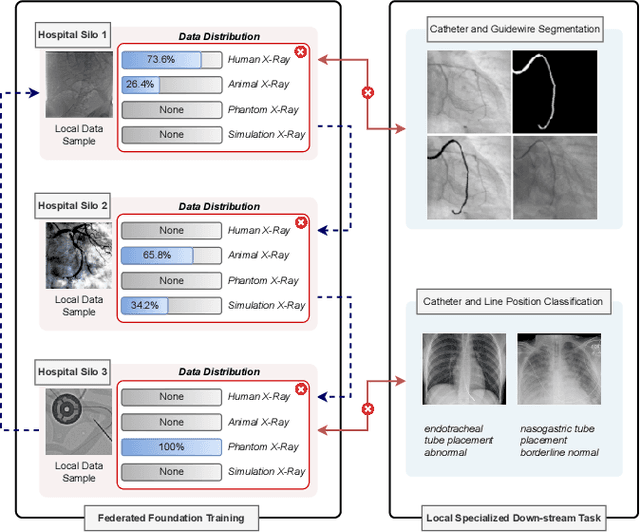
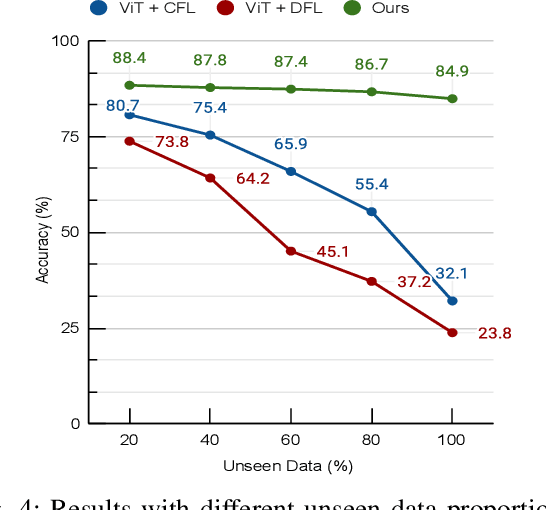
In endovascular surgery, the precise identification of catheters and guidewires in X-ray images is essential for reducing intervention risks. However, accurately segmenting catheter and guidewire structures is challenging due to the limited availability of labeled data. Foundation models offer a promising solution by enabling the collection of similar domain data to train models whose weights can be fine-tuned for downstream tasks. Nonetheless, large-scale data collection for training is constrained by the necessity of maintaining patient privacy. This paper proposes a new method to train a foundation model in a decentralized federated learning setting for endovascular intervention. To ensure the feasibility of the training, we tackle the unseen data issue using differentiable Earth Mover's Distance within a knowledge distillation framework. Once trained, our foundation model's weights provide valuable initialization for downstream tasks, thereby enhancing task-specific performance. Intensive experiments show that our approach achieves new state-of-the-art results, contributing to advancements in endovascular intervention and robotic-assisted endovascular surgery, while addressing the critical issue of data sharing in the medical domain.

Generalization of GANs under Lipschitz continuity and data augmentation

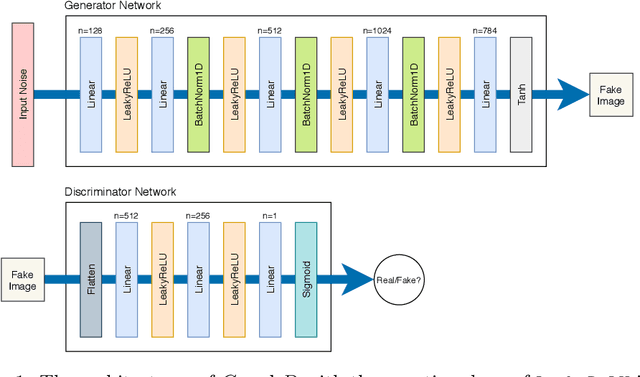
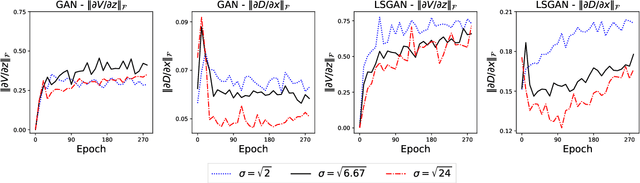
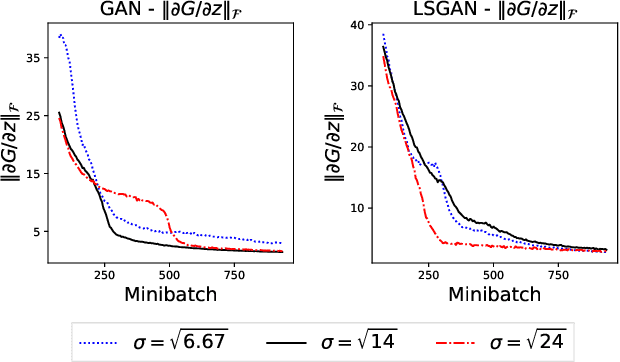
Generative adversarial networks (GANs) have been being widely used in various applications. Arguably, GANs are really complex, and little has been known about their generalization. In this paper, we make a comprehensive analysis about generalization of GANs. We decompose the generalization error into an explicit composition: generator error + discriminator error + optimization error. The first two errors show the capacity of the player's families, are irreducible and optimizer-independent. We then provide both uniform and non-uniform generalization bounds in different scenarios, thanks to our new bridge between Lipschitz continuity and generalization. Our bounds overcome some major limitations of existing ones. In particular, our bounds show that penalizing the zero- and first-order informations of the GAN loss will improve generalization, answering the long mystery of why imposing a Lipschitz constraint can help GANs perform better in practice. Finally, we show why data augmentation penalizes the zero- and first-order informations of the loss, helping the players generalize better, and hence explaining the highly successful use of data augmentation for GANs.