Efficient LLM Inference using Dynamic Input Pruning and Cache-Aware Masking

While mobile devices provide ever more compute power, improvements in DRAM bandwidth are much slower. This is unfortunate for large language model (LLM) token generation, which is heavily memory-bound. Previous work has proposed to leverage natural dynamic activation sparsity in ReLU-activated LLMs to reduce effective DRAM bandwidth per token. However, more recent LLMs use SwiGLU instead of ReLU, which result in little inherent sparsity. While SwiGLU activations can be pruned based on magnitude, the resulting sparsity patterns are difficult to predict, rendering previous approaches ineffective. To circumvent this issue, our work introduces Dynamic Input Pruning (DIP): a predictor-free dynamic sparsification approach, which preserves accuracy with minimal fine-tuning. DIP can further use lightweight LoRA adapters to regain some performance lost during sparsification. Lastly, we describe a novel cache-aware masking strategy, which considers the cache state and activation magnitude to further increase cache hit rate, improving LLM token rate on mobile devices. DIP outperforms other methods in terms of accuracy, memory and throughput trade-offs across simulated hardware settings. On Phi-3-Medium, DIP achieves a 46% reduction in memory and 40% increase in throughput with $<$ 0.1 loss in perplexity.

Mixture of Cache-Conditional Experts for Efficient Mobile Device Inference

Mixture of Experts (MoE) LLMs have recently gained attention for their ability to enhance performance by selectively engaging specialized subnetworks or "experts" for each input. However, deploying MoEs on memory-constrained devices remains challenging, particularly when generating tokens sequentially with a batch size of one, as opposed to typical high-throughput settings involving long sequences or large batches. In this work, we optimize MoE on memory-constrained devices where only a subset of expert weights fit in DRAM. We introduce a novel cache-aware routing strategy that leverages expert reuse during token generation to improve cache locality. We evaluate our approach on language modeling, MMLU, and GSM8K benchmarks and present on-device results demonstrating 2$\times$ speedups on mobile devices, offering a flexible, training-free solution to extend MoE's applicability across real-world applications.

GPTVQ: The Blessing of Dimensionality for LLM Quantization

In this work we show that the size versus accuracy trade-off of neural network quantization can be significantly improved by increasing the quantization dimensionality. We propose the GPTVQ method, a new fast method for post-training vector quantization (VQ) that scales well to Large Language Models (LLMs). Our method interleaves quantization of one or more columns with updates to the remaining unquantized weights, using information from the Hessian of the per-layer output reconstruction MSE. Quantization codebooks are initialized using an efficient data-aware version of the EM algorithm. The codebooks are then updated, and further compressed by using integer quantization and SVD-based compression. GPTVQ establishes a new state-of-the art in the size vs accuracy trade-offs on a wide range of LLMs such as Llama-v2 and Mistral. Furthermore, our method is efficient: on a single H100 it takes between 3 and 11 hours to process a Llamav2-70B model, depending on quantization setting. Lastly, with on-device timings for VQ decompression on a mobile CPU we show that VQ leads to improved latency compared to using a 4-bit integer format.

The LLM Surgeon

State-of-the-art language models are becoming increasingly large in an effort to achieve the highest performance on large corpora of available textual data. However, the sheer size of the Transformer architectures makes it difficult to deploy models within computational, environmental or device-specific constraints. We explore data-driven compression of existing pretrained models as an alternative to training smaller models from scratch. To do so, we scale Kronecker-factored curvature approximations of the target loss landscape to large language models. In doing so, we can compute both the dynamic allocation of structures that can be removed as well as updates of remaining weights that account for the removal. We provide a general framework for unstructured, semi-structured and structured pruning and improve upon weight updates to capture more correlations between weights, while remaining computationally efficient. Experimentally, our method can prune rows and columns from a range of OPT models and Llamav2-7B by 20%-30%, with a negligible loss in performance, and achieve state-of-the-art results in unstructured and semi-structured pruning of large language models.

QBitOpt: Fast and Accurate Bitwidth Reallocation during Training

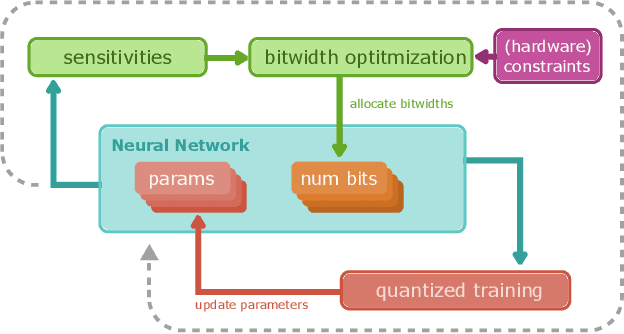
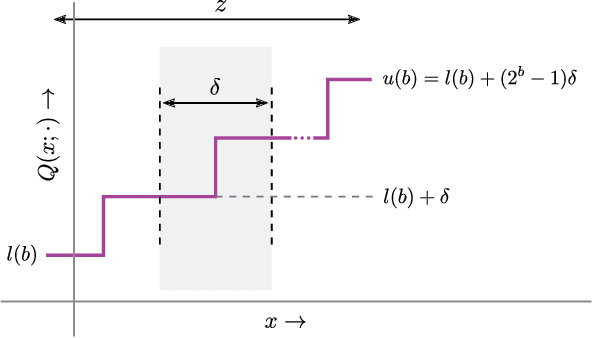
Quantizing neural networks is one of the most effective methods for achieving efficient inference on mobile and embedded devices. In particular, mixed precision quantized (MPQ) networks, whose layers can be quantized to different bitwidths, achieve better task performance for the same resource constraint compared to networks with homogeneous bitwidths. However, finding the optimal bitwidth allocation is a challenging problem as the search space grows exponentially with the number of layers in the network. In this paper, we propose QBitOpt, a novel algorithm for updating bitwidths during quantization-aware training (QAT). We formulate the bitwidth allocation problem as a constraint optimization problem. By combining fast-to-compute sensitivities with efficient solvers during QAT, QBitOpt can produce mixed-precision networks with high task performance guaranteed to satisfy strict resource constraints. This contrasts with existing mixed-precision methods that learn bitwidths using gradients and cannot provide such guarantees. We evaluate QBitOpt on ImageNet and confirm that we outperform existing fixed and mixed-precision methods under average bitwidth constraints commonly found in the literature.

Pruning vs Quantization: Which is Better?

Neural network pruning and quantization techniques are almost as old as neural networks themselves. However, to date only ad-hoc comparisons between the two have been published. In this paper, we set out to answer the question on which is better: neural network quantization or pruning? By answering this question, we hope to inform design decisions made on neural network hardware going forward. We provide an extensive comparison between the two techniques for compressing deep neural networks. First, we give an analytical comparison of expected quantization and pruning error for general data distributions. Then, we provide lower bounds for the per-layer pruning and quantization error in trained networks, and compare these to empirical error after optimization. Finally, we provide an extensive experimental comparison for training 8 large-scale models on 3 tasks. Our results show that in most cases quantization outperforms pruning. Only in some scenarios with very high compression ratio, pruning might be beneficial from an accuracy standpoint.

FP8 versus INT8 for efficient deep learning inference

Recently, the idea of using FP8 as a number format for neural network training has been floating around the deep learning world. Given that most training is currently conducted with entire networks in FP32, or sometimes FP16 with mixed-precision, the step to having some parts of a network run in FP8 with 8-bit weights is an appealing potential speed-up for the generally costly and time-intensive training procedures in deep learning. A natural question arises regarding what this development means for efficient inference on edge devices. In the efficient inference device world, workloads are frequently executed in INT8. Sometimes going even as low as INT4 when efficiency calls for it. In this whitepaper, we compare the performance for both the FP8 and INT formats for efficient on-device inference. We theoretically show the difference between the INT and FP formats for neural networks and present a plethora of post-training quantization and quantization-aware-training results to show how this theory translates to practice. We also provide a hardware analysis showing that the FP formats are somewhere between 50-180% less efficient in terms of compute in dedicated hardware than the INT format. Based on our research and a read of the research field, we conclude that although the proposed FP8 format could be good for training, the results for inference do not warrant a dedicated implementation of FP8 in favor of INT8 for efficient inference. We show that our results are mostly consistent with previous findings but that important comparisons between the formats have thus far been lacking. Finally, we discuss what happens when FP8-trained networks are converted to INT8 and conclude with a brief discussion on the most efficient way for on-device deployment and an extensive suite of INT8 results for many models.

A Practical Mixed Precision Algorithm for Post-Training Quantization

Neural network quantization is frequently used to optimize model size, latency and power consumption for on-device deployment of neural networks. In many cases, a target bit-width is set for an entire network, meaning every layer get quantized to the same number of bits. However, for many networks some layers are significantly more robust to quantization noise than others, leaving an important axis of improvement unused. As many hardware solutions provide multiple different bit-width settings, mixed-precision quantization has emerged as a promising solution to find a better performance-efficiency trade-off than homogeneous quantization. However, most existing mixed precision algorithms are rather difficult to use for practitioners as they require access to the training data, have many hyper-parameters to tune or even depend on end-to-end retraining of the entire model. In this work, we present a simple post-training mixed precision algorithm that only requires a small unlabeled calibration dataset to automatically select suitable bit-widths for each layer for desirable on-device performance. Our algorithm requires no hyper-parameter tuning, is robust to data variation and takes into account practical hardware deployment constraints making it a great candidate for practical use. We experimentally validate our proposed method on several computer vision tasks, natural language processing tasks and many different networks, and show that we can find mixed precision networks that provide a better trade-off between accuracy and efficiency than their homogeneous bit-width equivalents.

Quantized Sparse Weight Decomposition for Neural Network Compression

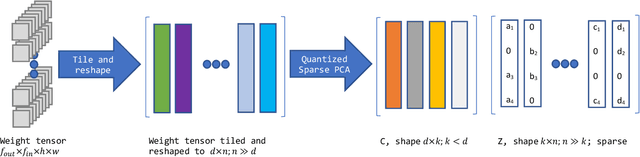
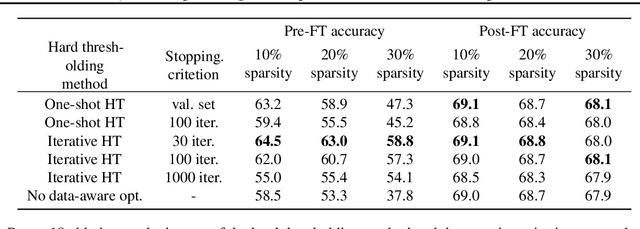
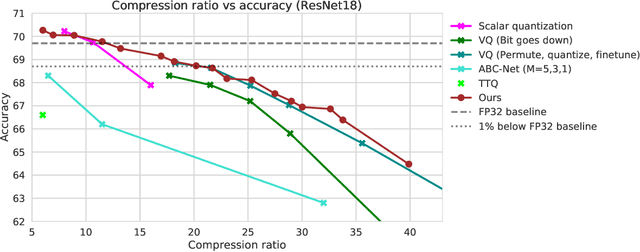
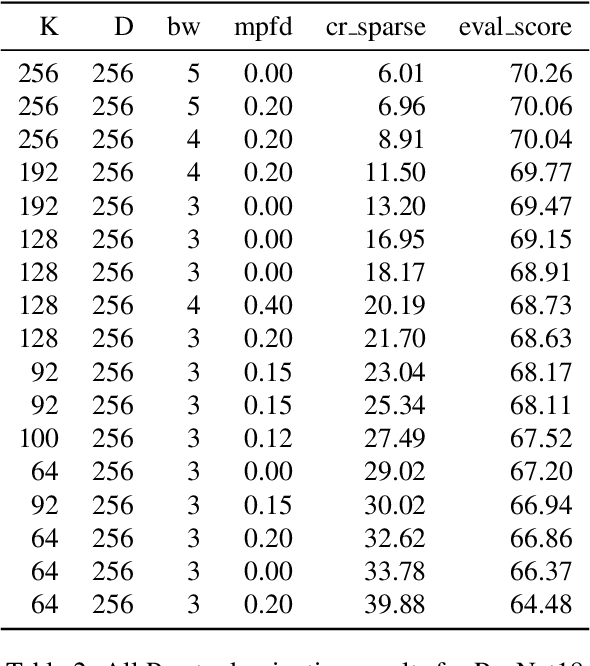
In this paper, we introduce a novel method of neural network weight compression. In our method, we store weight tensors as sparse, quantized matrix factors, whose product is computed on the fly during inference to generate the target model's weights. We use projected gradient descent methods to find quantized and sparse factorization of the weight tensors. We show that this approach can be seen as a unification of weight SVD, vector quantization, and sparse PCA. Combined with end-to-end fine-tuning our method exceeds or is on par with previous state-of-the-art methods in terms of the trade-off between accuracy and model size. Our method is applicable to both moderate compression regimes, unlike vector quantization, and extreme compression regimes.

Cyclical Pruning for Sparse Neural Networks

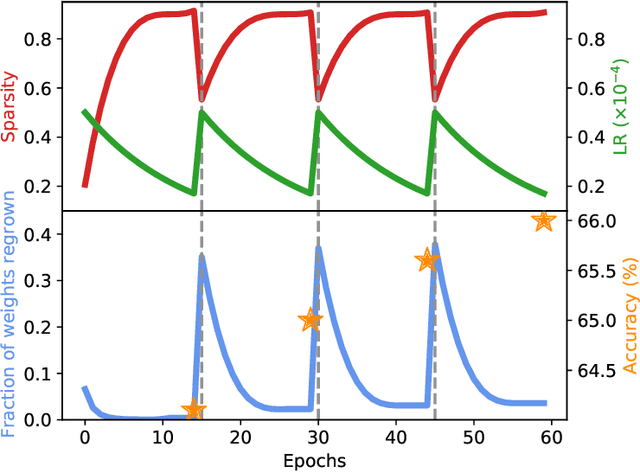
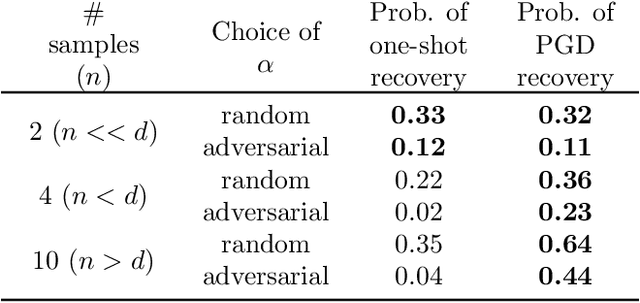
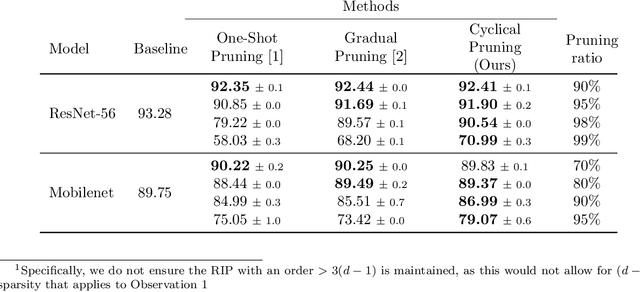
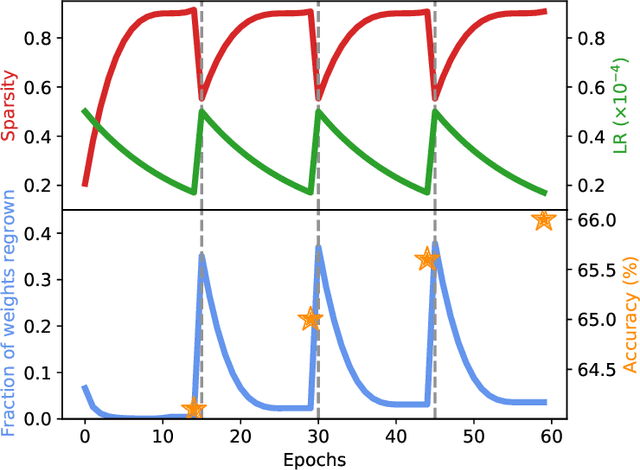
Current methods for pruning neural network weights iteratively apply magnitude-based pruning on the model weights and re-train the resulting model to recover lost accuracy. In this work, we show that such strategies do not allow for the recovery of erroneously pruned weights. To enable weight recovery, we propose a simple strategy called \textit{cyclical pruning} which requires the pruning schedule to be periodic and allows for weights pruned erroneously in one cycle to recover in subsequent ones. Experimental results on both linear models and large-scale deep neural networks show that cyclical pruning outperforms existing pruning algorithms, especially at high sparsity ratios. Our approach is easy to tune and can be readily incorporated into existing pruning pipelines to boost performance.