GPTVQ: The Blessing of Dimensionality for LLM Quantization

In this work we show that the size versus accuracy trade-off of neural network quantization can be significantly improved by increasing the quantization dimensionality. We propose the GPTVQ method, a new fast method for post-training vector quantization (VQ) that scales well to Large Language Models (LLMs). Our method interleaves quantization of one or more columns with updates to the remaining unquantized weights, using information from the Hessian of the per-layer output reconstruction MSE. Quantization codebooks are initialized using an efficient data-aware version of the EM algorithm. The codebooks are then updated, and further compressed by using integer quantization and SVD-based compression. GPTVQ establishes a new state-of-the art in the size vs accuracy trade-offs on a wide range of LLMs such as Llama-v2 and Mistral. Furthermore, our method is efficient: on a single H100 it takes between 3 and 11 hours to process a Llamav2-70B model, depending on quantization setting. Lastly, with on-device timings for VQ decompression on a mobile CPU we show that VQ leads to improved latency compared to using a 4-bit integer format.

Pruning vs Quantization: Which is Better?

Neural network pruning and quantization techniques are almost as old as neural networks themselves. However, to date only ad-hoc comparisons between the two have been published. In this paper, we set out to answer the question on which is better: neural network quantization or pruning? By answering this question, we hope to inform design decisions made on neural network hardware going forward. We provide an extensive comparison between the two techniques for compressing deep neural networks. First, we give an analytical comparison of expected quantization and pruning error for general data distributions. Then, we provide lower bounds for the per-layer pruning and quantization error in trained networks, and compare these to empirical error after optimization. Finally, we provide an extensive experimental comparison for training 8 large-scale models on 3 tasks. Our results show that in most cases quantization outperforms pruning. Only in some scenarios with very high compression ratio, pruning might be beneficial from an accuracy standpoint.

FP8 versus INT8 for efficient deep learning inference

Recently, the idea of using FP8 as a number format for neural network training has been floating around the deep learning world. Given that most training is currently conducted with entire networks in FP32, or sometimes FP16 with mixed-precision, the step to having some parts of a network run in FP8 with 8-bit weights is an appealing potential speed-up for the generally costly and time-intensive training procedures in deep learning. A natural question arises regarding what this development means for efficient inference on edge devices. In the efficient inference device world, workloads are frequently executed in INT8. Sometimes going even as low as INT4 when efficiency calls for it. In this whitepaper, we compare the performance for both the FP8 and INT formats for efficient on-device inference. We theoretically show the difference between the INT and FP formats for neural networks and present a plethora of post-training quantization and quantization-aware-training results to show how this theory translates to practice. We also provide a hardware analysis showing that the FP formats are somewhere between 50-180% less efficient in terms of compute in dedicated hardware than the INT format. Based on our research and a read of the research field, we conclude that although the proposed FP8 format could be good for training, the results for inference do not warrant a dedicated implementation of FP8 in favor of INT8 for efficient inference. We show that our results are mostly consistent with previous findings but that important comparisons between the formats have thus far been lacking. Finally, we discuss what happens when FP8-trained networks are converted to INT8 and conclude with a brief discussion on the most efficient way for on-device deployment and an extensive suite of INT8 results for many models.

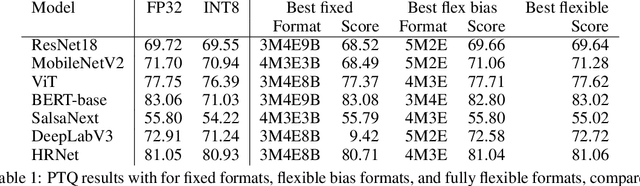
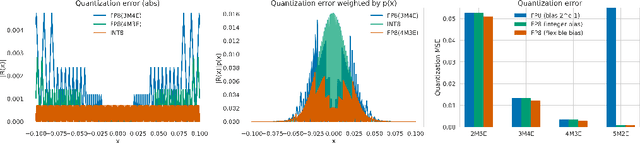
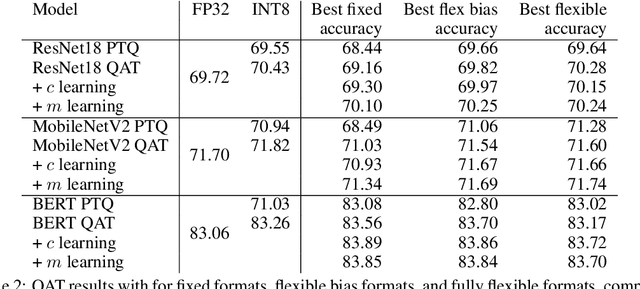
FP8 Quantization: The Power of the Exponent

When quantizing neural networks for efficient inference, low-bit integers are the go-to format for efficiency. However, low-bit floating point numbers have an extra degree of freedom, assigning some bits to work on an exponential scale instead. This paper in-depth investigates this benefit of the floating point format for neural network inference. We detail the choices that can be made for the FP8 format, including the important choice of the number of bits for the mantissa and exponent, and show analytically in which settings these choices give better performance. Then we show how these findings translate to real networks, provide an efficient implementation for FP8 simulation, and a new algorithm that enables the learning of both the scale parameters and the number of exponent bits in the FP8 format. Our chief conclusion is that when doing post-training quantization for a wide range of networks, the FP8 format is better than INT8 in terms of accuracy, and the choice of the number of exponent bits is driven by the severity of outliers in the network. We also conduct experiments with quantization-aware training where the difference in formats disappears as the network is trained to reduce the effect of outliers.

Quantized Sparse Weight Decomposition for Neural Network Compression

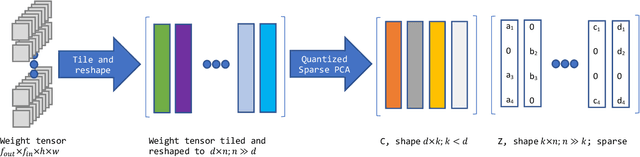
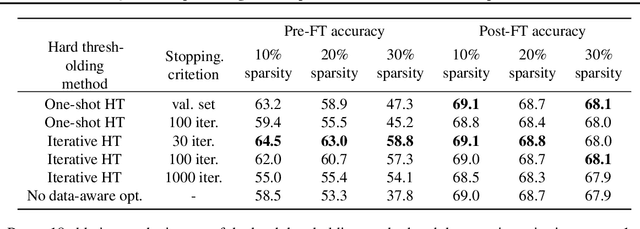
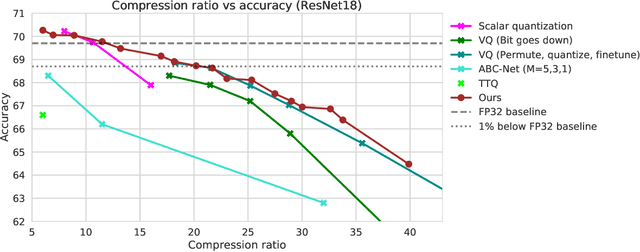
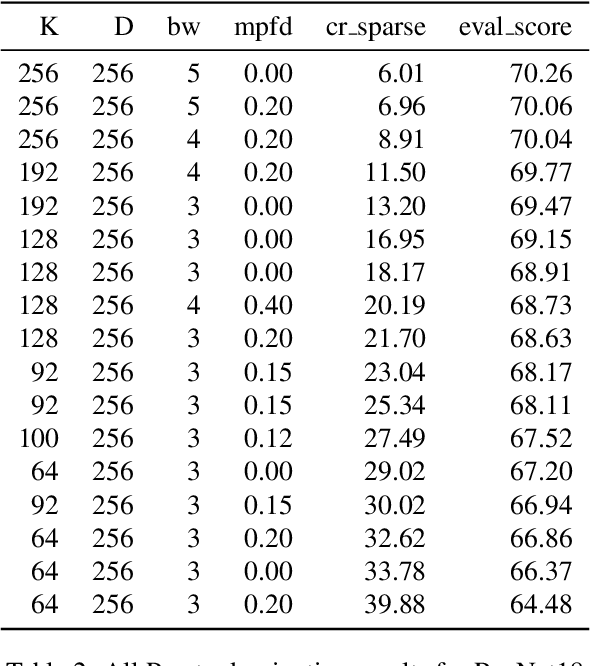
In this paper, we introduce a novel method of neural network weight compression. In our method, we store weight tensors as sparse, quantized matrix factors, whose product is computed on the fly during inference to generate the target model's weights. We use projected gradient descent methods to find quantized and sparse factorization of the weight tensors. We show that this approach can be seen as a unification of weight SVD, vector quantization, and sparse PCA. Combined with end-to-end fine-tuning our method exceeds or is on par with previous state-of-the-art methods in terms of the trade-off between accuracy and model size. Our method is applicable to both moderate compression regimes, unlike vector quantization, and extreme compression regimes.

Cyclical Pruning for Sparse Neural Networks

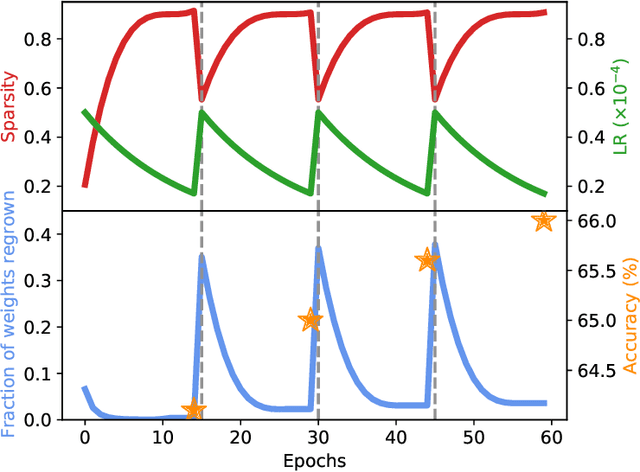
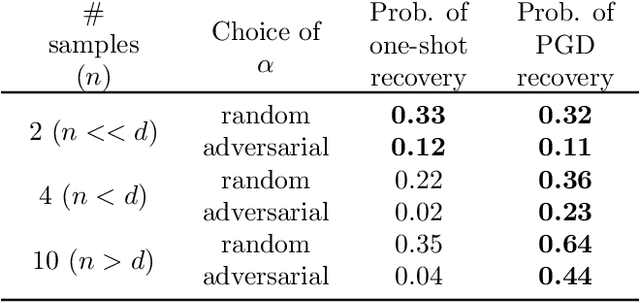
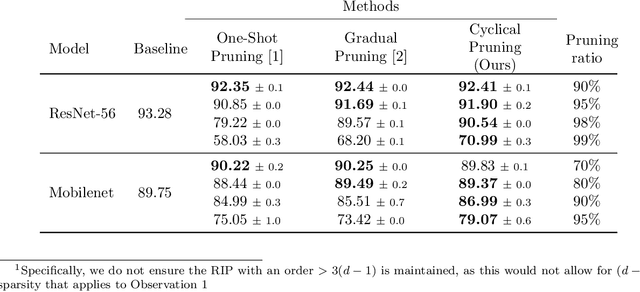
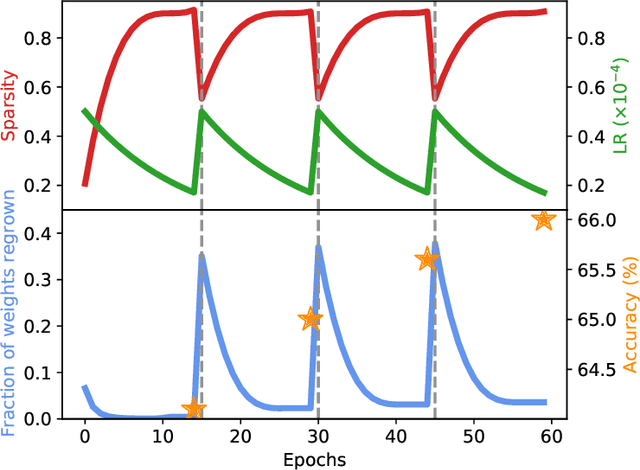
Current methods for pruning neural network weights iteratively apply magnitude-based pruning on the model weights and re-train the resulting model to recover lost accuracy. In this work, we show that such strategies do not allow for the recovery of erroneously pruned weights. To enable weight recovery, we propose a simple strategy called \textit{cyclical pruning} which requires the pruning schedule to be periodic and allows for weights pruned erroneously in one cycle to recover in subsequent ones. Experimental results on both linear models and large-scale deep neural networks show that cyclical pruning outperforms existing pruning algorithms, especially at high sparsity ratios. Our approach is easy to tune and can be readily incorporated into existing pruning pipelines to boost performance.

Taxonomy and Evaluation of Structured Compression of Convolutional Neural Networks

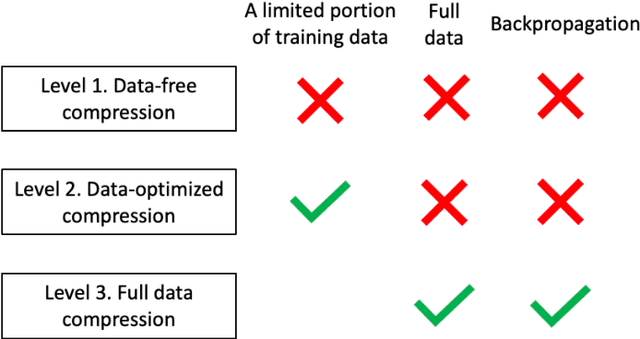
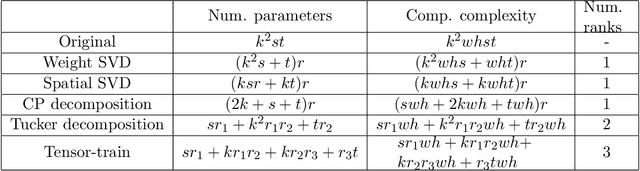
The success of deep neural networks in many real-world applications is leading to new challenges in building more efficient architectures. One effective way of making networks more efficient is neural network compression. We provide an overview of existing neural network compression methods that can be used to make neural networks more efficient by changing the architecture of the network. First, we introduce a new way to categorize all published compression methods, based on the amount of data and compute needed to make the methods work in practice. These are three 'levels of compression solutions'. Second, we provide a taxonomy of tensor factorization based and probabilistic compression methods. Finally, we perform an extensive evaluation of different compression techniques from the literature for models trained on ImageNet. We show that SVD and probabilistic compression or pruning methods are complementary and give the best results of all the considered methods. We also provide practical ways to combine them.

End-to-end Learning of Cost-Volume Aggregation for Real-time Dense Stereo

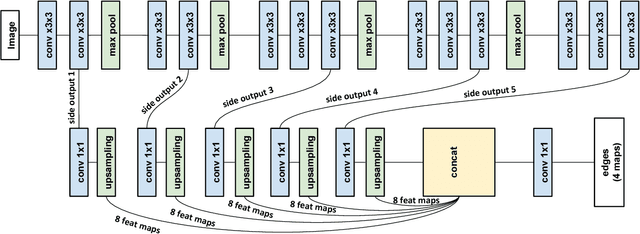
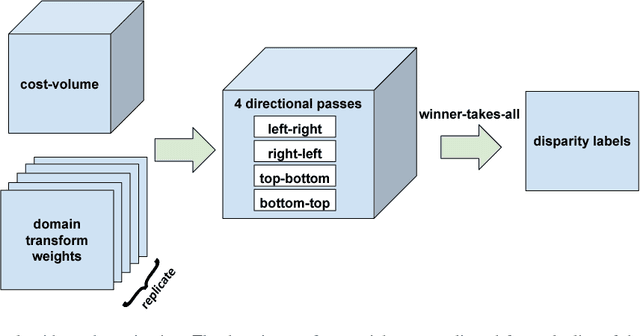
We present a new deep learning-based approach for dense stereo matching. Compared to previous works, our approach does not use deep learning of pixel appearance descriptors, employing very fast classical matching scores instead. At the same time, our approach uses a deep convolutional network to predict the local parameters of cost volume aggregation process, which in this paper we implement using differentiable domain transform. By treating such transform as a recurrent neural network, we are able to train our whole system that includes cost volume computation, cost-volume aggregation (smoothing), and winner-takes-all disparity selection end-to-end. The resulting method is highly efficient at test time, while achieving good matching accuracy. On the KITTI 2015 benchmark, it achieves a result of 6.34\% error rate while running at 29 frames per second rate on a modern GPU.