Lipu Zhou
Camera Pose Refinement via 3D Gaussian Splatting
Aug 25, 2025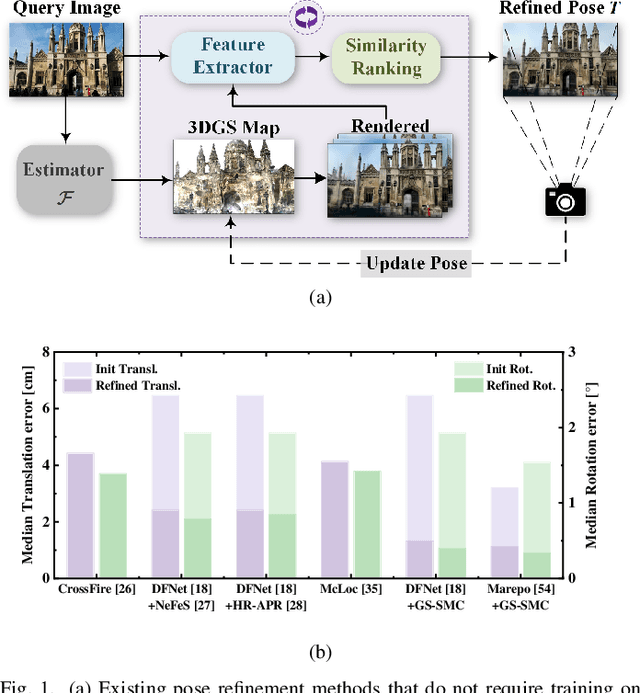
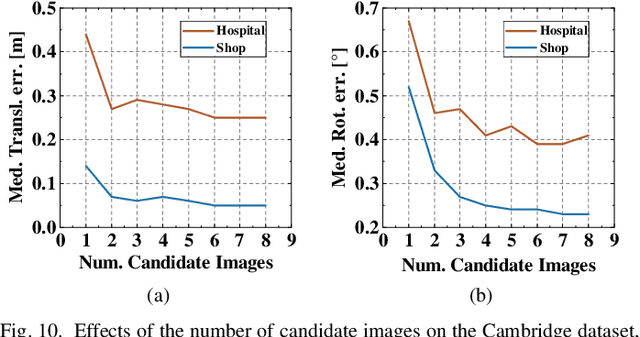

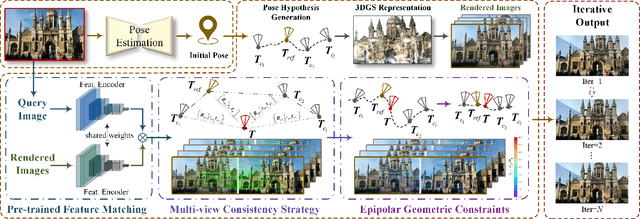
Abstract:Camera pose refinement aims at improving the accuracy of initial pose estimation for applications in 3D computer vision. Most refinement approaches rely on 2D-3D correspondences with specific descriptors or dedicated networks, requiring reconstructing the scene again for a different descriptor or fully retraining the network for each scene. Some recent methods instead infer pose from feature similarity, but their lack of geometry constraints results in less accuracy. To overcome these limitations, we propose a novel camera pose refinement framework leveraging 3D Gaussian Splatting (3DGS), referred to as GS-SMC. Given the widespread usage of 3DGS, our method can employ an existing 3DGS model to render novel views, providing a lightweight solution that can be directly applied to diverse scenes without additional training or fine-tuning. Specifically, we introduce an iterative optimization approach, which refines the camera pose using epipolar geometric constraints among the query and multiple rendered images. Our method allows flexibly choosing feature extractors and matchers to establish these constraints. Extensive empirical evaluations on the 7-Scenes and the Cambridge Landmarks datasets demonstrate that our method outperforms state-of-the-art camera pose refinement approaches, achieving 53.3% and 56.9% reductions in median translation and rotation errors on 7-Scenes, and 40.7% and 53.2% on Cambridge.
Ada3D : Exploiting the Spatial Redundancy with Adaptive Inference for Efficient 3D Object Detection
Jul 17, 2023



Abstract:Voxel-based methods have achieved state-of-the-art performance for 3D object detection in autonomous driving. However, their significant computational and memory costs pose a challenge for their application to resource-constrained vehicles. One reason for this high resource consumption is the presence of a large number of redundant background points in Lidar point clouds, resulting in spatial redundancy in both 3D voxel and dense BEV map representations. To address this issue, we propose an adaptive inference framework called Ada3D, which focuses on exploiting the input-level spatial redundancy. Ada3D adaptively filters the redundant input, guided by a lightweight importance predictor and the unique properties of the Lidar point cloud. Additionally, we utilize the BEV features' intrinsic sparsity by introducing the Sparsity Preserving Batch Normalization. With Ada3D, we achieve 40% reduction for 3D voxels and decrease the density of 2D BEV feature maps from 100% to 20% without sacrificing accuracy. Ada3D reduces the model computational and memory cost by 5x, and achieves 1.52x/1.45x end-to-end GPU latency and 1.5x/4.5x GPU peak memory optimization for the 3D and 2D backbone respectively.
Efficient Second-Order Plane Adjustment
Nov 21, 2022Abstract:Planes are generally used in 3D reconstruction for depth sensors, such as RGB-D cameras and LiDARs. This paper focuses on the problem of estimating the optimal planes and sensor poses to minimize the point-to-plane distance. The resulting least-squares problem is referred to as plane adjustment (PA) in the literature, which is the counterpart of bundle adjustment (BA) in visual reconstruction. Iterative methods are adopted to solve these least-squares problems. Typically, Newton's method is rarely used for a large-scale least-squares problem, due to the high computational complexity of the Hessian matrix. Instead, methods using an approximation of the Hessian matrix, such as the Levenberg-Marquardt (LM) method, are generally adopted. This paper challenges this ingrained idea. We adopt the Newton's method to efficiently solve the PA problem. Specifically, given poses, the optimal planes have close-form solutions. Thus we can eliminate planes from the cost function, which significantly reduces the number of variables. Furthermore, as the optimal planes are functions of poses, this method actually ensures that the optimal planes for the current estimated poses can be obtained at each iteration, which benefits the convergence. The difficulty lies in how to efficiently compute the Hessian matrix and the gradient of the resulting cost. This paper provides an efficient solution. Empirical evaluation shows that our algorithm converges significantly faster than the widely used LM algorithm.
Point Cloud Change Detection With Stereo V-SLAM:Dataset, Metrics and Baseline
Jul 01, 2022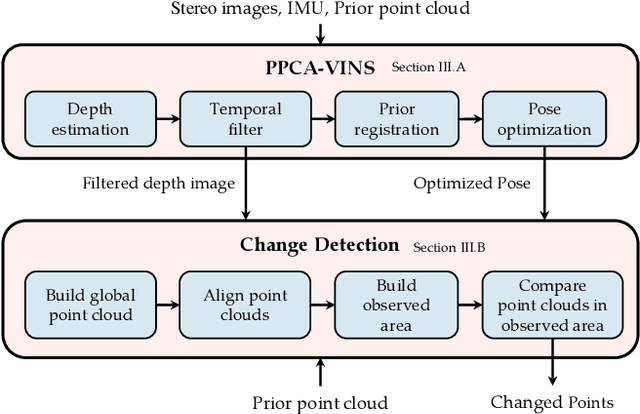
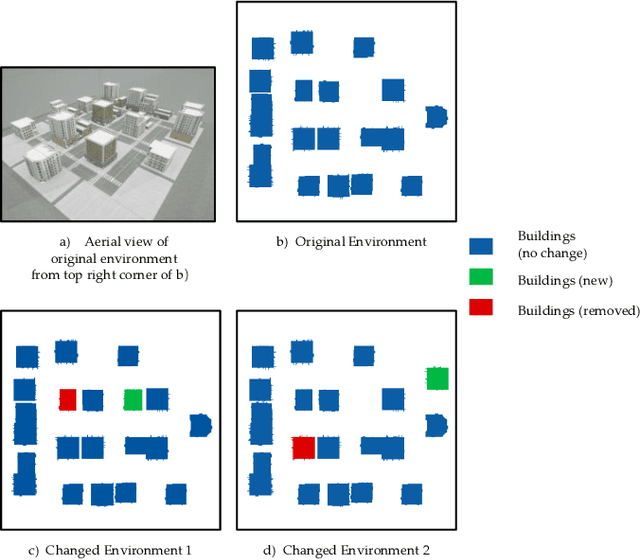
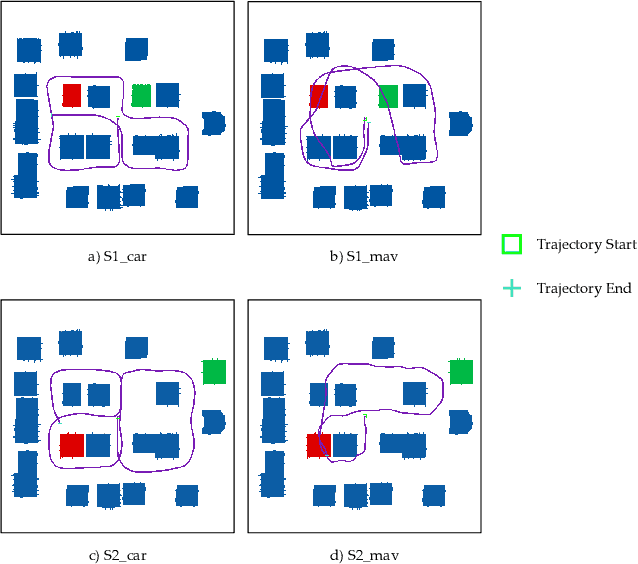
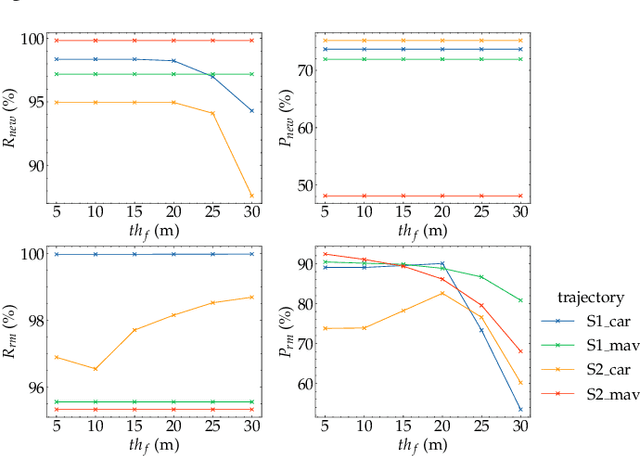
Abstract:Localization and navigation are basic robotic tasks requiring an accurate and up-to-date map to finish these tasks, with crowdsourced data to detect map changes posing an appealing solution. Collecting and processing crowdsourced data requires low-cost sensors and algorithms, but existing methods rely on expensive sensors or computationally expensive algorithms. Additionally, there is no existing dataset to evaluate point cloud change detection. Thus, this paper proposes a novel framework using low-cost sensors like stereo cameras and IMU to detect changes in a point cloud map. Moreover, we create a dataset and the corresponding metrics to evaluate point cloud change detection with the help of the high-fidelity simulator Unreal Engine 4. Experiments show that our visualbased framework can effectively detect the changes in our dataset.
Observation Contribution Theory for Pose Estimation Accuracy
Nov 15, 2021
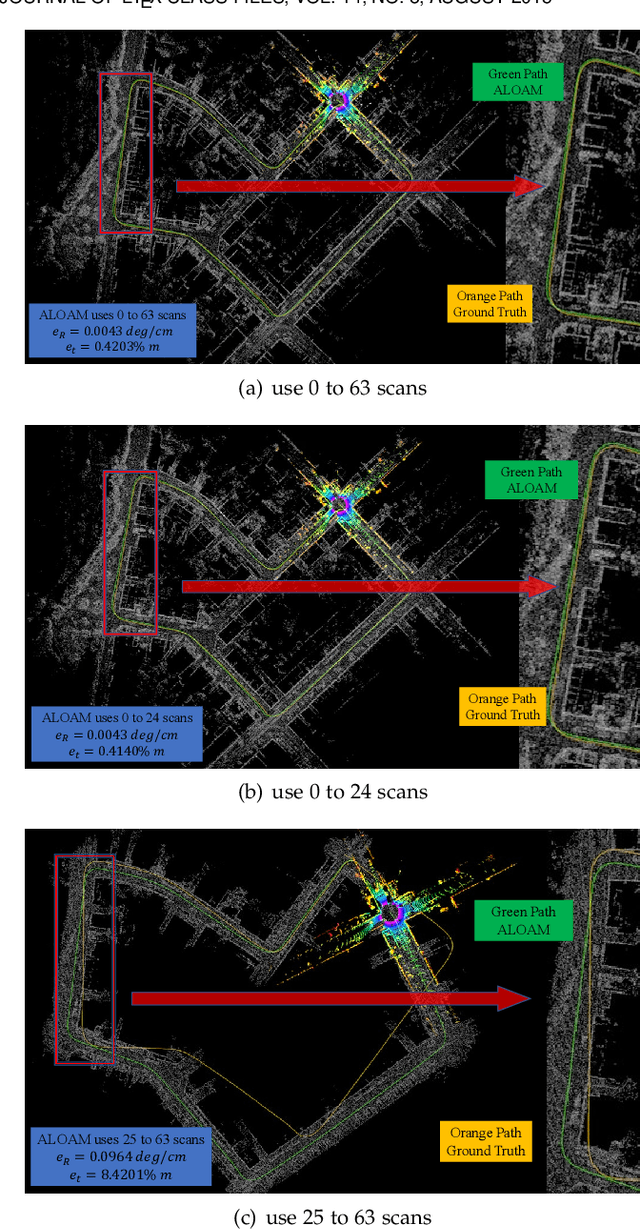

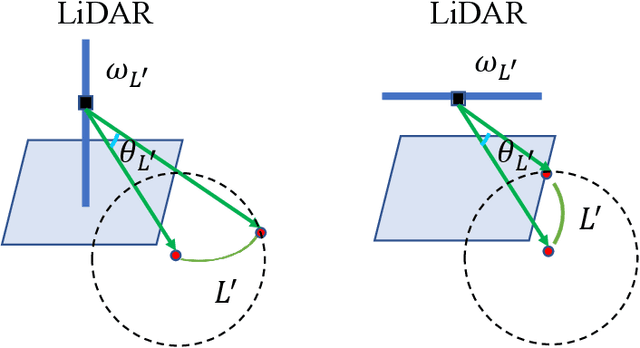
Abstract:The improvement of pose estimation accuracy is currently the fundamental problem in mobile robots. This study aims to improve the use of observations to enhance accuracy. The selection of feature points affects the accuracy of pose estimation, leading to the question of how the contribution of observation influences the system. Accordingly, the contribution of information to the pose estimation process is analyzed. Moreover, the uncertainty model, sensitivity model, and contribution theory are formulated, providing a method for calculating the contribution of every residual term. The proposed selection method has been theoretically proven capable of achieving a global statistical optimum. The proposed method is tested on artificial data simulations and compared with the KITTI benchmark. The experiments revealed superior results in contrast to ALOAM and MLOAM. The proposed algorithm is implemented in LiDAR odometry and LiDAR Inertial odometry both indoors and outdoors using diverse LiDAR sensors with different scan modes, demonstrating its effectiveness in improving pose estimation accuracy. A new configuration of two laser scan sensors is subsequently inferred. The configuration is valid for three-dimensional pose localization in a prior map and yields results at the centimeter level.
An Efficient Planar Bundle Adjustment Algorithm
May 30, 2020
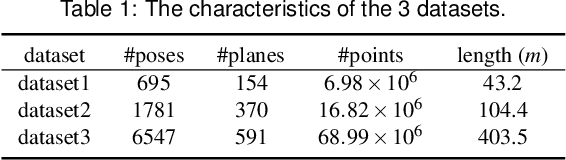
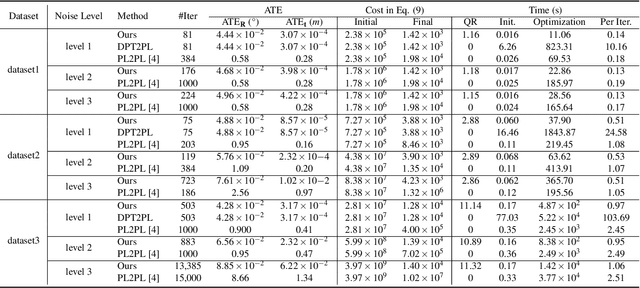
Abstract:This paper presents an efficient algorithm for the least-squares problem using the point-to-plane cost, which aims to jointly optimize depth sensor poses and plane parameters for 3D reconstruction. We call this least-squares problem \textbf{Planar Bundle Adjustment} (PBA), due to the similarity between this problem and the original Bundle Adjustment (BA) in visual reconstruction. As planes ubiquitously exist in the man-made environment, they are generally used as landmarks in SLAM algorithms for various depth sensors. PBA is important to reduce drift and improve the quality of the map. However, directly adopting the well-established BA framework in visual reconstruction will result in a very inefficient solution for PBA. This is because a 3D point only has one observation at a camera pose. In contrast, a depth sensor can record hundreds of points in a plane at a time, which results in a very large nonlinear least-squares problem even for a small-scale space. Fortunately, we find that there exist a special structure of the PBA problem. We introduce a reduced Jacobian matrix and a reduced residual vector, and prove that they can replace the original Jacobian matrix and residual vector in the generally adopted Levenberg-Marquardt (LM) algorithm. This significantly reduces the computational cost. Besides, when planes are combined with other features for 3D reconstruction, the reduced Jacobian matrix and residual vector can also replace the corresponding parts derived from planes. Our experimental results verify that our algorithm can significantly reduce the computational time compared to the solution using the traditional BA framework. Besides, our algorithm is faster, more accuracy, and more robust to initialization errors compared to the start-of-the-art solution using the plane-to-plane cost
Do not Omit Local Minimizer: a Complete Solution for Pose Estimation from 3D Correspondences
Apr 04, 2019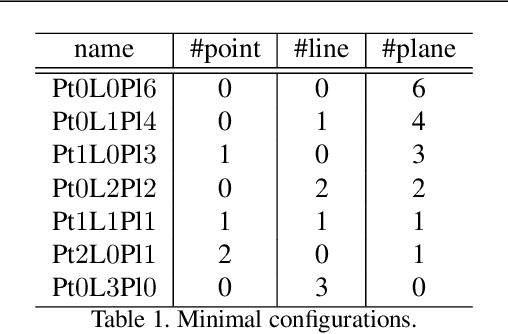
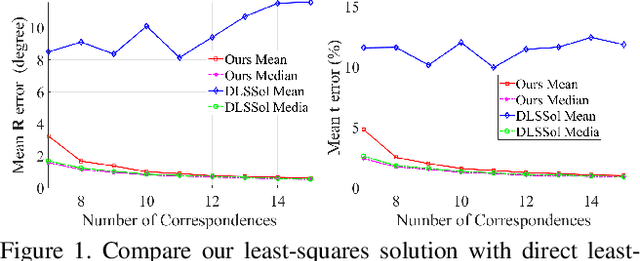

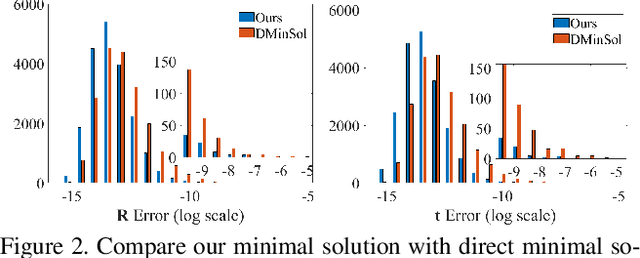
Abstract:Estimating pose from given 3D correspondences, including point-to-point, point-to-line and point-to-plane correspondences, is a fundamental task in computer vision with many applications. We present a complete solution for this task, including a solution for the minimal problem and the least-squares problem of this task. Previous works mainly focused on finding the global minimizer to address the least-squares problem. However, existing works that show the ability to achieve global minimizer are still unsuitable for real-time applications. Furthermore, as one of contributions of this paper, we prove that there exist ambiguous configurations for any number of lines and planes. These configurations have several solutions in theory, which makes the correct solution may come from a local minimizer. Our algorithm is efficient and able to reveal local minimizers. We employ the Cayley-Gibbs-Rodriguez (CGR) parameterization of the rotation to derive a general rational cost for the three cases of 3D correspondences. The main contribution of this paper is to solve the resulting equation system of the minimal problem and the first-order optimality conditions of the least-squares problem, both of which are of complicated rational forms. The central idea of our algorithm is to introduce intermediate unknowns to simplify the problem. Extensive experimental results show that our algorithm significantly outperforms previous algorithms when the number of correspondences is small. Besides, when the global minimizer is the solution, our algorithm achieves the same accuracy as previous algorithms that have guaranteed global optimality, but our algorithm is applicable to real-time applications.
Unsupervised Learning of Monocular Depth Estimation with Bundle Adjustment, Super-Resolution and Clip Loss
Dec 08, 2018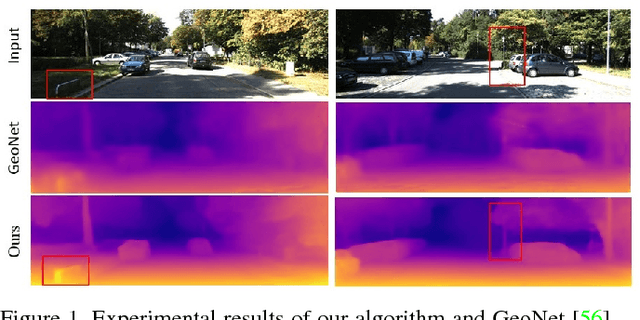
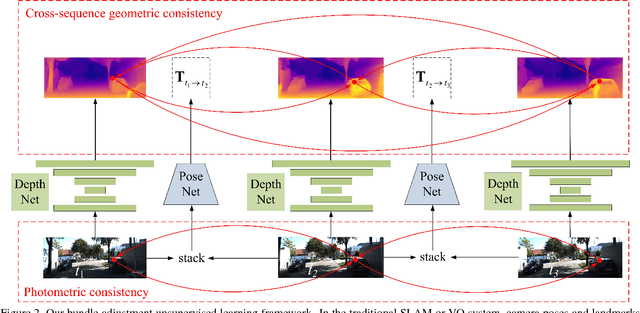
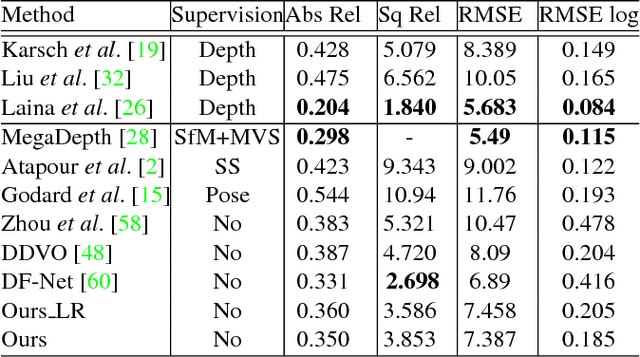
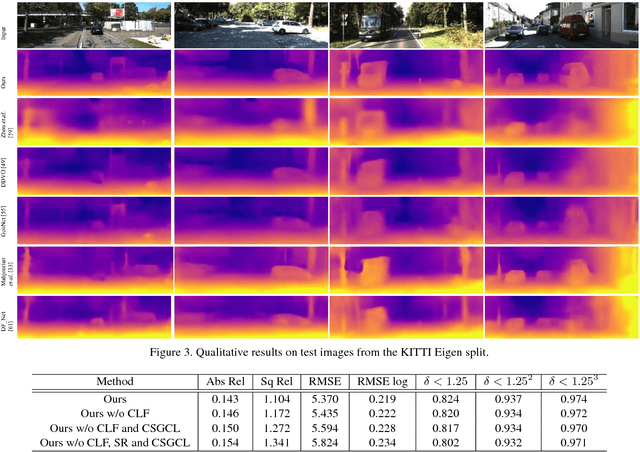
Abstract:We present a novel unsupervised learning framework for single view depth estimation using monocular videos. It is well known in 3D vision that enlarging the baseline can increase the depth estimation accuracy, and jointly optimizing a set of camera poses and landmarks is essential. In previous monocular unsupervised learning frameworks, only part of the photometric and geometric constraints within a sequence are used as supervisory signals. This may result in a short baseline and overfitting. Besides, previous works generally estimate a low resolution depth from a low resolution impute image. The low resolution depth is then interpolated to recover the original resolution. This strategy may generate large errors on object boundaries, as the depth of background and foreground are mixed to yield the high resolution depth. In this paper, we introduce a bundle adjustment framework and a super-resolution network to solve the above two problems. In bundle adjustment, depths and poses of an image sequence are jointly optimized, which increases the baseline by establishing the relationship between farther frames. The super resolution network learns to estimate a high resolution depth from a low resolution image. Additionally, we introduce the clip loss to deal with moving objects and occlusion. Experimental results on the KITTI dataset show that the proposed algorithm outperforms the state-of-the-art unsupervised methods using monocular sequences, and achieves comparable or even better result compared to unsupervised methods using stereo sequences.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge