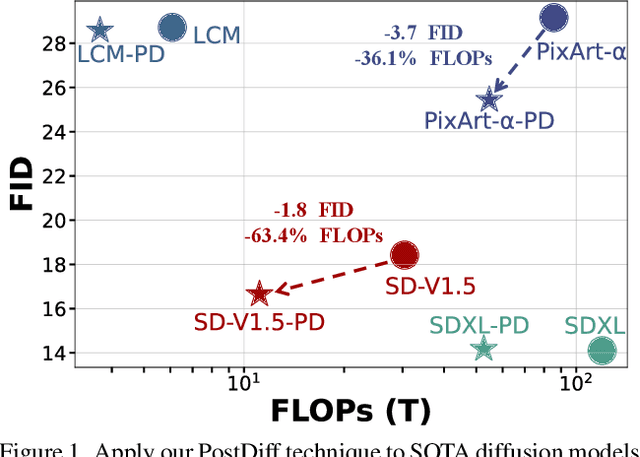
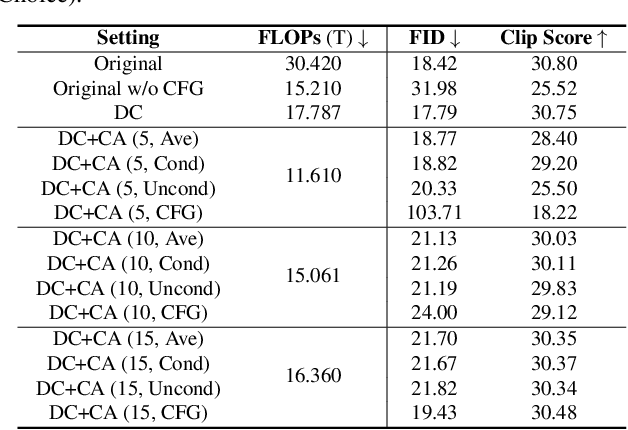
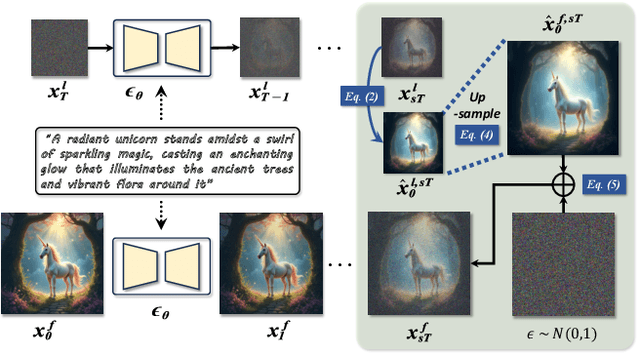
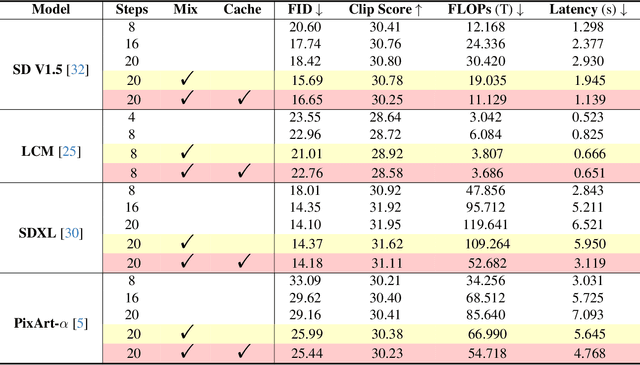
Fewer Denoising Steps or Cheaper Per-Step Inference: Towards Compute-Optimal Diffusion Model Deployment

Diffusion models have shown remarkable success across generative tasks, yet their high computational demands challenge deployment on resource-limited platforms. This paper investigates a critical question for compute-optimal diffusion model deployment: Under a post-training setting without fine-tuning, is it more effective to reduce the number of denoising steps or to use a cheaper per-step inference? Intuitively, reducing the number of denoising steps increases the variability of the distributions across steps, making the model more sensitive to compression. In contrast, keeping more denoising steps makes the differences smaller, preserving redundancy, and making post-training compression more feasible. To systematically examine this, we propose PostDiff, a training-free framework for accelerating pre-trained diffusion models by reducing redundancy at both the input level and module level in a post-training manner. At the input level, we propose a mixed-resolution denoising scheme based on the insight that reducing generation resolution in early denoising steps can enhance low-frequency components and improve final generation fidelity. At the module level, we employ a hybrid module caching strategy to reuse computations across denoising steps. Extensive experiments and ablation studies demonstrate that (1) PostDiff can significantly improve the fidelity-efficiency trade-off of state-of-the-art diffusion models, and (2) to boost efficiency while maintaining decent generation fidelity, reducing per-step inference cost is often more effective than reducing the number of denoising steps. Our code is available at https://github.com/GATECH-EIC/PostDiff.

HunyuanWorld 1.0: Generating Immersive, Explorable, and Interactive 3D Worlds from Words or Pixels

Creating immersive and playable 3D worlds from texts or images remains a fundamental challenge in computer vision and graphics. Existing world generation approaches typically fall into two categories: video-based methods that offer rich diversity but lack 3D consistency and rendering efficiency, and 3D-based methods that provide geometric consistency but struggle with limited training data and memory-inefficient representations. To address these limitations, we present HunyuanWorld 1.0, a novel framework that combines the best of both worlds for generating immersive, explorable, and interactive 3D scenes from text and image conditions. Our approach features three key advantages: 1) 360{\deg} immersive experiences via panoramic world proxies; 2) mesh export capabilities for seamless compatibility with existing computer graphics pipelines; 3) disentangled object representations for augmented interactivity. The core of our framework is a semantically layered 3D mesh representation that leverages panoramic images as 360{\deg} world proxies for semantic-aware world decomposition and reconstruction, enabling the generation of diverse 3D worlds. Extensive experiments demonstrate that our method achieves state-of-the-art performance in generating coherent, explorable, and interactive 3D worlds while enabling versatile applications in virtual reality, physical simulation, game development, and interactive content creation.

Hunyuan3D 2.1: From Images to High-Fidelity 3D Assets with Production-Ready PBR Material

3D AI-generated content (AIGC) is a passionate field that has significantly accelerated the creation of 3D models in gaming, film, and design. Despite the development of several groundbreaking models that have revolutionized 3D generation, the field remains largely accessible only to researchers, developers, and designers due to the complexities involved in collecting, processing, and training 3D models. To address these challenges, we introduce Hunyuan3D 2.1 as a case study in this tutorial. This tutorial offers a comprehensive, step-by-step guide on processing 3D data, training a 3D generative model, and evaluating its performance using Hunyuan3D 2.1, an advanced system for producing high-resolution, textured 3D assets. The system comprises two core components: the Hunyuan3D-DiT for shape generation and the Hunyuan3D-Paint for texture synthesis. We will explore the entire workflow, including data preparation, model architecture, training strategies, evaluation metrics, and deployment. By the conclusion of this tutorial, you will have the knowledge to finetune or develop a robust 3D generative model suitable for applications in gaming, virtual reality, and industrial design.

Scaling Down Text Encoders of Text-to-Image Diffusion Models

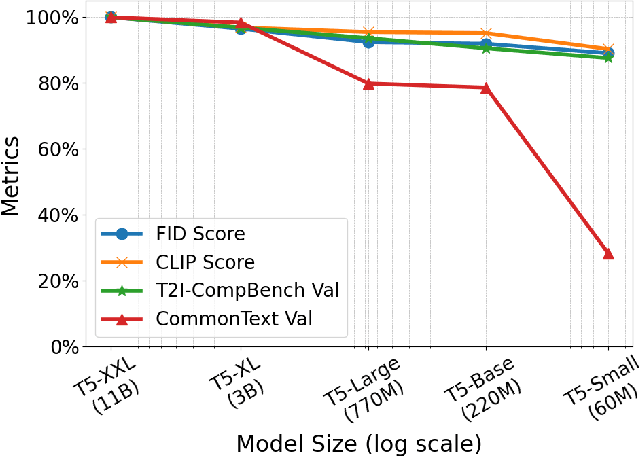
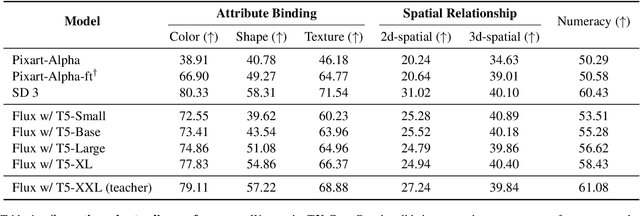
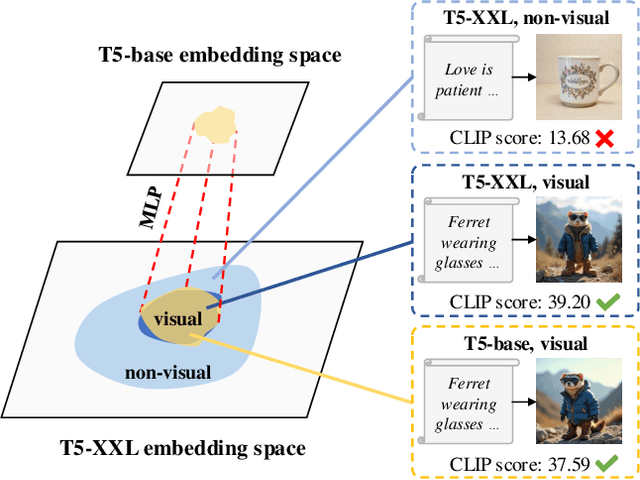
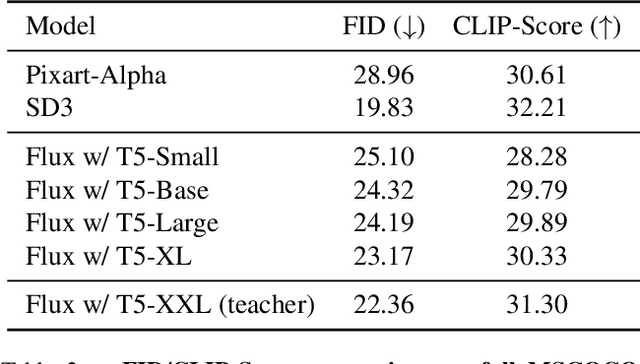
Text encoders in diffusion models have rapidly evolved, transitioning from CLIP to T5-XXL. Although this evolution has significantly enhanced the models' ability to understand complex prompts and generate text, it also leads to a substantial increase in the number of parameters. Despite T5 series encoders being trained on the C4 natural language corpus, which includes a significant amount of non-visual data, diffusion models with T5 encoder do not respond to those non-visual prompts, indicating redundancy in representational power. Therefore, it raises an important question: "Do we really need such a large text encoder?" In pursuit of an answer, we employ vision-based knowledge distillation to train a series of T5 encoder models. To fully inherit its capabilities, we constructed our dataset based on three criteria: image quality, semantic understanding, and text-rendering. Our results demonstrate the scaling down pattern that the distilled T5-base model can generate images of comparable quality to those produced by T5-XXL, while being 50 times smaller in size. This reduction in model size significantly lowers the GPU requirements for running state-of-the-art models such as FLUX and SD3, making high-quality text-to-image generation more accessible.

Hunyuan3D 2.0: Scaling Diffusion Models for High Resolution Textured 3D Assets Generation

We present Hunyuan3D 2.0, an advanced large-scale 3D synthesis system for generating high-resolution textured 3D assets. This system includes two foundation components: a large-scale shape generation model -- Hunyuan3D-DiT, and a large-scale texture synthesis model -- Hunyuan3D-Paint. The shape generative model, built on a scalable flow-based diffusion transformer, aims to create geometry that properly aligns with a given condition image, laying a solid foundation for downstream applications. The texture synthesis model, benefiting from strong geometric and diffusion priors, produces high-resolution and vibrant texture maps for either generated or hand-crafted meshes. Furthermore, we build Hunyuan3D-Studio -- a versatile, user-friendly production platform that simplifies the re-creation process of 3D assets. It allows both professional and amateur users to manipulate or even animate their meshes efficiently. We systematically evaluate our models, showing that Hunyuan3D 2.0 outperforms previous state-of-the-art models, including the open-source models and closed-source models in geometry details, condition alignment, texture quality, and etc. Hunyuan3D 2.0 is publicly released in order to fill the gaps in the open-source 3D community for large-scale foundation generative models. The code and pre-trained weights of our models are available at: https://github.com/Tencent/Hunyuan3D-2

Tencent Hunyuan3D-1.0: A Unified Framework for Text-to-3D and Image-to-3D Generation

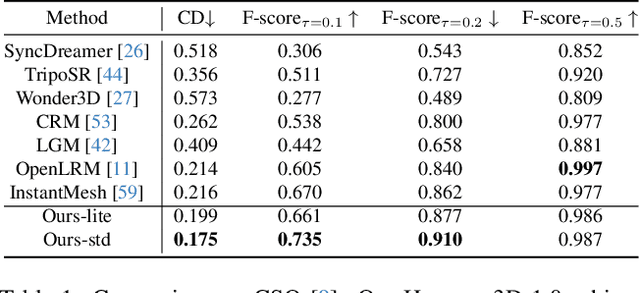
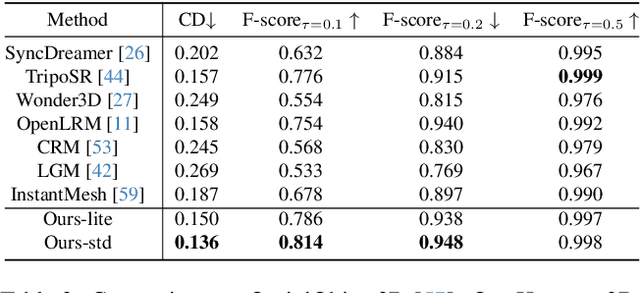
While 3D generative models have greatly improved artists' workflows, the existing diffusion models for 3D generation suffer from slow generation and poor generalization. To address this issue, we propose a two-stage approach named Hunyuan3D-1.0 including a lite version and a standard version, that both support text- and image-conditioned generation. In the first stage, we employ a multi-view diffusion model that efficiently generates multi-view RGB in approximately 4 seconds. These multi-view images capture rich details of the 3D asset from different viewpoints, relaxing the tasks from single-view to multi-view reconstruction. In the second stage, we introduce a feed-forward reconstruction model that rapidly and faithfully reconstructs the 3D asset given the generated multi-view images in approximately 7 seconds. The reconstruction network learns to handle noises and in-consistency introduced by the multi-view diffusion and leverages the available information from the condition image to efficiently recover the 3D structure. Our framework involves the text-to-image model, i.e., Hunyuan-DiT, making it a unified framework to support both text- and image-conditioned 3D generation. Our standard version has 3x more parameters than our lite and other existing model. Our Hunyuan3D-1.0 achieves an impressive balance between speed and quality, significantly reducing generation time while maintaining the quality and diversity of the produced assets.

Can Gradient Descent Provably Learn Linear Dynamic Systems?

We study the learning ability of linear recurrent neural networks with gradient descent. We prove the first theoretical guarantee on linear RNNs with Gradient Descent to learn any stable linear dynamic system. We show that despite the non-convexity of the optimization loss if the width of the RNN is large enough (and the required width in hidden layers does not rely on the length of the input sequence), a linear RNN can provably learn any stable linear dynamic system with the sample and time complexity polynomial in $\frac{1}{1-\rho_C}$ where $\rho_C$ is roughly the spectral radius of the stable system. Our results provide the first theoretical guarantee to learn a linear RNN and demonstrate how can the recurrent structure help to learn a dynamic system.

On the Provable Generalization of Recurrent Neural Networks

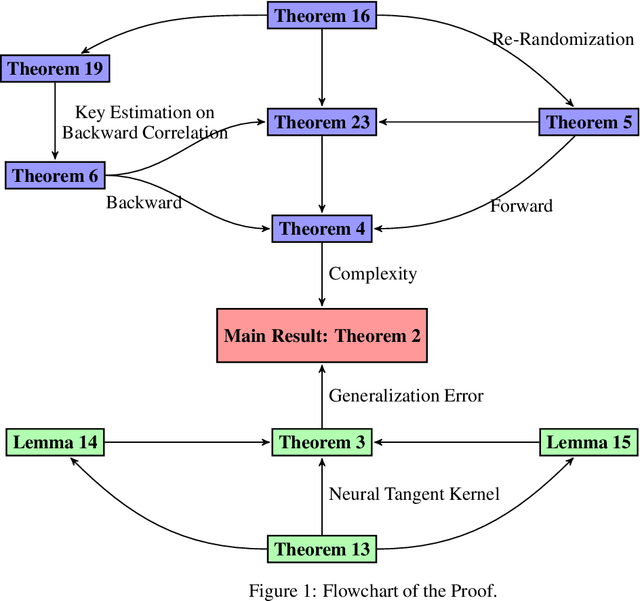
Recurrent Neural Network (RNN) is a fundamental structure in deep learning. Recently, some works study the training process of over-parameterized neural networks, and show that over-parameterized networks can learn functions in some notable concept classes with a provable generalization error bound. In this paper, we analyze the training and generalization for RNNs with random initialization, and provide the following improvements over recent works: 1) For a RNN with input sequence $x=(X_1,X_2,...,X_L)$, previous works study to learn functions that are summation of $f(\beta^T_lX_l)$ and require normalized conditions that $||X_l||\leq\epsilon$ with some very small $\epsilon$ depending on the complexity of $f$. In this paper, using detailed analysis about the neural tangent kernel matrix, we prove a generalization error bound to learn such functions without normalized conditions and show that some notable concept classes are learnable with the numbers of iterations and samples scaling almost-polynomially in the input length $L$. 2) Moreover, we prove a novel result to learn N-variables functions of input sequence with the form $f(\beta^T[X_{l_1},...,X_{l_N}])$, which do not belong to the ``additive'' concept class, i,e., the summation of function $f(X_l)$. And we show that when either $N$ or $l_0=\max(l_1,..,l_N)-\min(l_1,..,l_N)$ is small, $f(\beta^T[X_{l_1},...,X_{l_N}])$ will be learnable with the number iterations and samples scaling almost-polynomially in the input length $L$.

Is the Skip Connection Provable to Reform the Neural Network Loss Landscape?

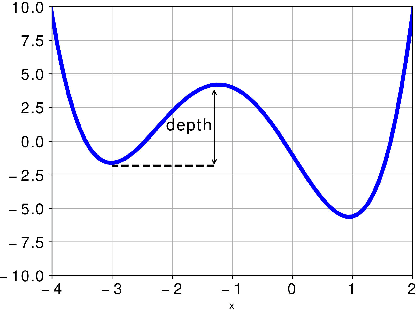
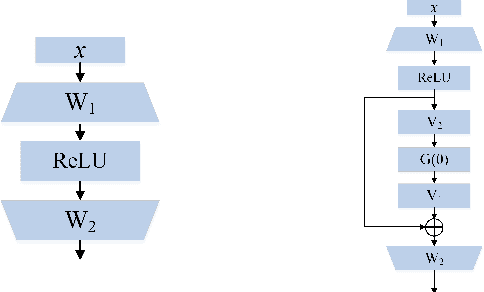
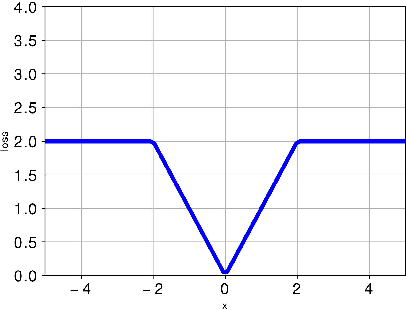
The residual network is now one of the most effective structures in deep learning, which utilizes the skip connections to ``guarantee" the performance will not get worse. However, the non-convexity of the neural network makes it unclear whether the skip connections do provably improve the learning ability since the nonlinearity may create many local minima. In some previous works \cite{freeman2016topology}, it is shown that despite the non-convexity, the loss landscape of the two-layer ReLU network has good properties when the number $m$ of hidden nodes is very large. In this paper, we follow this line to study the topology (sub-level sets) of the loss landscape of deep ReLU neural networks with a skip connection and theoretically prove that the skip connection network inherits the good properties of the two-layer network and skip connections can help to control the connectedness of the sub-level sets, such that any local minima worse than the global minima of some two-layer ReLU network will be very ``shallow". The ``depth" of these local minima are at most $O(m^{(\eta-1)/n})$, where $n$ is the input dimension, $\eta<1$. This provides a theoretical explanation for the effectiveness of the skip connection in deep learning.

On the Convergence of Perturbed Distributed Asynchronous Stochastic Gradient Descent to Second Order Stationary Points in Non-convex Optimization

In this paper, the second order convergence of non-convex optimization in the asynchronous stochastic gradient descent (ASGD) algorithm is studied systematically. We investigate the behavior of ASGD near and away from saddle points. Different from the general stochastic gradient descent(SGD), we show that ASGD might return back even if it has escaped the saddle points, yet after staying near a strict saddle point for a long enough time ($O(T)$), ASGD will finally go away from strict saddle points. An inequality is given to describe the process of ASGD to escape saddle points. Using a novel Razumikhin-Lyapunov method, we show the exponential instability of the perturbed gradient dynamics near the strict saddle points and give a more detailed estimation about how the time delay parameter $T$ influences the speed to escape. In particular, we consider the optimization of smooth nonconvex functions, and propose a perturbed asynchronous stochastic gradient descent algorithm with guarantee of convergence to second order stationary points with high probability in $O(1/\epsilon^4)$ iterations. To the best of our knowledge, this is the first work on the second order convergence of asynchronous algorithm.