Is the Skip Connection Provable to Reform the Neural Network Loss Landscape?
Paper and Code
Jun 10, 2020
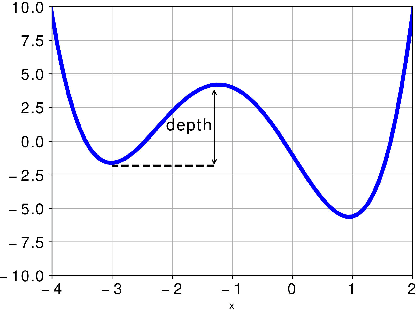
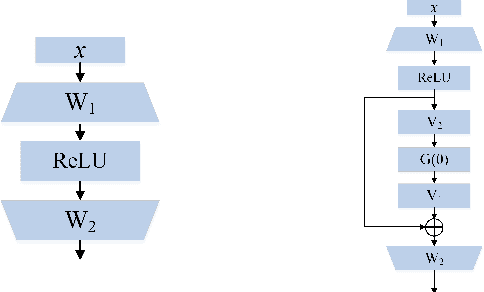
The residual network is now one of the most effective structures in deep learning, which utilizes the skip connections to ``guarantee" the performance will not get worse. However, the non-convexity of the neural network makes it unclear whether the skip connections do provably improve the learning ability since the nonlinearity may create many local minima. In some previous works \cite{freeman2016topology}, it is shown that despite the non-convexity, the loss landscape of the two-layer ReLU network has good properties when the number $m$ of hidden nodes is very large. In this paper, we follow this line to study the topology (sub-level sets) of the loss landscape of deep ReLU neural networks with a skip connection and theoretically prove that the skip connection network inherits the good properties of the two-layer network and skip connections can help to control the connectedness of the sub-level sets, such that any local minima worse than the global minima of some two-layer ReLU network will be very ``shallow". The ``depth" of these local minima are at most $O(m^{(\eta-1)/n})$, where $n$ is the input dimension, $\eta<1$. This provides a theoretical explanation for the effectiveness of the skip connection in deep learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge