Can Gradient Descent Provably Learn Linear Dynamic Systems?

We study the learning ability of linear recurrent neural networks with gradient descent. We prove the first theoretical guarantee on linear RNNs with Gradient Descent to learn any stable linear dynamic system. We show that despite the non-convexity of the optimization loss if the width of the RNN is large enough (and the required width in hidden layers does not rely on the length of the input sequence), a linear RNN can provably learn any stable linear dynamic system with the sample and time complexity polynomial in $\frac{1}{1-\rho_C}$ where $\rho_C$ is roughly the spectral radius of the stable system. Our results provide the first theoretical guarantee to learn a linear RNN and demonstrate how can the recurrent structure help to learn a dynamic system.

On the Provable Generalization of Recurrent Neural Networks

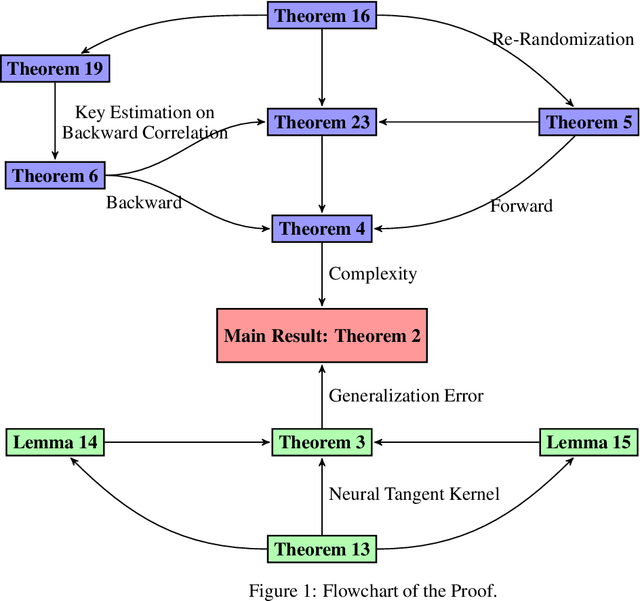
Recurrent Neural Network (RNN) is a fundamental structure in deep learning. Recently, some works study the training process of over-parameterized neural networks, and show that over-parameterized networks can learn functions in some notable concept classes with a provable generalization error bound. In this paper, we analyze the training and generalization for RNNs with random initialization, and provide the following improvements over recent works: 1) For a RNN with input sequence $x=(X_1,X_2,...,X_L)$, previous works study to learn functions that are summation of $f(\beta^T_lX_l)$ and require normalized conditions that $||X_l||\leq\epsilon$ with some very small $\epsilon$ depending on the complexity of $f$. In this paper, using detailed analysis about the neural tangent kernel matrix, we prove a generalization error bound to learn such functions without normalized conditions and show that some notable concept classes are learnable with the numbers of iterations and samples scaling almost-polynomially in the input length $L$. 2) Moreover, we prove a novel result to learn N-variables functions of input sequence with the form $f(\beta^T[X_{l_1},...,X_{l_N}])$, which do not belong to the ``additive'' concept class, i,e., the summation of function $f(X_l)$. And we show that when either $N$ or $l_0=\max(l_1,..,l_N)-\min(l_1,..,l_N)$ is small, $f(\beta^T[X_{l_1},...,X_{l_N}])$ will be learnable with the number iterations and samples scaling almost-polynomially in the input length $L$.

Coarse-grained decomposition and fine-grained interaction for multi-hop question answering

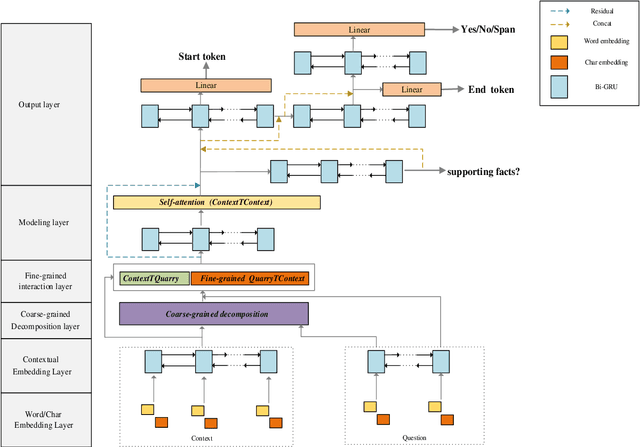
Recent advances regarding question answering and reading comprehension have resulted in models that surpass human performance when the answer is contained in a single, continuous passage of text, requiring only single-hop reasoning. However, in actual scenarios, lots of complex queries require multi-hop reasoning. The key to the Question Answering task is semantic feature interaction between documents and questions, which is widely processed by Bi-directional Attention Flow (Bi-DAF), but Bi-DAF generally captures only the surface semantics of words in complex questions and fails to capture implied semantic feature of intermediate answers. As a result, Bi-DAF partially ignores part of the contexts related to the question and cannot extract the most important parts of multiple documents. In this paper we propose a new model architecture for multi-hop question answering, by applying two completion strategies: (1) Coarse-Grain complex question Decomposition (CGDe) strategy are introduced to decompose complex question into simple ones under the condition of without any additional annotations (2) Fine-Grained Interaction (FGIn) strategy are introduced to better represent each word in the document and extract more comprehensive and accurate sentences related to the inference path. The above two strategies are combined and tested on the SQuAD and HotpotQA datasets, and the experimental results show that our method outperforms state-of-the-art baselines.