Jingyu Chen
Performance Analysis of Wireless-Powered Pinching Antenna Systems
Nov 05, 2025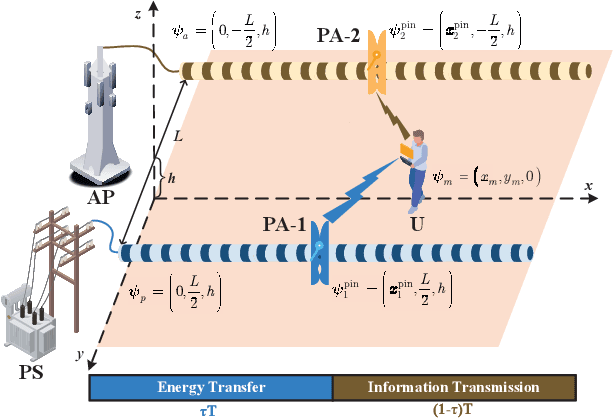
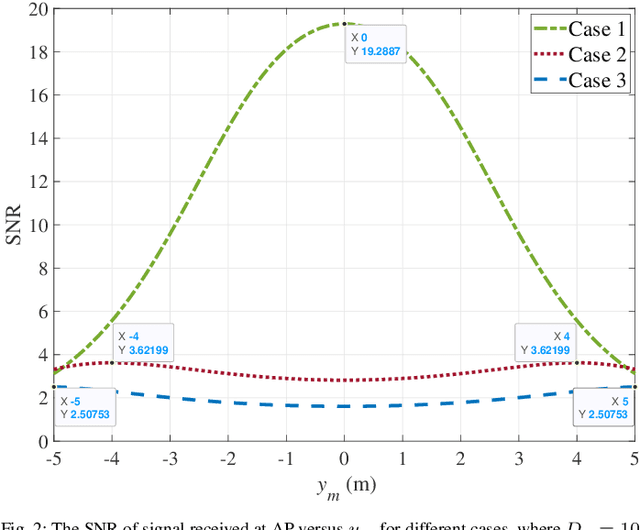
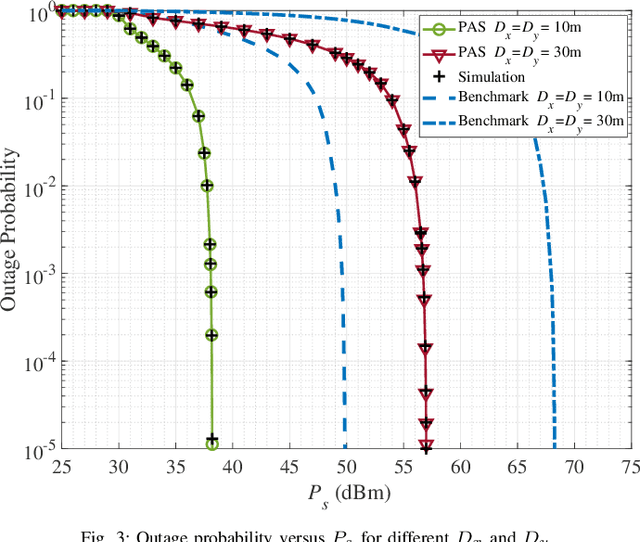
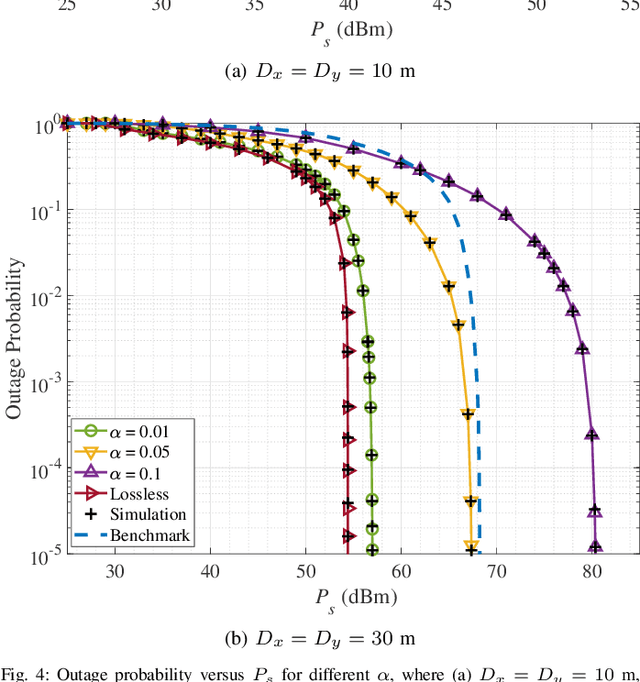
Abstract:Pinching antenna system (PAS) serves as a groundbreaking paradigm that enhances wireless communications by flexibly adjusting the position of pinching antenna (PA) and establishing a strong line-of-sight (LoS) link, thereby reducing the free-space path loss. This paper introduces the concept of wireless-powered PAS, and investigates the reliability of wireless-powered PAS to explore the advantages of PA in improving the performance of wireless-powered communication (WPC) system. In addition, we derive the closed-form expressions of outage probability and ergodic rate for the practical lossy waveguide case and ideal lossless waveguide case, respectively, and analyze the optimal deployment of waveguides and user to provide valuable insights for guiding their deployments. The results show that an increase in the absorption coefficient and in the dimensions of the user area leads to higher in-waveguide and free-space propagation losses, respectively, which in turn increase the outage probability and reduce the ergodic rate of the wireless-powered PAS. However, the performance of wireless-powered PAS is severely affected by the absorption coefficient and the waveguide length, e.g., under conditions of high absorption coefficient and long waveguide, the outage probability of wireless-powered PAS is even worse than that of traditional WPC system. While the ergodic rate of wireless-powered PAS is better than that of traditional WPC system under conditions of high absorption coefficient and long waveguide. Interestingly, the wireless-powered PAS has the optimal time allocation factor and optimal distance between power station (PS) and access point (AP) to minimize the outage probability or maximize the ergodic rate. Moreover, the system performance of PS and AP separated at the optimal distance between PS and AP is superior to that of PS and AP integrated into a hybrid access point.
A General Infrastructure and Workflow for Quadrotor Deep Reinforcement Learning and Reality Deployment
Apr 21, 2025Abstract:Deploying robot learning methods to a quadrotor in unstructured outdoor environments is an exciting task. Quadrotors operating in real-world environments by learning-based methods encounter several challenges: a large amount of simulator generated data required for training, strict demands for real-time processing onboard, and the sim-to-real gap caused by dynamic and noisy conditions. Current works have made a great breakthrough in applying learning-based methods to end-to-end control of quadrotors, but rarely mention the infrastructure system training from scratch and deploying to reality, which makes it difficult to reproduce methods and applications. To bridge this gap, we propose a platform that enables the seamless transfer of end-to-end deep reinforcement learning (DRL) policies. We integrate the training environment, flight dynamics control, DRL algorithms, the MAVROS middleware stack, and hardware into a comprehensive workflow and architecture that enables quadrotors' policies to be trained from scratch to real-world deployment in several minutes. Our platform provides rich types of environments including hovering, dynamic obstacle avoidance, trajectory tracking, balloon hitting, and planning in unknown environments, as a physical experiment benchmark. Through extensive empirical validation, we demonstrate the efficiency of proposed sim-to-real platform, and robust outdoor flight performance under real-world perturbations. Details can be found from our website https://emnavi.tech/AirGym/.
Secure Wireless-Powered zeRIS Communications
Mar 10, 2025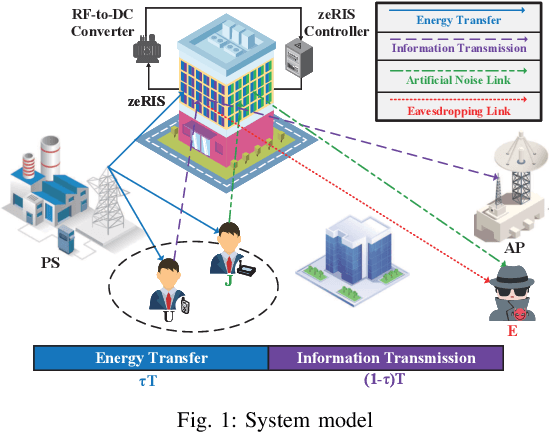
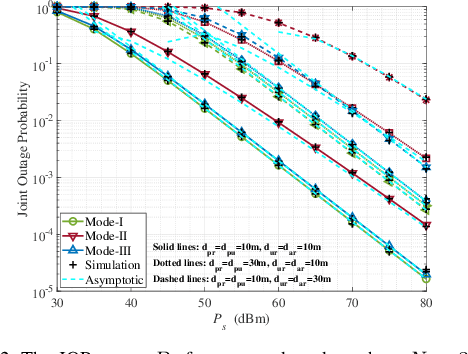
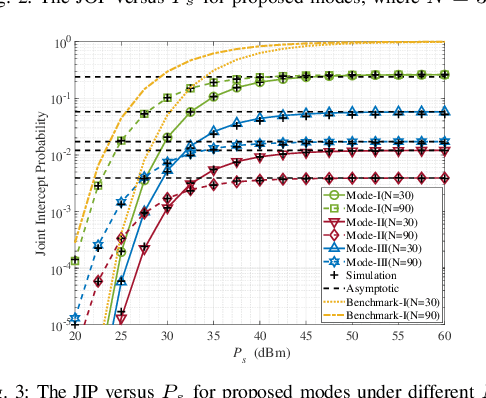
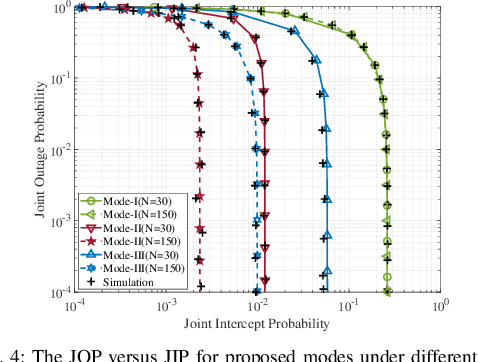
Abstract:This paper introduces the concept of wireless-powered zero-energy reconfigurable intelligent surface (zeRIS), and investigates a wireless-powered zeRIS aided communication system in terms of security, reliability and energy efficiency. In particular, we propose three new wireless-powered zeRIS modes: 1) in mode-I, N reconfigurable reflecting elements are adjusted to the optimal phase shift design of information user to maximize the reliability of the system; 2) in mode-II, N reconfigurable reflecting elements are adjusted to the optimal phase shift design of cooperative jamming user to maximize the security of the system; 3) in mode-III, N1 and N2 (N1+N2=N) reconfigurable reflecting elements are respectively adjusted to the optimal phase shift designs of information user and cooperative jamming user to balance the reliability and security of the system. Then, we propose three new metrics, i.e., joint outage probability (JOP), joint intercept probability (JIP), and secrecy energy efficiency (SEE), and analyze their closed-form expressions in three modes, respectively. The results show that under high transmission power, all the diversity gains of three modes are 1, and the JOPs of mode-I, mode-II and mode-III are improved by increasing the number of zeRIS elements, which are related to N2, N, and N^2_1, respectively. In addition, mode-I achieves the best JOP, while mode-II achieves the best JIP among three modes. We exploit two security-reliability trade-off (SRT) metrics, i.e., JOP versus JIP, and normalized joint intercept and outage probability (JIOP), to reveal the SRT performance of the proposed three modes. It is obtained that mode-II outperforms the other two modes in the JOP versus JIP, while mode-III and mode-II achieve the best performance of normalized JIOP at low and high transmission power, respectively.
Enhancing Chest X-ray Classification through Knowledge Injection in Cross-Modality Learning
Feb 19, 2025Abstract:The integration of artificial intelligence in medical imaging has shown tremendous potential, yet the relationship between pre-trained knowledge and performance in cross-modality learning remains unclear. This study investigates how explicitly injecting medical knowledge into the learning process affects the performance of cross-modality classification, focusing on Chest X-ray (CXR) images. We introduce a novel Set Theory-based knowledge injection framework that generates captions for CXR images with controllable knowledge granularity. Using this framework, we fine-tune CLIP model on captions with varying levels of medical information. We evaluate the model's performance through zero-shot classification on the CheXpert dataset, a benchmark for CXR classification. Our results demonstrate that injecting fine-grained medical knowledge substantially improves classification accuracy, achieving 72.5\% compared to 49.9\% when using human-generated captions. This highlights the crucial role of domain-specific knowledge in medical cross-modality learning. Furthermore, we explore the influence of knowledge density and the use of domain-specific Large Language Models (LLMs) for caption generation, finding that denser knowledge and specialized LLMs contribute to enhanced performance. This research advances medical image analysis by demonstrating the effectiveness of knowledge injection for improving automated CXR classification, paving the way for more accurate and reliable diagnostic tools.
PieTrack: An MOT solution based on synthetic data training and self-supervised domain adaptation
Jul 22, 2022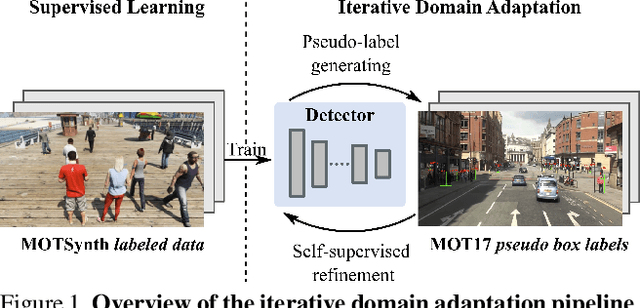
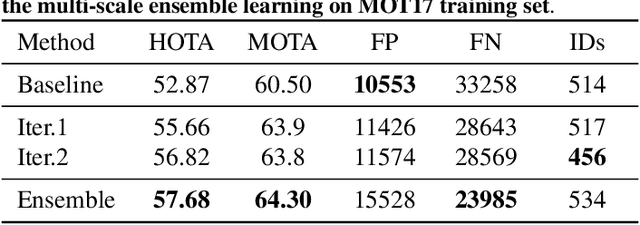
Abstract:In order to cope with the increasing demand for labeling data and privacy issues with human detection, synthetic data has been used as a substitute and showing promising results in human detection and tracking tasks. We participate in the 7th Workshop on Benchmarking Multi-Target Tracking (BMTT), themed on "How Far Can Synthetic Data Take us"? Our solution, PieTrack, is developed based on synthetic data without using any pre-trained weights. We propose a self-supervised domain adaptation method that enables mitigating the domain shift issue between the synthetic (e.g., MOTSynth) and real data (e.g., MOT17) without involving extra human labels. By leveraging the proposed multi-scale ensemble inference, we achieved a final HOTA score of 58.7 on the MOT17 testing set, ranked third place in the challenge.
UniFormer: Unified Multi-view Fusion Transformer for Spatial-Temporal Representation in Bird's-Eye-View
Jul 18, 2022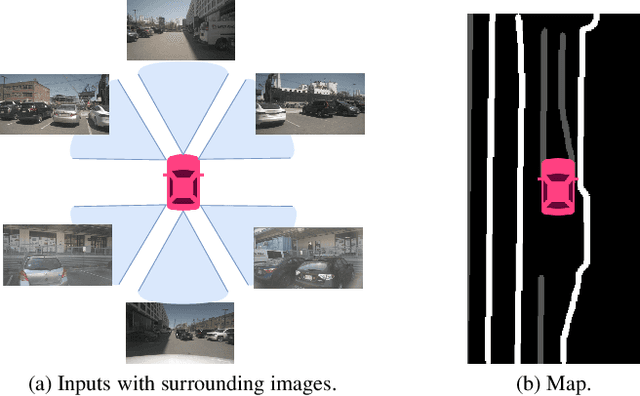

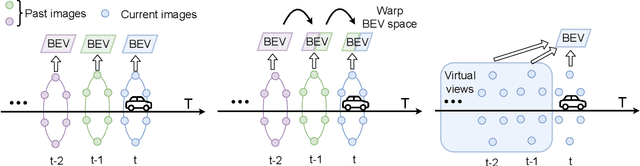
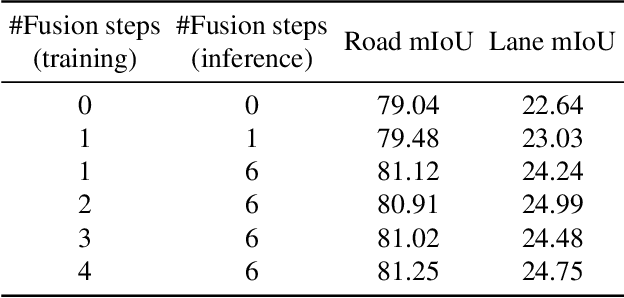
Abstract:Bird's eye view (BEV) representation is a new perception formulation for autonomous driving, which is based on spatial fusion. Further, temporal fusion is also introduced in BEV representation and gains great success. In this work, we propose a new method that unifies both spatial and temporal fusion and merges them into a unified mathematical formulation. The unified fusion could not only provide a new perspective on BEV fusion but also brings new capabilities. With the proposed unified spatial-temporal fusion, our method could support long-range fusion, which is hard to achieve in conventional BEV methods. Moreover, the BEV fusion in our work is temporal-adaptive, and the weights of temporal fusion are learnable. In contrast, conventional methods mainly use fixed and equal weights for temporal fusion. Besides, the proposed unified fusion could avoid information lost in conventional BEV fusion methods and make full use of features. Extensive experiments and ablation studies on the NuScenes dataset show the effectiveness of the proposed method and our method gains the state-of-the-art performance in the map segmentation task.
A Deep Gradient Correction Method for Iteratively Solving Linear Systems
May 22, 2022

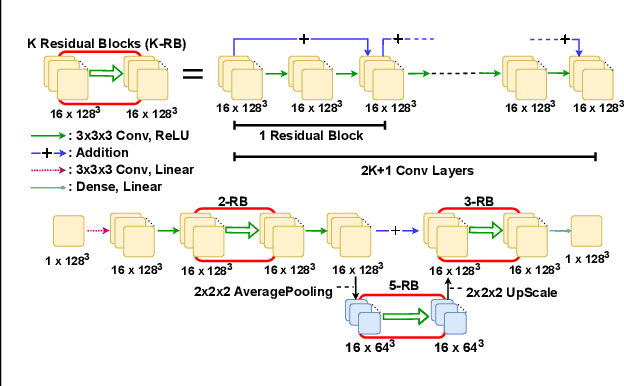

Abstract:We present a novel deep learning approach to approximate the solution of large, sparse, symmetric, positive-definite linear systems of equations. These systems arise from many problems in applied science, e.g., in numerical methods for partial differential equations. Algorithms for approximating the solution to these systems are often the bottleneck in problems that require their solution, particularly for modern applications that require many millions of unknowns. Indeed, numerical linear algebra techniques have been investigated for many decades to alleviate this computational burden. Recently, data-driven techniques have also shown promise for these problems. Motivated by the conjugate gradients algorithm that iteratively selects search directions for minimizing the matrix norm of the approximation error, we design an approach that utilizes a deep neural network to accelerate convergence via data-driven improvement of the search directions. Our method leverages a carefully chosen convolutional network to approximate the action of the inverse of the linear operator up to an arbitrary constant. We train the network using unsupervised learning with a loss function equal to the $L^2$ difference between an input and the system matrix times the network evaluation, where the unspecified constant in the approximate inverse is accounted for. We demonstrate the efficacy of our approach on spatially discretized Poisson equations with millions of degrees of freedom arising in computational fluid dynamics applications. Unlike state-of-the-art learning approaches, our algorithm is capable of reducing the linear system residual to a given tolerance in a small number of iterations, independent of the problem size. Moreover, our method generalizes effectively to various systems beyond those encountered during training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge