ASAP: Amortized Doubly-Stochastic Attention via Sliced Dual Projection

Doubly-stochastic attention has emerged as a transport-based alternative to row-softmax attention, with recent Transformer variants using it to reduce attention sinks and rank collapse while improving performance. In this family, the standard approach is Sinkhorn scaling, which trains more efficiently but still repeats matrix scaling in every inference forward pass. Sliced-transport attention removes the online iteration, but its soft sorting approximation materializes dense tensors for each slice, requiring substantially more training resources than Sinkhorn attention. We introduce ASAP: Amortized Doubly-Stochastic Attention via Sliced Dual Projection, a train-then-compile method that trains the doubly-stochastic layer with Sinkhorn, then replaces the iterative scaling loop at inference with a fixed sliced-dual operator. It learns a lightweight parametric map from exact one-dimensional Kantorovich potentials to the Sinkhorn query-side dual, then reconstructs the attention plan with a two-sided entropic c-transform. Across language and vision benchmarks, ASAP keeps the cheaper training setup and remains highly competitive with recent baselines. In the main frozen-layer benchmark, ASAP is 5.3 faster than the trained Sinkhorn teacher while matching its accuracy; in downstream replacements, ASAP recovers most of the teacher performance without any retraining.

On the Structural Failure of Chamfer Distance in 3D Shape Optimization

Chamfer distance is the standard training loss for point cloud reconstruction, completion, and generation, yet directly optimizing it can produce worse Chamfer values than not optimizing it at all. We show that this paradoxical failure is gradient-structural. The per-point Chamfer gradient creates a many-to-one collapse that is the unique attractor of the forward term and cannot be resolved by any local regularizer, including repulsion, smoothness, and density-aware re-weighting. We derive a necessary condition for collapse suppression: coupling must propagate beyond local neighborhoods. In a controlled 2D setting, shared-basis deformation suppresses collapse by providing global coupling; in 3D shape morphing, a differentiable MPM prior instantiates the same principle, consistently reducing the Chamfer gap across 20 directed pairs with a 2.5$\times$ improvement on the topologically complex dragon. The presence or absence of non-local coupling determines whether Chamfer optimization succeeds or collapses. This provides a practical design criterion for any pipeline that optimizes point-level distance metrics.

CulinaryCut-VLAP: A Vision-Language-Action-Physics Framework for Food Cutting via a Force-Aware Material Point Method

Food cutting is a highly practical yet underexplored application at the intersection of vision and robotic manipulation. The task remains challenging because interactions between the knife and deformable materials are highly nonlinear and often entail large deformations, frequent contact, and topological change, which in turn hinder stable and safe large-scale data collection. To address these challenges, we propose a unified framework that couples a vision-language-action (VLA) dataset with a physically realistic cutting simulator built on the material point method (MPM). Our simulator adopts MLS-MPM as its computational core, reducing numerical dissipation and energy drift while preserving rotational and shear responses even under topology-changing cuts. During cutting, forces and stress distributions are estimated from impulse exchanges between particles and the grid, enabling stable tracking of transient contact forces and energy transfer. We also provide a benchmark dataset that integrates diverse cutting trajectories, multi-view visual observations, and fine-grained language instructions, together with force--torque and tool--pose labels to provide physically consistent training signals. These components realize a learning--evaluation loop that respects the core physics of cutting and establishes a safe, reproducible, and scalable foundation for advancing VLA models in deformable object manipulation.

Building Machine Learning Challenges for Anomaly Detection in Science

Scientific discoveries are often made by finding a pattern or object that was not predicted by the known rules of science. Oftentimes, these anomalous events or objects that do not conform to the norms are an indication that the rules of science governing the data are incomplete, and something new needs to be present to explain these unexpected outliers. The challenge of finding anomalies can be confounding since it requires codifying a complete knowledge of the known scientific behaviors and then projecting these known behaviors on the data to look for deviations. When utilizing machine learning, this presents a particular challenge since we require that the model not only understands scientific data perfectly but also recognizes when the data is inconsistent and out of the scope of its trained behavior. In this paper, we present three datasets aimed at developing machine learning-based anomaly detection for disparate scientific domains covering astrophysics, genomics, and polar science. We present the different datasets along with a scheme to make machine learning challenges around the three datasets findable, accessible, interoperable, and reusable (FAIR). Furthermore, we present an approach that generalizes to future machine learning challenges, enabling the possibility of large, more compute-intensive challenges that can ultimately lead to scientific discovery.

Anvil: An integration of artificial intelligence, sampling techniques, and a combined CAD-CFD tool

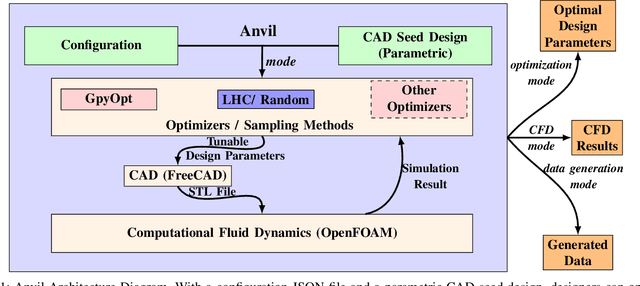
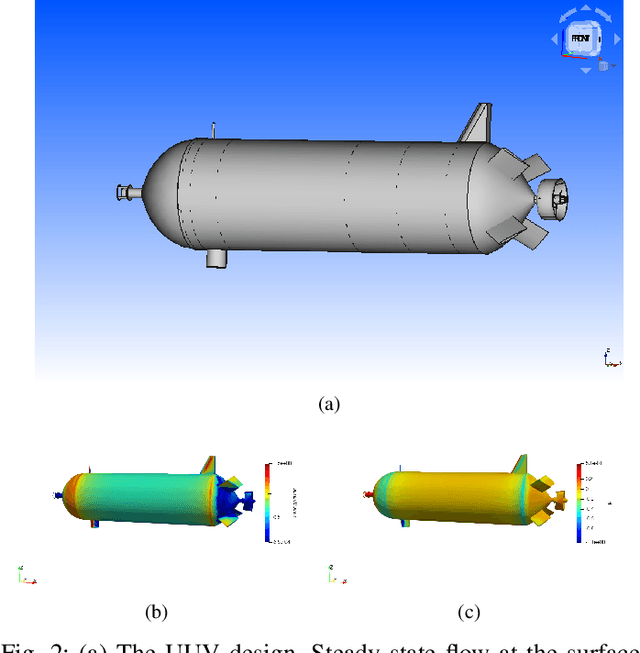
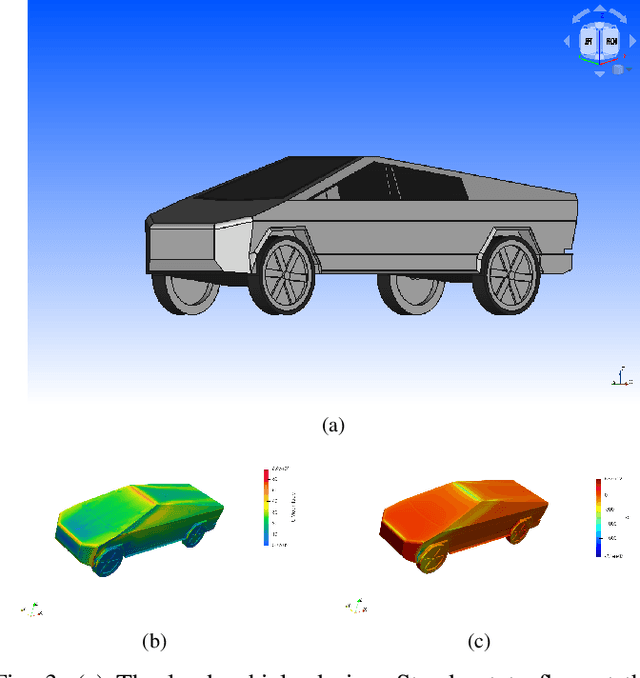
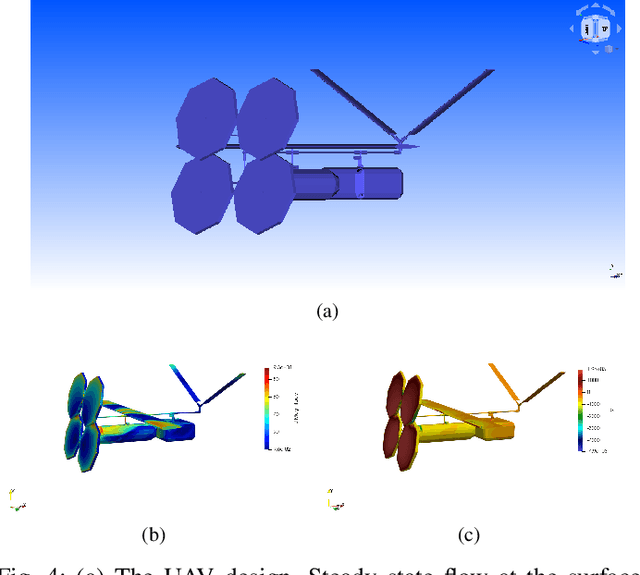
In this work, we introduce an open-source integrated CAD-CFD tool, Anvil, which combines FreeCAD for CAD modeling and OpenFOAM for CFD analysis, along with an AI-based optimization method (Bayesian optimization) and other sampling algorithms. Anvil serves as a scientific machine learning tool for shape optimization in three modes: data generation, CFD evaluation, and shape optimization. In data generation mode, it automatically runs CFD evaluations and generates data for training a surrogate model. In optimization mode, it searches for the optimal design under given requirements and optimization metrics. In CFD mode, a single CAD file can be evaluated with a single OpenFOAM run. To use Anvil, experimenters provide a JSON configuration file and a parametric CAD seed design. Anvil can be used to study solid-fluid dynamics for any subsonic flow conditions and has been demonstrated in various simulation and optimization use cases. The open-source code for the tool, installation process, artifacts (such as CAD seed designs and example STL models), experimentation results, and detailed documentation can be found at \url{https://github.com/symbench/Anvil}.

Sample-Efficient and Surrogate-Based Design Optimization of Underwater Vehicle Hulls

Physics simulations are a computational bottleneck in computer-aided design (CAD) optimization processes. Hence, in order to make accurate (computationally expensive) simulations feasible for use in design optimization, one requires either an optimization framework that is highly sample-efficient or fast data-driven proxies (surrogate models) for long running simulations. In this work, we leverage recent advances in optimization and artificial intelligence (AI) to address both of these potential solutions, in the context of designing an optimal unmanned underwater vehicle (UUV). We first investigate and compare the sample efficiency and convergence behavior of different optimization techniques with a standard computational fluid dynamics (CFD) solver in the optimization loop. We then develop a deep neural network (DNN) based surrogate model to approximate drag forces that would otherwise be computed via direct numerical simulation with the CFD solver. The surrogate model is in turn used in the optimization loop of the hull design. Our study finds that the Bayesian Optimization Lower Condition Bound (BO LCB) algorithm is the most sample-efficient optimization framework and has the best convergence behavior of those considered. Subsequently, we show that our DNN-based surrogate model predicts drag force on test data in tight agreement with CFD simulations, with a mean absolute percentage error (MAPE) of 1.85%. Combining these results, we demonstrate a two-orders-of-magnitude speedup (with comparable accuracy) for the design optimization process when the surrogate model is used. To our knowledge, this is the first study applying Bayesian optimization and DNN-based surrogate modeling to the problem of UUV design optimization, and we share our developments as open-source software.

A Deep Gradient Correction Method for Iteratively Solving Linear Systems

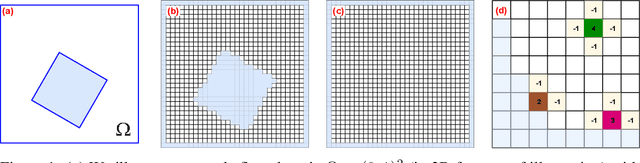
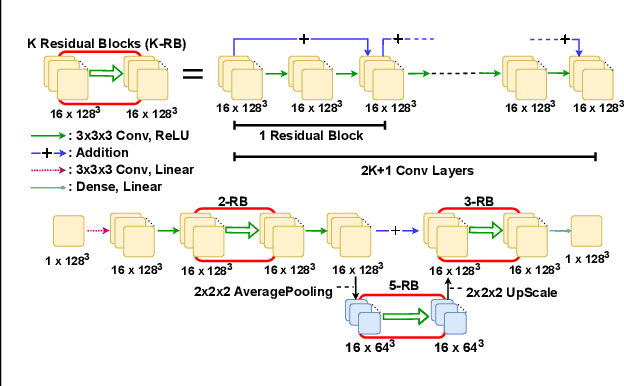
We present a novel deep learning approach to approximate the solution of large, sparse, symmetric, positive-definite linear systems of equations. These systems arise from many problems in applied science, e.g., in numerical methods for partial differential equations. Algorithms for approximating the solution to these systems are often the bottleneck in problems that require their solution, particularly for modern applications that require many millions of unknowns. Indeed, numerical linear algebra techniques have been investigated for many decades to alleviate this computational burden. Recently, data-driven techniques have also shown promise for these problems. Motivated by the conjugate gradients algorithm that iteratively selects search directions for minimizing the matrix norm of the approximation error, we design an approach that utilizes a deep neural network to accelerate convergence via data-driven improvement of the search directions. Our method leverages a carefully chosen convolutional network to approximate the action of the inverse of the linear operator up to an arbitrary constant. We train the network using unsupervised learning with a loss function equal to the $L^2$ difference between an input and the system matrix times the network evaluation, where the unspecified constant in the approximate inverse is accounted for. We demonstrate the efficacy of our approach on spatially discretized Poisson equations with millions of degrees of freedom arising in computational fluid dynamics applications. Unlike state-of-the-art learning approaches, our algorithm is capable of reducing the linear system residual to a given tolerance in a small number of iterations, independent of the problem size. Moreover, our method generalizes effectively to various systems beyond those encountered during training.