Shallow Signed Distance Functions for Kinematic Collision Bodies

We present learning-based implicit shape representations designed for real-time avatar collision queries arising in the simulation of clothing. Signed distance functions (SDFs) have been used for such queries for many years due to their computational efficiency. Recently deep neural networks have been used for implicit shape representations (DeepSDFs) due to their ability to represent multiple shapes with modest memory requirements compared to traditional representations over dense grids. However, the computational expense of DeepSDFs prevents their use in real-time clothing simulation applications. We design a learning-based representation of SDFs for human avatars whoes bodies change shape kinematically due to joint-based skinning. Rather than using a single DeepSDF for the entire avatar, we use a collection of extremely computationally efficient (shallow) neural networks that represent localized deformations arising from changes in body shape induced by the variation of a single joint. This requires a stitching process to combine each shallow SDF in the collection together into one SDF representing the signed closest distance to the boundary of the entire body. To achieve this we augment each shallow SDF with an additional output that resolves whether or not the individual shallow SDF value is referring to a closest point on the boundary of the body, or to a point on the interior of the body (but on the boundary of the individual shallow SDF). Our model is extremely fast and accurate and we demonstrate its applicability with real-time simulation of garments driven by animated characters.

A Neural-preconditioned Poisson Solver for Mixed Dirichlet and Neumann Boundary Conditions

We introduce a neural-preconditioned iterative solver for Poisson equations with mixed boundary conditions. The Poisson equation is ubiquitous in scientific computing: it governs a wide array of physical phenomena, arises as a subproblem in many numerical algorithms, and serves as a model problem for the broader class of elliptic PDEs. The most popular Poisson discretizations yield large sparse linear systems. At high resolution, and for performance-critical applications, iterative solvers can be advantageous for these -- but only when paired with powerful preconditioners. The core of our solver is a neural network trained to approximate the inverse of a discrete structured-grid Laplace operator for a domain of arbitrary shape and with mixed boundary conditions. The structure of this problem motivates a novel network architecture that we demonstrate is highly effective as a preconditioner even for boundary conditions outside the training set. We show that on challenging test cases arising from an incompressible fluid simulation, our method outperforms state-of-the-art solvers like algebraic multigrid as well as some recent neural preconditioners.

A Deep Gradient Correction Method for Iteratively Solving Linear Systems

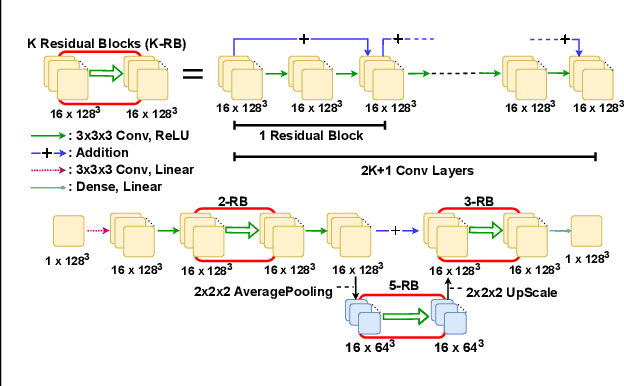
We present a novel deep learning approach to approximate the solution of large, sparse, symmetric, positive-definite linear systems of equations. These systems arise from many problems in applied science, e.g., in numerical methods for partial differential equations. Algorithms for approximating the solution to these systems are often the bottleneck in problems that require their solution, particularly for modern applications that require many millions of unknowns. Indeed, numerical linear algebra techniques have been investigated for many decades to alleviate this computational burden. Recently, data-driven techniques have also shown promise for these problems. Motivated by the conjugate gradients algorithm that iteratively selects search directions for minimizing the matrix norm of the approximation error, we design an approach that utilizes a deep neural network to accelerate convergence via data-driven improvement of the search directions. Our method leverages a carefully chosen convolutional network to approximate the action of the inverse of the linear operator up to an arbitrary constant. We train the network using unsupervised learning with a loss function equal to the $L^2$ difference between an input and the system matrix times the network evaluation, where the unspecified constant in the approximate inverse is accounted for. We demonstrate the efficacy of our approach on spatially discretized Poisson equations with millions of degrees of freedom arising in computational fluid dynamics applications. Unlike state-of-the-art learning approaches, our algorithm is capable of reducing the linear system residual to a given tolerance in a small number of iterations, independent of the problem size. Moreover, our method generalizes effectively to various systems beyond those encountered during training.

Analytically Integratable Zero-restlength Springs for Capturing Dynamic Modes unrepresented by Quasistatic Neural Networks

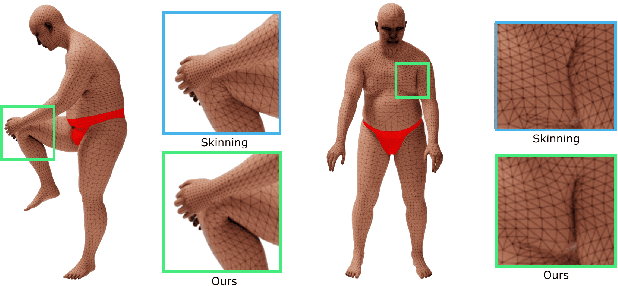
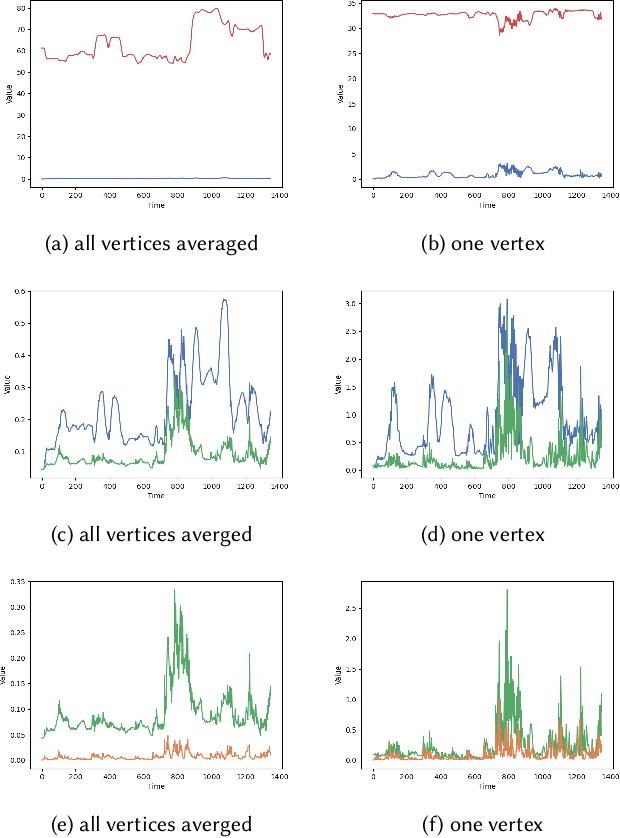
We present a novel paradigm for modeling certain types of dynamic simulation in real-time with the aid of neural networks. In order to significantly reduce the requirements on data (especially time-dependent data), as well as decrease generalization error, our approach utilizes a data-driven neural network only to capture quasistatic information (instead of dynamic or time-dependent information). Subsequently, we augment our quasistatic neural network (QNN) inference with a (real-time) dynamic simulation layer. Our key insight is that the dynamic modes lost when using a QNN approximation can be captured with a quite simple (and decoupled) zero-restlength spring model, which can be integrated analytically (as opposed to numerically) and thus has no time-step stability restrictions. Additionally, we demonstrate that the spring constitutive parameters can be robustly learned from a surprisingly small amount of dynamic simulation data. Although we illustrate the efficacy of our approach by considering soft-tissue dynamics on animated human bodies, the paradigm is extensible to many different simulation frameworks.