Julian Panetta
A Neural-preconditioned Poisson Solver for Mixed Dirichlet and Neumann Boundary Conditions
Oct 12, 2023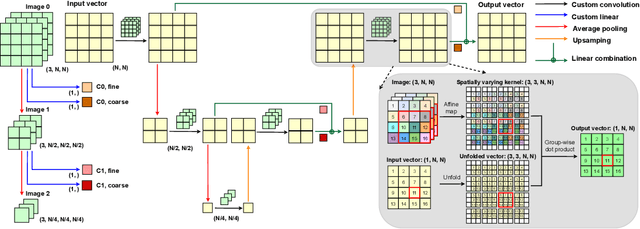

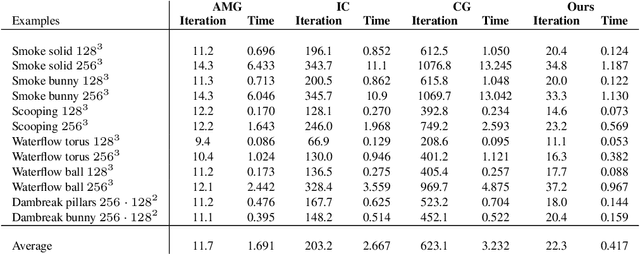

Abstract:We introduce a neural-preconditioned iterative solver for Poisson equations with mixed boundary conditions. The Poisson equation is ubiquitous in scientific computing: it governs a wide array of physical phenomena, arises as a subproblem in many numerical algorithms, and serves as a model problem for the broader class of elliptic PDEs. The most popular Poisson discretizations yield large sparse linear systems. At high resolution, and for performance-critical applications, iterative solvers can be advantageous for these -- but only when paired with powerful preconditioners. The core of our solver is a neural network trained to approximate the inverse of a discrete structured-grid Laplace operator for a domain of arbitrary shape and with mixed boundary conditions. The structure of this problem motivates a novel network architecture that we demonstrate is highly effective as a preconditioner even for boundary conditions outside the training set. We show that on challenging test cases arising from an incompressible fluid simulation, our method outperforms state-of-the-art solvers like algebraic multigrid as well as some recent neural preconditioners.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge