Beam-Plasma Collective Oscillations in Intense Charged-Particle Beams: Dielectric Response Theory, Langmuir Wave Dispersion, and Unsupervised Detection via Prometheus

We develop a theoretical and computational framework for beam-plasma collective oscillations in intense charged-particle beams at intermediate energies (10-100 MeV). In Part I, we formulate a kinetic field theory governed by the Vlasov-Poisson system, deriving the Lindhard dielectric function and random phase approximation (RPA) polarization tensor for three beam distribution functions. We prove via the dielectric function epsilon(omega,q)=0 the existence of undamped Langmuir wave modes above a critical beam density n_c, obtain explicit beam-plasma dispersion relations, and show that Landau damping vanishes above the particle-hole continuum. The plasma frequency Omega_p^2 = ne^2/(m*epsilon_0) is fixed by the f-sum rule independently of distribution shape; higher dispersion coefficients depend on velocity moments. Space charge effects drive anomalous beam broadening with sqrt(n-n_c) onset and Friedel oscillations at q=2k_F. The beam-plasma transition belongs to the 3D Ising universality class via renormalization group analysis. In Part II, we validate these predictions using Prometheus, a beta-VAE trained on static structure factor data S(q) from particle-in-cell (PIC) beam simulations. Prometheus detects collective plasma oscillation onset in Gaussian and uniform distributions, confirms their absence in the degenerate Fermi gas (n_c -> 0), and resolves the Kohn anomaly at q=2k_F. Dispersion analysis of S(q,omega) from PIC simulations verifies the distribution-independent Omega_p predicted by the f-sum rule. All six validation checks pass. Predicted signatures -- density-tunable plasma resonances at omega_p proportional to sqrt(n), anomalous beam broadening with sqrt(n-n_c) onset, and Friedel oscillations -- are accessible at existing intermediate-energy beam facilities.

Step 3.5 Flash: Open Frontier-Level Intelligence with 11B Active Parameters

We introduce Step 3.5 Flash, a sparse Mixture-of-Experts (MoE) model that bridges frontier-level agentic intelligence and computational efficiency. We focus on what matters most when building agents: sharp reasoning and fast, reliable execution. Step 3.5 Flash pairs a 196B-parameter foundation with 11B active parameters for efficient inference. It is optimized with interleaved 3:1 sliding-window/full attention and Multi-Token Prediction (MTP-3) to reduce the latency and cost of multi-round agentic interactions. To reach frontier-level intelligence, we design a scalable reinforcement learning framework that combines verifiable signals with preference feedback, while remaining stable under large-scale off-policy training, enabling consistent self-improvement across mathematics, code, and tool use. Step 3.5 Flash demonstrates strong performance across agent, coding, and math tasks, achieving 85.4% on IMO-AnswerBench, 86.4% on LiveCodeBench-v6 (2024.08-2025.05), 88.2% on tau2-Bench, 69.0% on BrowseComp (with context management), and 51.0% on Terminal-Bench 2.0, comparable to frontier models such as GPT-5.2 xHigh and Gemini 3.0 Pro. By redefining the efficiency frontier, Step 3.5 Flash provides a high-density foundation for deploying sophisticated agents in real-world industrial environments.

STEP3-VL-10B Technical Report

We present STEP3-VL-10B, a lightweight open-source foundation model designed to redefine the trade-off between compact efficiency and frontier-level multimodal intelligence. STEP3-VL-10B is realized through two strategic shifts: first, a unified, fully unfrozen pre-training strategy on 1.2T multimodal tokens that integrates a language-aligned Perception Encoder with a Qwen3-8B decoder to establish intrinsic vision-language synergy; and second, a scaled post-training pipeline featuring over 1k iterations of reinforcement learning. Crucially, we implement Parallel Coordinated Reasoning (PaCoRe) to scale test-time compute, allocating resources to scalable perceptual reasoning that explores and synthesizes diverse visual hypotheses. Consequently, despite its compact 10B footprint, STEP3-VL-10B rivals or surpasses models 10$\times$-20$\times$ larger (e.g., GLM-4.6V-106B, Qwen3-VL-235B) and top-tier proprietary flagships like Gemini 2.5 Pro and Seed-1.5-VL. Delivering best-in-class performance, it records 92.2% on MMBench and 80.11% on MMMU, while excelling in complex reasoning with 94.43% on AIME2025 and 75.95% on MathVision. We release the full model suite to provide the community with a powerful, efficient, and reproducible baseline.

MCP-RiskCue: Can LLM Infer Risk Information From MCP Server System Logs?

Large language models (LLMs) demonstrate strong capabilities in solving complex tasks when integrated with external tools. The Model Context Protocol (MCP) has become a standard interface for enabling such tool-based interactions. However, these interactions introduce substantial security concerns, particularly when the MCP server is compromised or untrustworthy. While prior benchmarks primarily focus on prompt injection attacks or analyze the vulnerabilities of LLM MCP interaction trajectories, limited attention has been given to the underlying system logs associated with malicious MCP servers. To address this gap, we present the first synthetic benchmark for evaluating LLMs ability to identify security risks from system logs. We define nine categories of MCP server risks and generate 1,800 synthetic system logs using ten state-of-the-art LLMs. These logs are embedded in the return values of 243 curated MCP servers, yielding a dataset of 2,421 chat histories for training and 471 queries for evaluation. Our pilot experiments reveal that smaller models often fail to detect risky system logs, leading to high false negatives. While models trained with supervised fine-tuning (SFT) tend to over-flag benign logs, resulting in elevated false positives, Reinforcement Learning from Verifiable Reward (RLVR) offers a better precision-recall balance. In particular, after training with Group Relative Policy Optimization (GRPO), Llama3.1-8B-Instruct achieves 83% accuracy, surpassing the best-performing large remote model by 9 percentage points. Fine-grained, per-category analysis further underscores the effectiveness of reinforcement learning in enhancing LLM safety within the MCP framework. Code and data are available at: https://github.com/PorUna-byte/MCP-RiskCue

Iterative Predictor-Critic Code Decoding for Real-World Image Dehazing

We propose a novel Iterative Predictor-Critic Code Decoding framework for real-world image dehazing, abbreviated as IPC-Dehaze, which leverages the high-quality codebook prior encapsulated in a pre-trained VQGAN. Apart from previous codebook-based methods that rely on one-shot decoding, our method utilizes high-quality codes obtained in the previous iteration to guide the prediction of the Code-Predictor in the subsequent iteration, improving code prediction accuracy and ensuring stable dehazing performance. Our idea stems from the observations that 1) the degradation of hazy images varies with haze density and scene depth, and 2) clear regions play crucial cues in restoring dense haze regions. However, it is non-trivial to progressively refine the obtained codes in subsequent iterations, owing to the difficulty in determining which codes should be retained or replaced at each iteration. Another key insight of our study is to propose Code-Critic to capture interrelations among codes. The Code-Critic is used to evaluate code correlations and then resample a set of codes with the highest mask scores, i.e., a higher score indicates that the code is more likely to be rejected, which helps retain more accurate codes and predict difficult ones. Extensive experiments demonstrate the superiority of our method over state-of-the-art methods in real-world dehazing.

Reward Shaping to Mitigate Reward Hacking in RLHF

Reinforcement Learning from Human Feedback (RLHF) is essential for aligning large language models (LLMs) with human values. However, RLHF is susceptible to reward hacking, where the agent exploits flaws in the reward function rather than learning the intended behavior, thus degrading alignment. While reward shaping helps stabilize RLHF and partially mitigate reward hacking, a systematic investigation into shaping techniques and their underlying principles remains lacking. To bridge this gap, we present a comprehensive study of the prevalent reward shaping methods. Our analysis suggests three key design principles: (1) RL reward is ideally bounded, (2) RL benefits from rapid initial growth followed by gradual convergence, and (3) RL reward is best formulated as a function of centered reward. Guided by these insights, we propose Preference As Reward (PAR), a novel approach that leverages the latent preferences embedded within the reward model itself as the signal for reinforcement learning. We evaluated PAR on two base models, Gemma2-2B and Llama3-8B, using two datasets, Ultrafeedback-Binarized and HH-RLHF. Experimental results demonstrate PAR's superior performance over other reward shaping methods. On the AlpacaEval 2.0 benchmark, PAR achieves a win rate at least 5 percentage points higher than competing approaches. Furthermore, PAR exhibits remarkable data efficiency, requiring only a single reference reward for optimal performance, and maintains robustness against reward hacking even after two full epochs of training. Code is available at https://github.com/PorUna-byte/PAR.

FaceMe: Robust Blind Face Restoration with Personal Identification

Blind face restoration is a highly ill-posed problem due to the lack of necessary context. Although existing methods produce high-quality outputs, they often fail to faithfully preserve the individual's identity. In this paper, we propose a personalized face restoration method, FaceMe, based on a diffusion model. Given a single or a few reference images, we use an identity encoder to extract identity-related features, which serve as prompts to guide the diffusion model in restoring high-quality and identity-consistent facial images. By simply combining identity-related features, we effectively minimize the impact of identity-irrelevant features during training and support any number of reference image inputs during inference. Additionally, thanks to the robustness of the identity encoder, synthesized images can be used as reference images during training, and identity changing during inference does not require fine-tuning the model. We also propose a pipeline for constructing a reference image training pool that simulates the poses and expressions that may appear in real-world scenarios. Experimental results demonstrate that our FaceMe can restore high-quality facial images while maintaining identity consistency, achieving excellent performance and robustness.

SocialGaze: Improving the Integration of Human Social Norms in Large Language Models

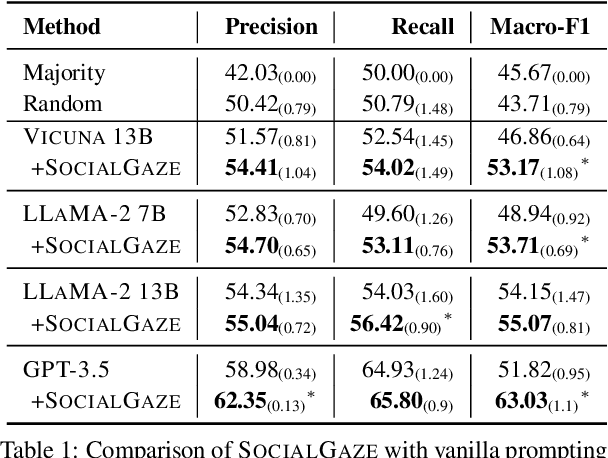
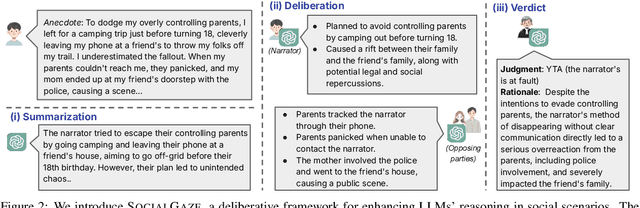
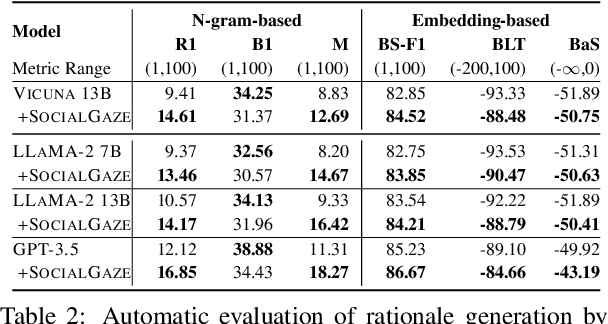
While much research has explored enhancing the reasoning capabilities of large language models (LLMs) in the last few years, there is a gap in understanding the alignment of these models with social values and norms. We introduce the task of judging social acceptance. Social acceptance requires models to judge and rationalize the acceptability of people's actions in social situations. For example, is it socially acceptable for a neighbor to ask others in the community to keep their pets indoors at night? We find that LLMs' understanding of social acceptance is often misaligned with human consensus. To alleviate this, we introduce SocialGaze, a multi-step prompting framework, in which a language model verbalizes a social situation from multiple perspectives before forming a judgment. Our experiments demonstrate that the SocialGaze approach improves the alignment with human judgments by up to 11 F1 points with the GPT-3.5 model. We also identify biases and correlations in LLMs in assigning blame that is related to features such as the gender (males are significantly more likely to be judged unfairly) and age (LLMs are more aligned with humans for older narrators).

GumbelSoft: Diversified Language Model Watermarking via the GumbelMax-trick

Large language models (LLMs) excellently generate human-like text, but also raise concerns about misuse in fake news and academic dishonesty. Decoding-based watermark, particularly the GumbelMax-trick-based watermark(GM watermark), is a standout solution for safeguarding machine-generated texts due to its notable detectability. However, GM watermark encounters a major challenge with generation diversity, always yielding identical outputs for the same prompt, negatively impacting generation diversity and user experience. To overcome this limitation, we propose a new type of GM watermark, the Logits-Addition watermark, and its three variants, specifically designed to enhance diversity. Among these, the GumbelSoft watermark (a softmax variant of the Logits-Addition watermark) demonstrates superior performance in high diversity settings, with its AUROC score outperforming those of the two alternative variants by 0.1 to 0.3 and surpassing other decoding-based watermarking methods by a minimum of 0.1.

Ask One More Time: Self-Agreement Improves Reasoning of Language Models in All Scenarios

Although chain-of-thought (CoT) prompting combined with language models has achieved encouraging results on complex reasoning tasks, the naive greedy decoding used in CoT prompting usually causes the repetitiveness and local optimality. To address this shortcoming, ensemble-optimization tries to obtain multiple reasoning paths to get the final answer assembly. However, current ensemble-optimization methods either simply employ rule-based post-processing such as \textit{self-consistency}, or train an additional model based on several task-related human annotations to select the best one among multiple reasoning paths, yet fail to generalize to realistic settings where the type of input questions is unknown or the answer format of reasoning paths is unknown. To avoid their limitations, we propose \textbf{self-agreement}, a generalizable ensemble-optimization method applying in almost all scenarios where the type of input questions and the answer format of reasoning paths may be known or unknown. Self-agreement firstly samples from language model's decoder to generate a \textit{diverse} set of reasoning paths, and subsequently prompts the language model \textit{one more time} to determine the optimal answer by selecting the most \textit{agreed} answer among the sampled reasoning paths. Self-agreement simultaneously achieves remarkable performance on six public reasoning benchmarks and superior generalization capabilities.