Ganghua Wang
Can Agentic AI Match the Performance of Human Data Scientists?
Dec 24, 2025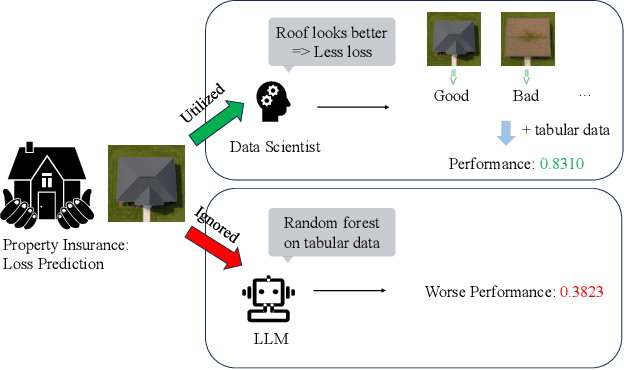

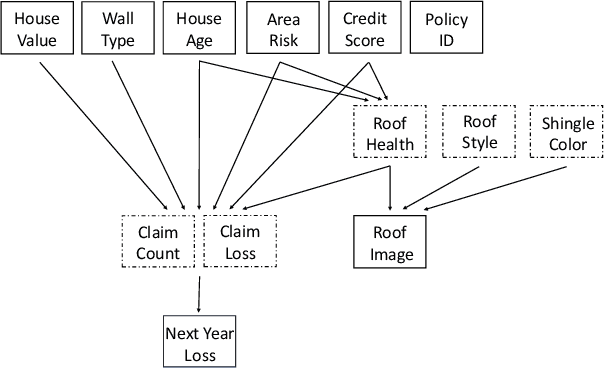

Abstract:Data science plays a critical role in transforming complex data into actionable insights across numerous domains. Recent developments in large language models (LLMs) have significantly automated data science workflows, but a fundamental question persists: Can these agentic AI systems truly match the performance of human data scientists who routinely leverage domain-specific knowledge? We explore this question by designing a prediction task where a crucial latent variable is hidden in relevant image data instead of tabular features. As a result, agentic AI that generates generic codes for modeling tabular data cannot perform well, while human experts could identify the important hidden variable using domain knowledge. We demonstrate this idea with a synthetic dataset for property insurance. Our experiments show that agentic AI that relies on generic analytics workflow falls short of methods that use domain-specific insights. This highlights a key limitation of the current agentic AI for data science and underscores the need for future research to develop agentic AI systems that can better recognize and incorporate domain knowledge.
An Outlook on the Opportunities and Challenges of Multi-Agent AI Systems
May 23, 2025Abstract:Multi-agent AI systems (MAS) offer a promising framework for distributed intelligence, enabling collaborative reasoning, planning, and decision-making across autonomous agents. This paper provides a systematic outlook on the current opportunities and challenges of MAS, drawing insights from recent advances in large language models (LLMs), federated optimization, and human-AI interaction. We formalize key concepts including agent topology, coordination protocols, and shared objectives, and identify major risks such as dependency, misalignment, and vulnerabilities arising from training data overlap. Through a biologically inspired simulation and comprehensive theoretical framing, we highlight critical pathways for developing robust, scalable, and secure MAS in real-world settings.
Ice Cream Doesn't Cause Drowning: Benchmarking LLMs Against Statistical Pitfalls in Causal Inference
May 19, 2025Abstract:Reliable causal inference is essential for making decisions in high-stakes areas like medicine, economics, and public policy. However, it remains unclear whether large language models (LLMs) can handle rigorous and trustworthy statistical causal inference. Current benchmarks usually involve simplified tasks. For example, these tasks might only ask LLMs to identify semantic causal relationships or draw conclusions directly from raw data. As a result, models may overlook important statistical pitfalls, such as Simpson's paradox or selection bias. This oversight limits the applicability of LLMs in the real world. To address these limitations, we propose CausalPitfalls, a comprehensive benchmark designed to rigorously evaluate the capability of LLMs in overcoming common causal inference pitfalls. Our benchmark features structured challenges across multiple difficulty levels, each paired with grading rubrics. This approach allows us to quantitatively measure both causal reasoning capabilities and the reliability of LLMs' responses. We evaluate models using two protocols: (1) direct prompting, which assesses intrinsic causal reasoning, and (2) code-assisted prompting, where models generate executable code for explicit statistical analysis. Additionally, we validate the effectiveness of this judge by comparing its scoring with assessments from human experts. Our results reveal significant limitations in current LLMs when performing statistical causal inference. The CausalPitfalls benchmark provides essential guidance and quantitative metrics to advance the development of trustworthy causal reasoning systems.
Cer-Eval: Certifiable and Cost-Efficient Evaluation Framework for LLMs
May 02, 2025Abstract:As foundation models continue to scale, the size of trained models grows exponentially, presenting significant challenges for their evaluation. Current evaluation practices involve curating increasingly large datasets to assess the performance of large language models (LLMs). However, there is a lack of systematic analysis and guidance on determining the sufficiency of test data or selecting informative samples for evaluation. This paper introduces a certifiable and cost-efficient evaluation framework for LLMs. Our framework adapts to different evaluation objectives and outputs confidence intervals that contain true values with high probability. We use ``test sample complexity'' to quantify the number of test points needed for a certifiable evaluation and derive tight bounds on test sample complexity. Based on the developed theory, we develop a partition-based algorithm, named Cer-Eval, that adaptively selects test points to minimize the cost of LLM evaluation. Real-world experiments demonstrate that Cer-Eval can save 20% to 40% test points across various benchmarks, while maintaining an estimation error level comparable to the current evaluation process and providing a 95% confidence guarantee.
Model Privacy: A Unified Framework to Understand Model Stealing Attacks and Defenses
Feb 21, 2025

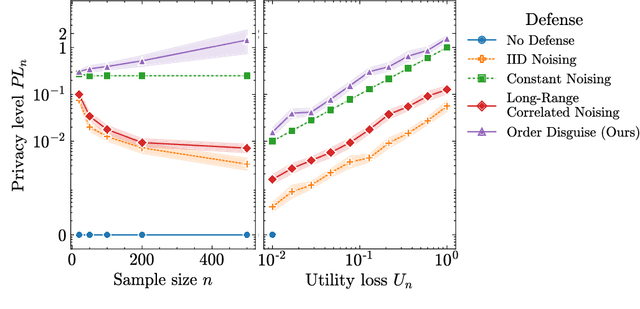
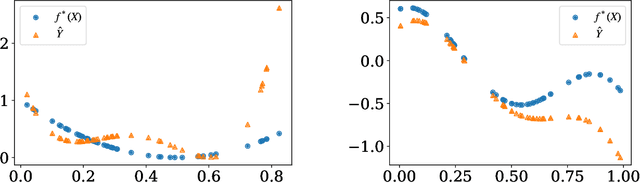
Abstract:The use of machine learning (ML) has become increasingly prevalent in various domains, highlighting the importance of understanding and ensuring its safety. One pressing concern is the vulnerability of ML applications to model stealing attacks. These attacks involve adversaries attempting to recover a learned model through limited query-response interactions, such as those found in cloud-based services or on-chip artificial intelligence interfaces. While existing literature proposes various attack and defense strategies, these often lack a theoretical foundation and standardized evaluation criteria. In response, this work presents a framework called ``Model Privacy'', providing a foundation for comprehensively analyzing model stealing attacks and defenses. We establish a rigorous formulation for the threat model and objectives, propose methods to quantify the goodness of attack and defense strategies, and analyze the fundamental tradeoffs between utility and privacy in ML models. Our developed theory offers valuable insights into enhancing the security of ML models, especially highlighting the importance of the attack-specific structure of perturbations for effective defenses. We demonstrate the application of model privacy from the defender's perspective through various learning scenarios. Extensive experiments corroborate the insights and the effectiveness of defense mechanisms developed under the proposed framework.
Drift to Remember
Sep 21, 2024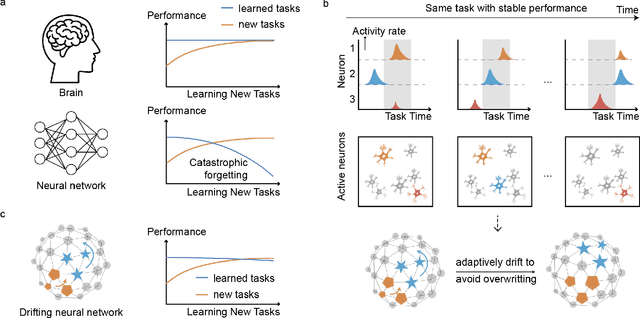
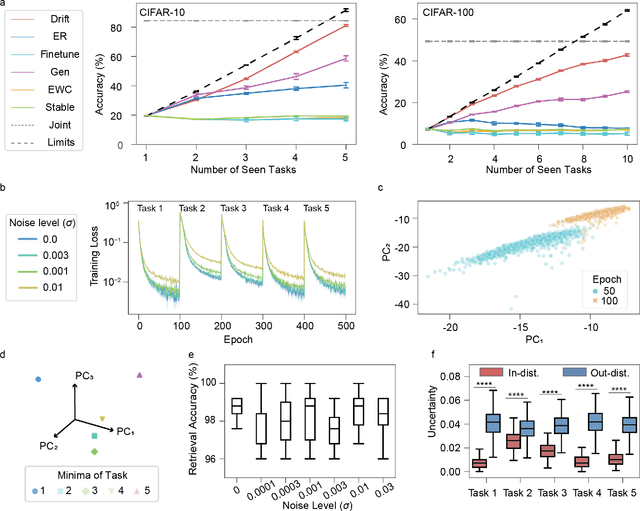
Abstract:Lifelong learning in artificial intelligence (AI) aims to mimic the biological brain's ability to continuously learn and retain knowledge, yet it faces challenges such as catastrophic forgetting. Recent neuroscience research suggests that neural activity in biological systems undergoes representational drift, where neural responses evolve over time, even with consistent inputs and tasks. We hypothesize that representational drift can alleviate catastrophic forgetting in AI during new task acquisition. To test this, we introduce DriftNet, a network designed to constantly explore various local minima in the loss landscape while dynamically retrieving relevant tasks. This approach ensures efficient integration of new information and preserves existing knowledge. Experimental studies in image classification and natural language processing demonstrate that DriftNet outperforms existing models in lifelong learning. Importantly, DriftNet is scalable in handling a sequence of tasks such as sentiment analysis and question answering using large language models (LLMs) with billions of parameters on a single Nvidia A100 GPU. DriftNet efficiently updates LLMs using only new data, avoiding the need for full dataset retraining. Tested on GPT-2 and RoBERTa, DriftNet is a robust, cost-effective solution for lifelong learning in LLMs. This study not only advances AI systems to emulate biological learning, but also provides insights into the adaptive mechanisms of biological neural systems, deepening our understanding of lifelong learning in nature.
Demystifying Poisoning Backdoor Attacks from a Statistical Perspective
Oct 18, 2023



Abstract:The growing dependence on machine learning in real-world applications emphasizes the importance of understanding and ensuring its safety. Backdoor attacks pose a significant security risk due to their stealthy nature and potentially serious consequences. Such attacks involve embedding triggers within a learning model with the intention of causing malicious behavior when an active trigger is present while maintaining regular functionality without it. This paper evaluates the effectiveness of any backdoor attack incorporating a constant trigger, by establishing tight lower and upper boundaries for the performance of the compromised model on both clean and backdoor test data. The developed theory answers a series of fundamental but previously underexplored problems, including (1) what are the determining factors for a backdoor attack's success, (2) what is the direction of the most effective backdoor attack, and (3) when will a human-imperceptible trigger succeed. Our derived understanding applies to both discriminative and generative models. We also demonstrate the theory by conducting experiments using benchmark datasets and state-of-the-art backdoor attack scenarios.
Mitigating Group Bias in Federated Learning: Beyond Local Fairness
May 17, 2023



Abstract:The issue of group fairness in machine learning models, where certain sub-populations or groups are favored over others, has been recognized for some time. While many mitigation strategies have been proposed in centralized learning, many of these methods are not directly applicable in federated learning, where data is privately stored on multiple clients. To address this, many proposals try to mitigate bias at the level of clients before aggregation, which we call locally fair training. However, the effectiveness of these approaches is not well understood. In this work, we investigate the theoretical foundation of locally fair training by studying the relationship between global model fairness and local model fairness. Additionally, we prove that for a broad class of fairness metrics, the global model's fairness can be obtained using only summary statistics from local clients. Based on that, we propose a globally fair training algorithm that directly minimizes the penalized empirical loss. Real-data experiments demonstrate the promising performance of our proposed approach for enhancing fairness while retaining high accuracy compared to locally fair training methods.
Provable Identifiability of Two-Layer ReLU Neural Networks via LASSO Regularization
May 07, 2023



Abstract:LASSO regularization is a popular regression tool to enhance the prediction accuracy of statistical models by performing variable selection through the $\ell_1$ penalty, initially formulated for the linear model and its variants. In this paper, the territory of LASSO is extended to two-layer ReLU neural networks, a fashionable and powerful nonlinear regression model. Specifically, given a neural network whose output $y$ depends only on a small subset of input $\boldsymbol{x}$, denoted by $\mathcal{S}^{\star}$, we prove that the LASSO estimator can stably reconstruct the neural network and identify $\mathcal{S}^{\star}$ when the number of samples scales logarithmically with the input dimension. This challenging regime has been well understood for linear models while barely studied for neural networks. Our theory lies in an extended Restricted Isometry Property (RIP)-based analysis framework for two-layer ReLU neural networks, which may be of independent interest to other LASSO or neural network settings. Based on the result, we advocate a neural network-based variable selection method. Experiments on simulated and real-world datasets show promising performance of the variable selection approach compared with existing techniques.
Pruning Deep Neural Networks from a Sparsity Perspective
Feb 11, 2023Abstract:In recent years, deep network pruning has attracted significant attention in order to enable the rapid deployment of AI into small devices with computation and memory constraints. Pruning is often achieved by dropping redundant weights, neurons, or layers of a deep network while attempting to retain a comparable test performance. Many deep pruning algorithms have been proposed with impressive empirical success. However, existing approaches lack a quantifiable measure to estimate the compressibility of a sub-network during each pruning iteration and thus may under-prune or over-prune the model. In this work, we propose PQ Index (PQI) to measure the potential compressibility of deep neural networks and use this to develop a Sparsity-informed Adaptive Pruning (SAP) algorithm. Our extensive experiments corroborate the hypothesis that for a generic pruning procedure, PQI decreases first when a large model is being effectively regularized and then increases when its compressibility reaches a limit that appears to correspond to the beginning of underfitting. Subsequently, PQI decreases again when the model collapse and significant deterioration in the performance of the model start to occur. Additionally, our experiments demonstrate that the proposed adaptive pruning algorithm with proper choice of hyper-parameters is superior to the iterative pruning algorithms such as the lottery ticket-based pruning methods, in terms of both compression efficiency and robustness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge