Dilshod Azizov
Profiling News Media for Factuality and Bias Using LLMs and the Fact-Checking Methodology of Human Experts
Jun 14, 2025Abstract:In an age characterized by the proliferation of mis- and disinformation online, it is critical to empower readers to understand the content they are reading. Important efforts in this direction rely on manual or automatic fact-checking, which can be challenging for emerging claims with limited information. Such scenarios can be handled by assessing the reliability and the political bias of the source of the claim, i.e., characterizing entire news outlets rather than individual claims or articles. This is an important but understudied research direction. While prior work has looked into linguistic and social contexts, we do not analyze individual articles or information in social media. Instead, we propose a novel methodology that emulates the criteria that professional fact-checkers use to assess the factuality and political bias of an entire outlet. Specifically, we design a variety of prompts based on these criteria and elicit responses from large language models (LLMs), which we aggregate to make predictions. In addition to demonstrating sizable improvements over strong baselines via extensive experiments with multiple LLMs, we provide an in-depth error analysis of the effect of media popularity and region on model performance. Further, we conduct an ablation study to highlight the key components of our dataset that contribute to these improvements. To facilitate future research, we released our dataset and code at https://github.com/mbzuai-nlp/llm-media-profiling.
Evolution of AI in Education: Agentic Workflows
Apr 25, 2025
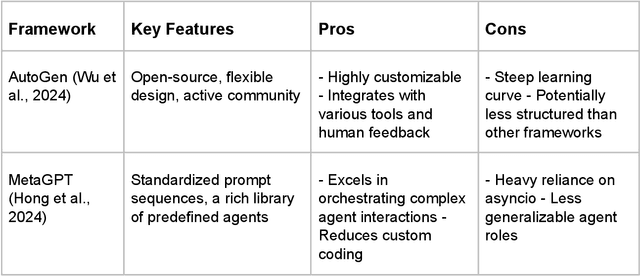
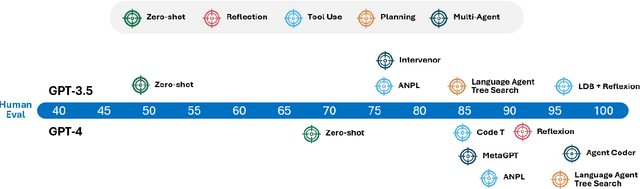
Abstract:Artificial intelligence (AI) has transformed various aspects of education, with large language models (LLMs) driving advancements in automated tutoring, assessment, and content generation. However, conventional LLMs are constrained by their reliance on static training data, limited adaptability, and lack of reasoning. To address these limitations and foster more sustainable technological practices, AI agents have emerged as a promising new avenue for educational innovation. In this review, we examine agentic workflows in education according to four major paradigms: reflection, planning, tool use, and multi-agent collaboration. We critically analyze the role of AI agents in education through these key design paradigms, exploring their advantages, applications, and challenges. To illustrate the practical potential of agentic systems, we present a proof-of-concept application: a multi-agent framework for automated essay scoring. Preliminary results suggest this agentic approach may offer improved consistency compared to stand-alone LLMs. Our findings highlight the transformative potential of AI agents in educational settings while underscoring the need for further research into their interpretability, trustworthiness, and sustainable impact on pedagogical impact.
CoDet-M4: Detecting Machine-Generated Code in Multi-Lingual, Multi-Generator and Multi-Domain Settings
Mar 17, 2025Abstract:Large language models (LLMs) have revolutionized code generation, automating programming with remarkable efficiency. However, these advancements challenge programming skills, ethics, and assessment integrity, making the detection of LLM-generated code essential for maintaining accountability and standards. While, there has been some research on this problem, it generally lacks domain coverage and robustness, and only covers a small number of programming languages. To this end, we propose a framework capable of distinguishing between human- and LLM-written code across multiple programming languages, code generators, and domains. We use a large-scale dataset from renowned platforms and LLM-based code generators, alongside applying rigorous data quality checks, feature engineering, and comparative analysis using evaluation of traditional machine learning models, pre-trained language models (PLMs), and LLMs for code detection. We perform an evaluation on out-of-domain scenarios, such as detecting the authorship and hybrid authorship of generated code and generalizing to unseen models, domains, and programming languages. Moreover, our extensive experiments show that our framework effectively distinguishes human- from LLM-written code and sets a new benchmark for this task.
A Decade of Deep Learning: A Survey on The Magnificent Seven
Dec 13, 2024Abstract:Deep learning has fundamentally reshaped the landscape of artificial intelligence over the past decade, enabling remarkable achievements across diverse domains. At the heart of these developments lie multi-layered neural network architectures that excel at automatic feature extraction, leading to significant improvements in machine learning tasks. To demystify these advances and offer accessible guidance, we present a comprehensive overview of the most influential deep learning algorithms selected through a broad-based survey of the field. Our discussion centers on pivotal architectures, including Residual Networks, Transformers, Generative Adversarial Networks, Variational Autoencoders, Graph Neural Networks, Contrastive Language-Image Pre-training, and Diffusion models. We detail their historical context, highlight their mathematical foundations and algorithmic principles, and examine subsequent variants, extensions, and practical considerations such as training methodologies, normalization techniques, and learning rate schedules. Beyond historical and technical insights, we also address their applications, challenges, and potential research directions. This survey aims to serve as a practical manual for both newcomers seeking an entry point into cutting-edge deep learning methods and experienced researchers transitioning into this rapidly evolving domain.
MGM: Global Understanding of Audience Overlap Graphs for Predicting the Factuality and the Bias of News Media
Dec 12, 2024



Abstract:In the current era of rapidly growing digital data, evaluating the political bias and factuality of news outlets has become more important for seeking reliable information online. In this work, we study the classification problem of profiling news media from the lens of political bias and factuality. Traditional profiling methods, such as Pre-trained Language Models (PLMs) and Graph Neural Networks (GNNs) have shown promising results, but they face notable challenges. PLMs focus solely on textual features, causing them to overlook the complex relationships between entities, while GNNs often struggle with media graphs containing disconnected components and insufficient labels. To address these limitations, we propose MediaGraphMind (MGM), an effective solution within a variational Expectation-Maximization (EM) framework. Instead of relying on limited neighboring nodes, MGM leverages features, structural patterns, and label information from globally similar nodes. Such a framework not only enables GNNs to capture long-range dependencies for learning expressive node representations but also enhances PLMs by integrating structural information and therefore improving the performance of both models. The extensive experiments demonstrate the effectiveness of the proposed framework and achieve new state-of-the-art results. Further, we share our repository1 which contains the dataset, code, and documentation
All Languages Matter: Evaluating LMMs on Culturally Diverse 100 Languages
Nov 25, 2024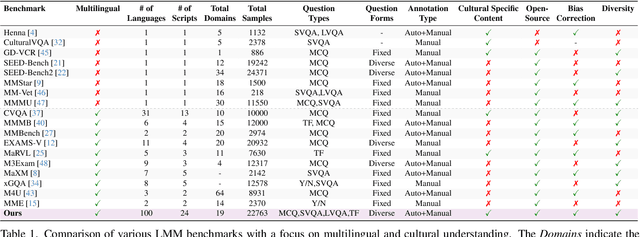
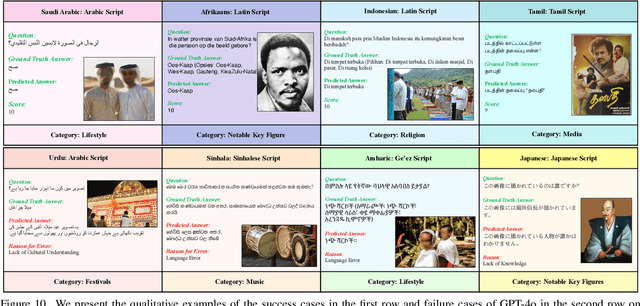
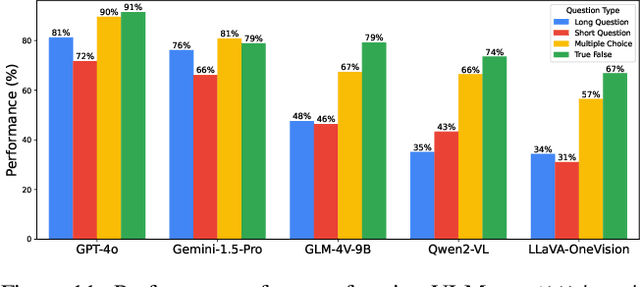
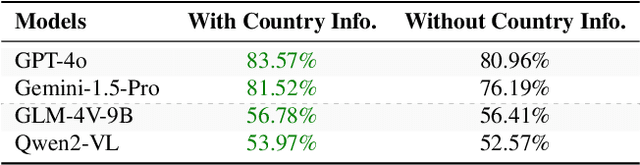
Abstract:Existing Large Multimodal Models (LMMs) generally focus on only a few regions and languages. As LMMs continue to improve, it is increasingly important to ensure they understand cultural contexts, respect local sensitivities, and support low-resource languages, all while effectively integrating corresponding visual cues. In pursuit of culturally diverse global multimodal models, our proposed All Languages Matter Benchmark (ALM-bench) represents the largest and most comprehensive effort to date for evaluating LMMs across 100 languages. ALM-bench challenges existing models by testing their ability to understand and reason about culturally diverse images paired with text in various languages, including many low-resource languages traditionally underrepresented in LMM research. The benchmark offers a robust and nuanced evaluation framework featuring various question formats, including true/false, multiple choice, and open-ended questions, which are further divided into short and long-answer categories. ALM-bench design ensures a comprehensive assessment of a model's ability to handle varied levels of difficulty in visual and linguistic reasoning. To capture the rich tapestry of global cultures, ALM-bench carefully curates content from 13 distinct cultural aspects, ranging from traditions and rituals to famous personalities and celebrations. Through this, ALM-bench not only provides a rigorous testing ground for state-of-the-art open and closed-source LMMs but also highlights the importance of cultural and linguistic inclusivity, encouraging the development of models that can serve diverse global populations effectively. Our benchmark is publicly available.
Contrastive Continual Learning with Importance Sampling and Prototype-Instance Relation Distillation
Mar 07, 2024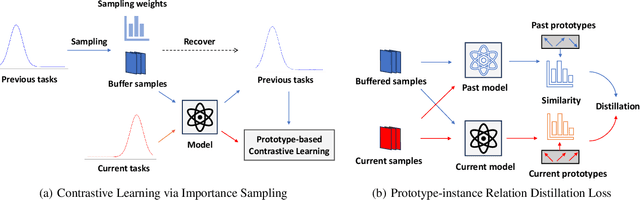
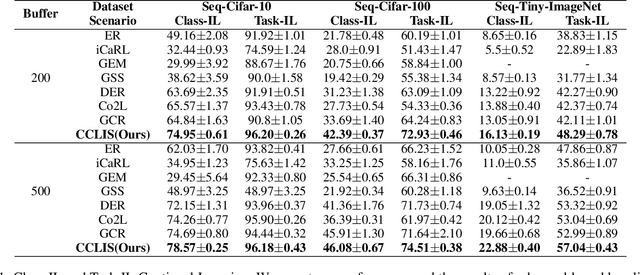
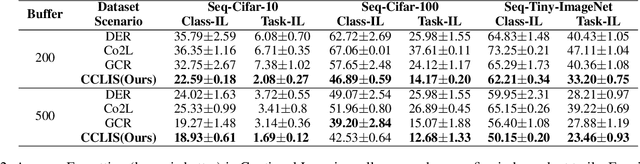
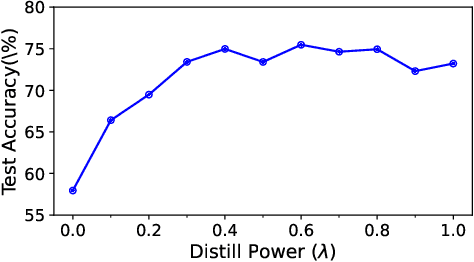
Abstract:Recently, because of the high-quality representations of contrastive learning methods, rehearsal-based contrastive continual learning has been proposed to explore how to continually learn transferable representation embeddings to avoid the catastrophic forgetting issue in traditional continual settings. Based on this framework, we propose Contrastive Continual Learning via Importance Sampling (CCLIS) to preserve knowledge by recovering previous data distributions with a new strategy for Replay Buffer Selection (RBS), which minimize estimated variance to save hard negative samples for representation learning with high quality. Furthermore, we present the Prototype-instance Relation Distillation (PRD) loss, a technique designed to maintain the relationship between prototypes and sample representations using a self-distillation process. Experiments on standard continual learning benchmarks reveal that our method notably outperforms existing baselines in terms of knowledge preservation and thereby effectively counteracts catastrophic forgetting in online contexts. The code is available at https://github.com/lijy373/CCLIS.
Computational Complexity of Sub-Linear Convergent Algorithms
Oct 05, 2022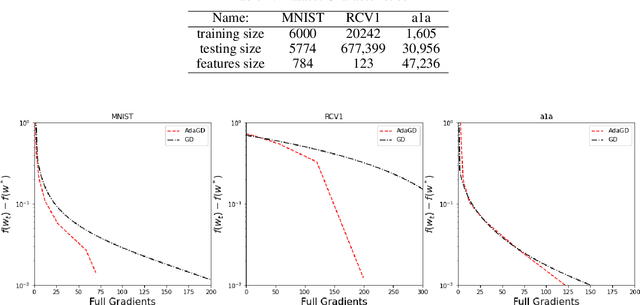

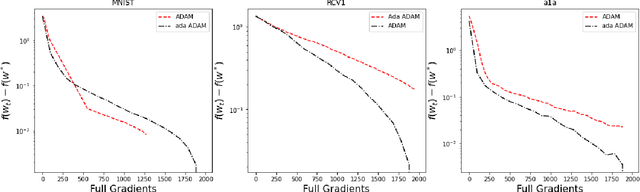
Abstract:Optimizing machine learning algorithms that are used to solve the objective function has been of great interest. Several approaches to optimize common algorithms, such as gradient descent and stochastic gradient descent, were explored. One of these approaches is reducing the gradient variance through adaptive sampling to solve large-scale optimization's empirical risk minimization (ERM) problems. In this paper, we will explore how starting with a small sample and then geometrically increasing it and using the solution of the previous sample ERM to compute the new ERM. This will solve ERM problems with first-order optimization algorithms of sublinear convergence but with lower computational complexity. This paper starts with theoretical proof of the approach, followed by two experiments comparing the gradient descent with the adaptive sampling of the gradient descent and ADAM with adaptive sampling ADAM on different datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge