Verification and Validation of a Vision-Based Landing System for Autonomous VTOL Air Taxis

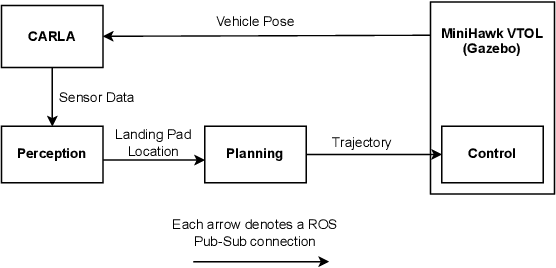
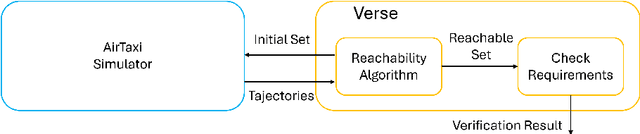
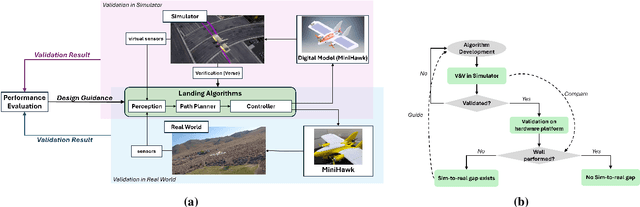
Autonomous air taxis are poised to revolutionize urban mass transportation, however, ensuring their safety and reliability remains an open challenge. Validating autonomy solutions on air taxis in the real world presents complexities, risks, and costs that further convolute this challenge. Verification and Validation (V&V) frameworks play a crucial role in the design and development of highly reliable systems by formally verifying safety properties and validating algorithm behavior across diverse operational scenarios. Advancements in high-fidelity simulators have significantly enhanced their capability to emulate real-world conditions, encouraging their use for validating autonomous air taxi solutions, especially during early development stages. This evolution underscores the growing importance of simulation environments, not only as complementary tools to real-world testing but as essential platforms for evaluating algorithms in a controlled, reproducible, and scalable manner. This work presents a V&V framework for a vision-based landing system for air taxis with vertical take-off and landing (VTOL) capabilities. Specifically, we use Verse, a tool for formal verification, to model and verify the safety of the system by obtaining and analyzing the reachable sets. To conduct this analysis, we utilize a photorealistic simulation environment. The simulation environment, built on Unreal Engine, provides realistic terrain, weather, and sensor characteristics to emulate real-world conditions with high fidelity. To validate the safety analysis results, we conduct extensive scenario-based testing to assess the reachability set and robustness of the landing algorithm in various conditions. This approach showcases the representativeness of high-fidelity simulators, offering an effective means to analyze and refine algorithms before real-world deployment.

CROPS: A Deployable Crop Management System Over All Possible State Availabilities

Exploring the optimal management strategy for nitrogen and irrigation has a significant impact on crop yield, economic profit, and the environment. To tackle this optimization challenge, this paper introduces a deployable \textbf{CR}op Management system \textbf{O}ver all \textbf{P}ossible \textbf{S}tate availabilities (CROPS). CROPS employs a language model (LM) as a reinforcement learning (RL) agent to explore optimal management strategies within the Decision Support System for Agrotechnology Transfer (DSSAT) crop simulations. A distinguishing feature of this system is that the states used for decision-making are partially observed through random masking. Consequently, the RL agent is tasked with two primary objectives: optimizing management policies and inferring masked states. This approach significantly enhances the RL agent's robustness and adaptability across various real-world agricultural scenarios. Extensive experiments on maize crops in Florida, USA, and Zaragoza, Spain, validate the effectiveness of CROPS. Not only did CROPS achieve State-of-the-Art (SOTA) results across various evaluation metrics such as production, profit, and sustainability, but the trained management policies are also immediately deployable in over of ten millions of real-world contexts. Furthermore, the pre-trained policies possess a noise resilience property, which enables them to minimize potential sensor biases, ensuring robustness and generalizability. Finally, unlike previous methods, the strength of CROPS lies in its unified and elegant structure, which eliminates the need for pre-defined states or multi-stage training. These advancements highlight the potential of CROPS in revolutionizing agricultural practices.

Resilient Estimator-based Control Barrier Functions for Dynamical Systems with Disturbances and Noise

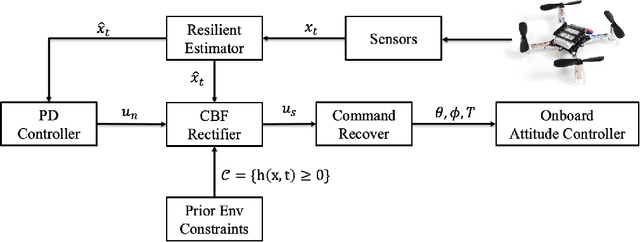
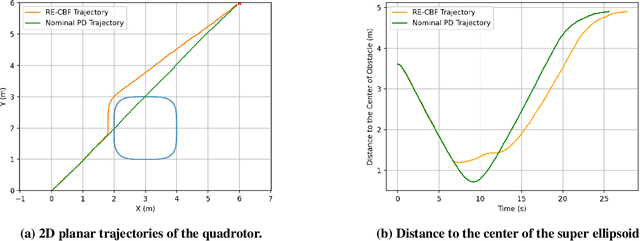
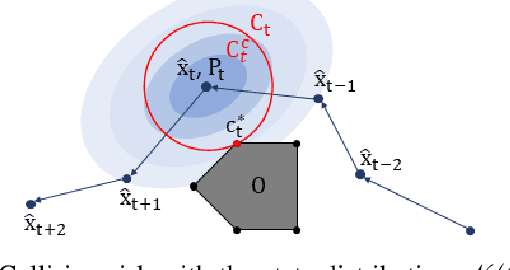
Control Barrier Function (CBF) is an emerging method that guarantees safety in path planning problems by generating a control command to ensure the forward invariance of a safety set. Most of the developments up to date assume availability of correct state measurements and absence of disturbances on the system. However, if the system incurs disturbances and is subject to noise, the CBF cannot guarantee safety due to the distorted state estimate. To improve the resilience and adaptability of the CBF, we propose a resilient estimator-based control barrier function (RE-CBF), which is based on a novel stochastic CBF optimization and resilient estimator, to guarantee the safety of systems with disturbances and noise in the path planning problems. The proposed algorithm uses the resilient estimation algorithm to estimate disturbances and counteract their effect using novel stochastic CBF optimization, providing safe control inputs for dynamical systems with disturbances and noise. To demonstrate the effectiveness of our algorithm in handling both noise and disturbances in dynamics and measurement, we design a quadrotor testing pipeline to simulate the proposed algorithm and then implement the algorithm on a real drone in our flying arena. Both simulations and real-world experiments show that the proposed method can guarantee safety for systems with disturbances and noise.

An Optimization-Based Planner with B-spline Parameterized Continuous-Time Reference Signals

For the cascaded planning and control modules implemented for robot navigation, the frequency gap between the planner and controller has received limited attention. In this study, we introduce a novel B-spline parameterized optimization-based planner (BSPOP) designed to address the frequency gap challenge with limited onboard computational power in robots. The proposed planner generates continuous-time control inputs for low-level controllers running at arbitrary frequencies to track. Furthermore, when considering the convex control action sets, BSPOP uses the convex hull property to automatically constrain the continuous-time control inputs within the convex set. Consequently, compared with the discrete-time optimization-based planners, BSPOP reduces the number of decision variables and inequality constraints, which improves computational efficiency as a byproduct. Simulation results demonstrate that our approach can achieve a comparable planning performance to the high-frequency baseline optimization-based planners while demanding less computational power. Both simulation and experiment results show that the proposed method performs better in planning compared with baseline planners in the same frequency.

RRT Guided Model Predictive Path Integral Method

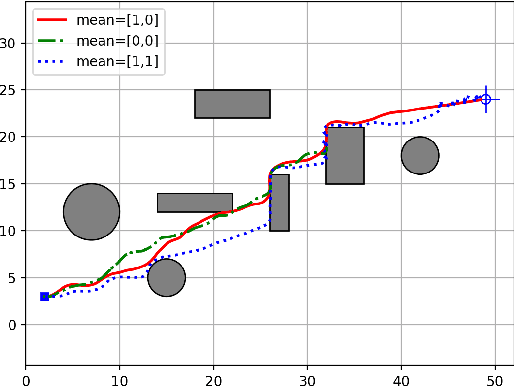
This work presents an optimal sampling-based method to solve the real-time motion planning problem in static and dynamic environments, exploiting the Rapid-exploring Random Trees (RRT) algorithm and the Model Predictive Path Integral (MPPI) algorithm. The RRT algorithm provides a nominal mean value of the random control distribution in the MPPI algorithm, resulting in satisfactory control performance in static and dynamic environments without a need for fine parameter tuning. We also discuss the importance of choosing the right mean of the MPPI algorithm, which balances exploration and optimality gap, given a fixed sample size. In particular, a sufficiently large mean is required to explore the state space enough, and a sufficiently small mean is required to guarantee that the samples reconstruct the optimal controls. The proposed methodology automates the procedure of choosing the right mean by incorporating the RRT algorithm. The simulations demonstrate that the proposed algorithm can solve the motion planning problem in real-time for static or dynamic environments.

Sampling Complexity of Path Integral Methods for Trajectory Optimization

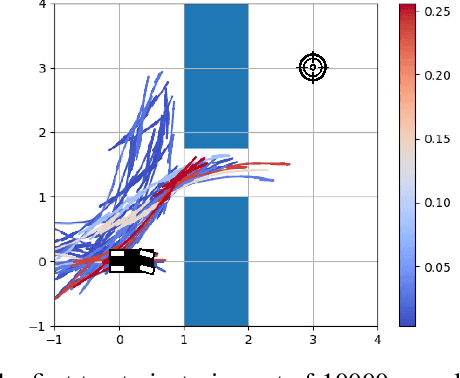
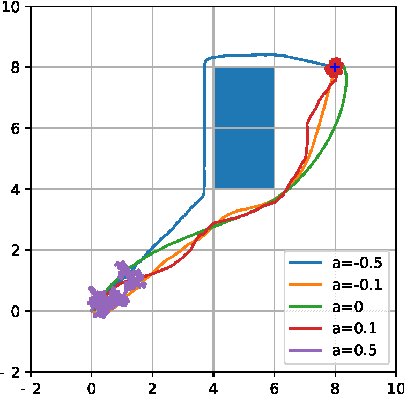
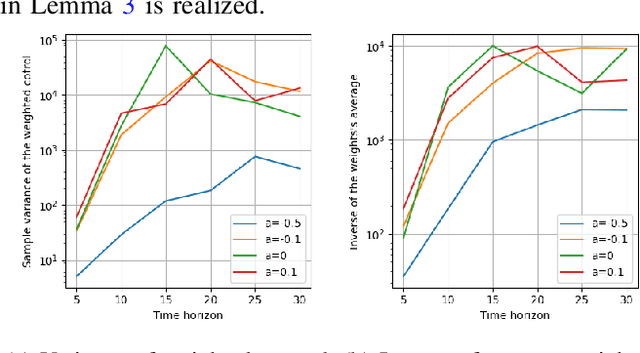
The use of random sampling in decision-making and control has become popular with the ease of access to graphic processing units that can generate and calculate multiple random trajectories for real-time robotic applications. In contrast to sequential optimization, the sampling-based method can take advantage of parallel computing to maintain constant control loop frequencies. Inspired by its wide applicability in robotic applications, we calculate a sampling complexity result applicable to general nonlinear systems considered in the path integral method, which is a sampling-based method. The result determines the required number of samples to satisfy the given error bounds of the estimated control signal from the optimal value with the predefined risk probability. The sampling complexity result shows that the variance of the estimated control value is upper-bounded in terms of the expectation of the cost. Then we apply the result to a linear time-varying dynamical system with quadratic cost and an indicator function cost to avoid constraint sets.