CoDe: Communication Delay-Tolerant Multi-Agent Collaboration via Dual Alignment of Intent and Timeliness

Communication has been widely employed to enhance multi-agent collaboration. Previous research has typically assumed delay-free communication, a strong assumption that is challenging to meet in practice. However, real-world agents suffer from channel delays, receiving messages sent at different time points, termed {\it{Asynchronous Communication}}, leading to cognitive biases and breakdowns in collaboration. This paper first defines two communication delay settings in MARL and emphasizes their harm to collaboration. To handle the above delays, this paper proposes a novel framework, Communication Delay-tolerant Multi-Agent Collaboration (CoDe). At first, CoDe learns an intent representation as messages through future action inference, reflecting the stable future behavioral trends of the agents. Then, CoDe devises a dual alignment mechanism of intent and timeliness to strengthen the fusion process of asynchronous messages. In this way, agents can extract the long-term intent of others, even from delayed messages, and selectively utilize the most recent messages that are relevant to their intent. Experimental results demonstrate that CoDe outperforms baseline algorithms in three MARL benchmarks without delay and exhibits robustness under fixed and time-varying delays.

MPCODER: Multi-user Personalized Code Generator with Explicit and Implicit Style Representation Learning

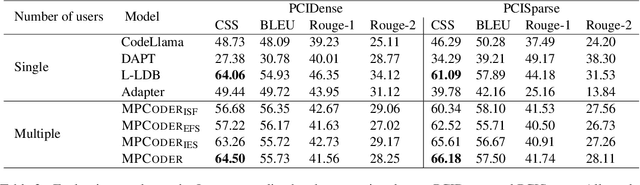
Large Language Models (LLMs) have demonstrated great potential for assisting developers in their daily development. However, most research focuses on generating correct code, how to use LLMs to generate personalized code has seldom been investigated. To bridge this gap, we proposed MPCoder (Multi-user Personalized Code Generator) to generate personalized code for multiple users. To better learn coding style features, we utilize explicit coding style residual learning to capture the syntax code style standards and implicit style learning to capture the semantic code style conventions. We train a multi-user style adapter to better differentiate the implicit feature representations of different users through contrastive learning, ultimately enabling personalized code generation for multiple users. We further propose a novel evaluation metric for estimating similarities between codes of different coding styles. The experimental results show the effectiveness of our approach for this novel task.

Improved Regret for Bandit Convex Optimization with Delayed Feedback

We investigate bandit convex optimization (BCO) with delayed feedback, where only the loss value of the action is revealed under an arbitrary delay. Previous studies have established a regret bound of $O(T^{3/4}+d^{1/3}T^{2/3})$ for this problem, where $d$ is the maximum delay, by simply feeding delayed loss values to the classical bandit gradient descent (BGD) algorithm. In this paper, we develop a novel algorithm to enhance the regret, which carefully exploits the delayed bandit feedback via a blocking update mechanism. Our analysis first reveals that the proposed algorithm can decouple the joint effect of the delays and bandit feedback on the regret, and improve the regret bound to $O(T^{3/4}+\sqrt{dT})$ for convex functions. Compared with the previous result, our regret matches the $O(T^{3/4})$ regret of BGD in the non-delayed setting for a larger amount of delay, i.e., $d=O(\sqrt{T})$, instead of $d=O(T^{1/4})$. Furthermore, we consider the case with strongly convex functions, and prove that the proposed algorithm can enjoy a better regret bound of $O(T^{2/3}\log^{1/3}T+d\log T)$. Finally, we show that in a special case with unconstrained action sets, it can be simply extended to achieve a regret bound of $O(\sqrt{T\log T}+d\log T)$ for strongly convex and smooth functions.

Improved Projection-free Online Continuous Submodular Maximization

We investigate the problem of online learning with monotone and continuous DR-submodular reward functions, which has received great attention recently. To efficiently handle this problem, especially in the case with complicated decision sets, previous studies have proposed an efficient projection-free algorithm called Mono-Frank-Wolfe (Mono-FW) using $O(T)$ gradient evaluations and linear optimization steps in total. However, it only attains a $(1-1/e)$-regret bound of $O(T^{4/5})$. In this paper, we propose an improved projection-free algorithm, namely POBGA, which reduces the regret bound to $O(T^{3/4})$ while keeping the same computational complexity as Mono-FW. Instead of modifying Mono-FW, our key idea is to make a novel combination of a projection-based algorithm called online boosting gradient ascent, an infeasible projection technique, and a blocking technique. Furthermore, we consider the decentralized setting and develop a variant of POBGA, which not only reduces the current best regret bound of efficient projection-free algorithms for this setting from $O(T^{4/5})$ to $O(T^{3/4})$, but also reduces the total communication complexity from $O(T)$ to $O(\sqrt{T})$.

Non-stationary Online Convex Optimization with Arbitrary Delays

Online convex optimization (OCO) with arbitrary delays, in which gradients or other information of functions could be arbitrarily delayed, has received increasing attention recently. Different from previous studies that focus on stationary environments, this paper investigates the delayed OCO in non-stationary environments, and aims to minimize the dynamic regret with respect to any sequence of comparators. To this end, we first propose a simple algorithm, namely DOGD, which performs a gradient descent step for each delayed gradient according to their arrival order. Despite its simplicity, our novel analysis shows that DOGD can attain an $O(\sqrt{dT}(P_T+1)$ dynamic regret bound in the worst case, where $d$ is the maximum delay, $T$ is the time horizon, and $P_T$ is the path length of comparators. More importantly, in case delays do not change the arrival order of gradients, it can automatically reduce the dynamic regret to $O(\sqrt{S}(1+P_T))$, where $S$ is the sum of delays. Furthermore, we develop an improved algorithm, which can reduce those dynamic regret bounds achieved by DOGD to $O(\sqrt{dT(P_T+1)})$ and $O(\sqrt{S(1+P_T)})$, respectively. The essential idea is to run multiple DOGD with different learning rates, and utilize a meta-algorithm to track the best one based on their delayed performance. Finally, we demonstrate that our improved algorithm is optimal in both cases by deriving a matching lower bound.

Claw U-Net: A Unet-based Network with Deep Feature Concatenation for Scleral Blood Vessel Segmentation

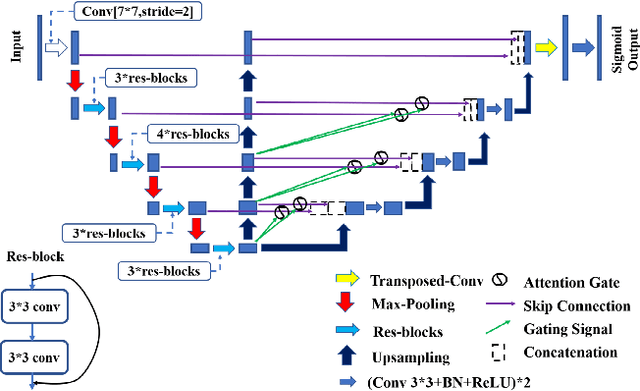
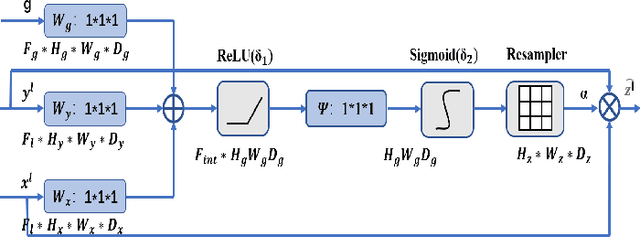
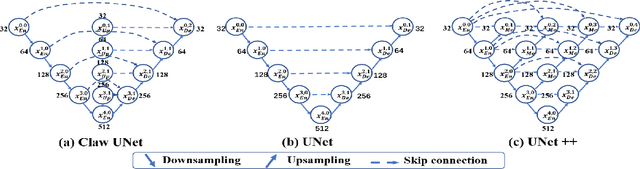
Sturge-Weber syndrome (SWS) is a vascular malformation disease, and it may cause blindness if the patient's condition is severe. Clinical results show that SWS can be divided into two types based on the characteristics of scleral blood vessels. Therefore, how to accurately segment scleral blood vessels has become a significant problem in computer-aided diagnosis. In this research, we propose to continuously upsample the bottom layer's feature maps to preserve image details, and design a novel Claw UNet based on UNet for scleral blood vessel segmentation. Specifically, the residual structure is used to increase the number of network layers in the feature extraction stage to learn deeper features. In the decoding stage, by fusing the features of the encoding, upsampling, and decoding parts, Claw UNet can achieve effective segmentation in the fine-grained regions of scleral blood vessels. To effectively extract small blood vessels, we use the attention mechanism to calculate the attention coefficient of each position in images. Claw UNet outperforms other UNet-based networks on scleral blood vessel image dataset.