CoDe: Communication Delay-Tolerant Multi-Agent Collaboration via Dual Alignment of Intent and Timeliness

Communication has been widely employed to enhance multi-agent collaboration. Previous research has typically assumed delay-free communication, a strong assumption that is challenging to meet in practice. However, real-world agents suffer from channel delays, receiving messages sent at different time points, termed {\it{Asynchronous Communication}}, leading to cognitive biases and breakdowns in collaboration. This paper first defines two communication delay settings in MARL and emphasizes their harm to collaboration. To handle the above delays, this paper proposes a novel framework, Communication Delay-tolerant Multi-Agent Collaboration (CoDe). At first, CoDe learns an intent representation as messages through future action inference, reflecting the stable future behavioral trends of the agents. Then, CoDe devises a dual alignment mechanism of intent and timeliness to strengthen the fusion process of asynchronous messages. In this way, agents can extract the long-term intent of others, even from delayed messages, and selectively utilize the most recent messages that are relevant to their intent. Experimental results demonstrate that CoDe outperforms baseline algorithms in three MARL benchmarks without delay and exhibits robustness under fixed and time-varying delays.

Improving Global Parameter-sharing in Physically Heterogeneous Multi-agent Reinforcement Learning with Unified Action Space

In a multi-agent system (MAS), action semantics indicates the different influences of agents' actions toward other entities, and can be used to divide agents into groups in a physically heterogeneous MAS. Previous multi-agent reinforcement learning (MARL) algorithms apply global parameter-sharing across different types of heterogeneous agents without careful discrimination of different action semantics. This common implementation decreases the cooperation and coordination between agents in complex situations. However, fully independent agent parameters dramatically increase the computational cost and training difficulty. In order to benefit from the usage of different action semantics while also maintaining a proper parameter-sharing structure, we introduce the Unified Action Space (UAS) to fulfill the requirement. The UAS is the union set of all agent actions with different semantics. All agents first calculate their unified representation in the UAS, and then generate their heterogeneous action policies using different available-action-masks. To further improve the training of extra UAS parameters, we introduce a Cross-Group Inverse (CGI) loss to predict other groups' agent policies with the trajectory information. As a universal method for solving the physically heterogeneous MARL problem, we implement the UAS adding to both value-based and policy-based MARL algorithms, and propose two practical algorithms: U-QMIX and U-MAPPO. Experimental results in the SMAC environment prove the effectiveness of both U-QMIX and U-MAPPO compared with several state-of-the-art MARL methods.

GHQ: Grouped Hybrid Q Learning for Heterogeneous Cooperative Multi-agent Reinforcement Learning

Previous deep multi-agent reinforcement learning (MARL) algorithms have achieved impressive results, typically in homogeneous scenarios. However, heterogeneous scenarios are also very common and usually harder to solve. In this paper, we mainly discuss cooperative heterogeneous MARL problems in Starcraft Multi-Agent Challenges (SMAC) environment. We firstly define and describe the heterogeneous problems in SMAC. In order to comprehensively reveal and study the problem, we make new maps added to the original SMAC maps. We find that baseline algorithms fail to perform well in those heterogeneous maps. To address this issue, we propose the Grouped Individual-Global-Max Consistency (GIGM) and a novel MARL algorithm, Grouped Hybrid Q Learning (GHQ). GHQ separates agents into several groups and keeps individual parameters for each group, along with a novel hybrid structure for factorization. To enhance coordination between groups, we maximize the Inter-group Mutual Information (IGMI) between groups' trajectories. Experiments on original and new heterogeneous maps show the fabulous performance of GHQ compared to other state-of-the-art algorithms.

Conservative Distributional Reinforcement Learning with Safety Constraints

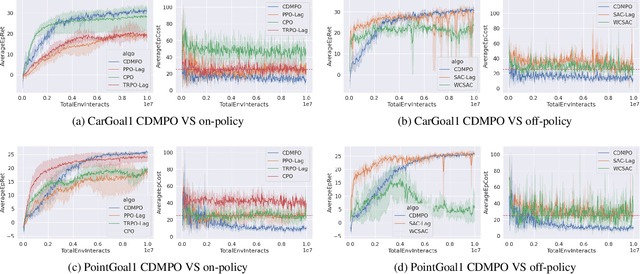
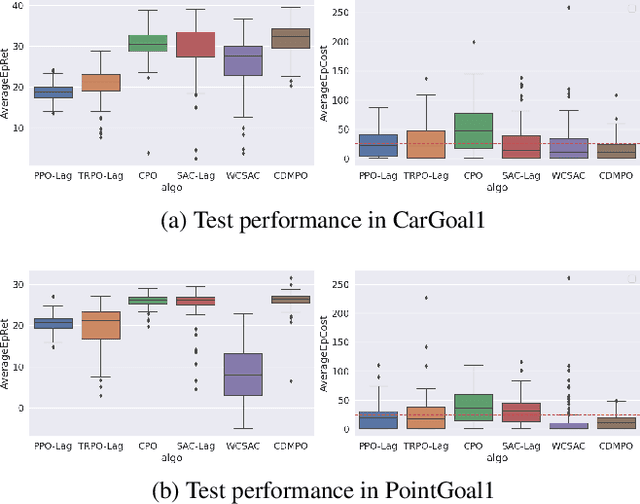
Safety exploration can be regarded as a constrained Markov decision problem where the expected long-term cost is constrained. Previous off-policy algorithms convert the constrained optimization problem into the corresponding unconstrained dual problem by introducing the Lagrangian relaxation technique. However, the cost function of the above algorithms provides inaccurate estimations and causes the instability of the Lagrange multiplier learning. In this paper, we present a novel off-policy reinforcement learning algorithm called Conservative Distributional Maximum a Posteriori Policy Optimization (CDMPO). At first, to accurately judge whether the current situation satisfies the constraints, CDMPO adapts distributional reinforcement learning method to estimate the Q-function and C-function. Then, CDMPO uses a conservative value function loss to reduce the number of violations of constraints during the exploration process. In addition, we utilize Weighted Average Proportional Integral Derivative (WAPID) to update the Lagrange multiplier stably. Empirical results show that the proposed method has fewer violations of constraints in the early exploration process. The final test results also illustrate that our method has better risk control.

$l_1$-regularized Outlier Isolation and Regression

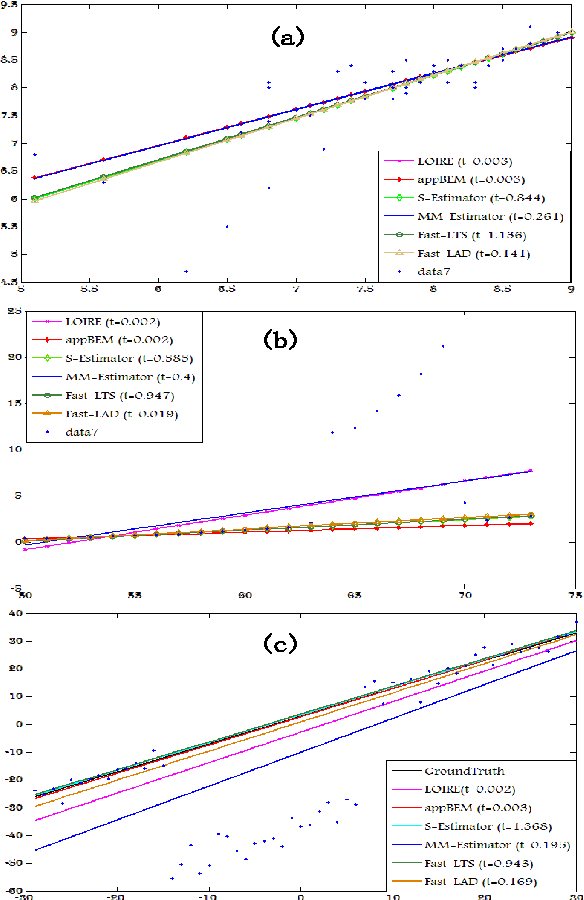
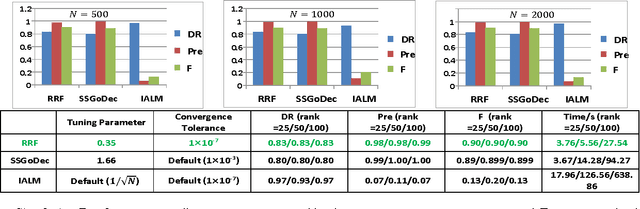
This paper proposed a new regression model called $l_1$-regularized outlier isolation and regression (LOIRE) and a fast algorithm based on block coordinate descent to solve this model. Besides, assuming outliers are gross errors following a Bernoulli process, this paper also presented a Bernoulli estimate model which, in theory, should be very accurate and robust due to its complete elimination of affections caused by outliers. Though this Bernoulli estimate is hard to solve, it could be approximately achieved through a process which takes LOIRE as an important intermediate step. As a result, the approximate Bernoulli estimate is a good combination of Bernoulli estimate's accuracy and LOIRE regression's efficiency with several simulations conducted to strongly verify this point. Moreover, LOIRE can be further extended to realize robust rank factorization which is powerful in recovering low-rank component from massive corruptions. Extensive experimental results showed that the proposed method outperforms state-of-the-art methods like RPCA and GoDec in the aspect of computation speed with a competitive performance.