$l_1$-regularized Outlier Isolation and Regression
Paper and Code
Nov 20, 2014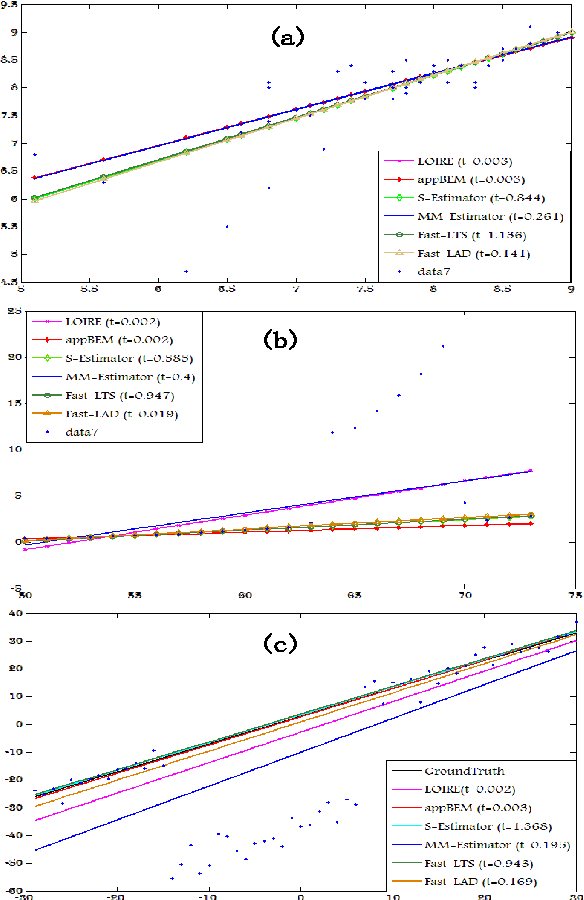
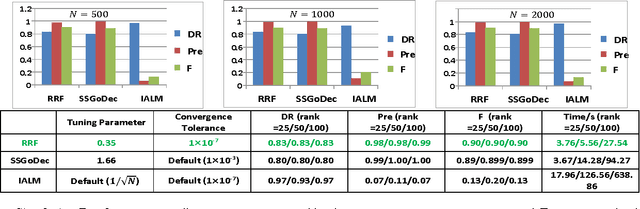

This paper proposed a new regression model called $l_1$-regularized outlier isolation and regression (LOIRE) and a fast algorithm based on block coordinate descent to solve this model. Besides, assuming outliers are gross errors following a Bernoulli process, this paper also presented a Bernoulli estimate model which, in theory, should be very accurate and robust due to its complete elimination of affections caused by outliers. Though this Bernoulli estimate is hard to solve, it could be approximately achieved through a process which takes LOIRE as an important intermediate step. As a result, the approximate Bernoulli estimate is a good combination of Bernoulli estimate's accuracy and LOIRE regression's efficiency with several simulations conducted to strongly verify this point. Moreover, LOIRE can be further extended to realize robust rank factorization which is powerful in recovering low-rank component from massive corruptions. Extensive experimental results showed that the proposed method outperforms state-of-the-art methods like RPCA and GoDec in the aspect of computation speed with a competitive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge