SMRD: SURE-based Robust MRI Reconstruction with Diffusion Models

Diffusion models have recently gained popularity for accelerated MRI reconstruction due to their high sample quality. They can effectively serve as rich data priors while incorporating the forward model flexibly at inference time, and they have been shown to be more robust than unrolled methods under distribution shifts. However, diffusion models require careful tuning of inference hyperparameters on a validation set and are still sensitive to distribution shifts during testing. To address these challenges, we introduce SURE-based MRI Reconstruction with Diffusion models (SMRD), a method that performs test-time hyperparameter tuning to enhance robustness during testing. SMRD uses Stein's Unbiased Risk Estimator (SURE) to estimate the mean squared error of the reconstruction during testing. SURE is then used to automatically tune the inference hyperparameters and to set an early stopping criterion without the need for validation tuning. To the best of our knowledge, SMRD is the first to incorporate SURE into the sampling stage of diffusion models for automatic hyperparameter selection. SMRD outperforms diffusion model baselines on various measurement noise levels, acceleration factors, and anatomies, achieving a PSNR improvement of up to 6 dB under measurement noise. The code is publicly available at https://github.com/NVlabs/SMRD .

Coil Sketching for computationally-efficient MR iterative reconstruction

Purpose: Parallel imaging and compressed sensing reconstructions of large MRI datasets often have a prohibitive computational cost that bottlenecks clinical deployment, especially for 3D non-Cartesian acquisitions. One common approach is to reduce the number of coil channels actively used during reconstruction as in coil compression. While effective for Cartesian imaging, coil compression inherently loses signal energy, producing shading artifacts that compromise image quality for 3D non-Cartesian imaging. We propose coil sketching, a general and versatile method for computationally-efficient iterative MR image reconstruction. Theory and Methods: We based our method on randomized sketching algorithms, a type of large-scale optimization algorithms well established in the fields of machine learning and big data analysis. We adapt the sketching theory to the MRI reconstruction problem via a structured sketching matrix that, similar to coil compression, reduces the number of coils concurrently used during reconstruction, but unlike coil compression, is able to leverage energy from all coils. Results: First, we performed ablation experiments to validate the sketching matrix design on both Cartesian and non-Cartesian datasets. The resulting design yielded both improved computational efficiency and preserved signal-to-noise ratio (SNR) as measured by the inverse g-factor. Then, we verified the efficacy of our approach on high-dimensional non-Cartesian 3D cones datasets, where coil sketching yielded up to three-fold faster reconstructions with equivalent image quality. Conclusion: Coil sketching is a general and versatile reconstruction framework for computationally fast and memory-efficient reconstruction.

Scale-Agnostic Super-Resolution in MRI using Feature-Based Coordinate Networks

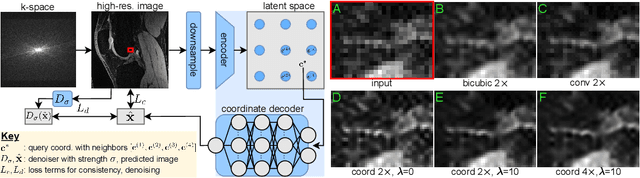
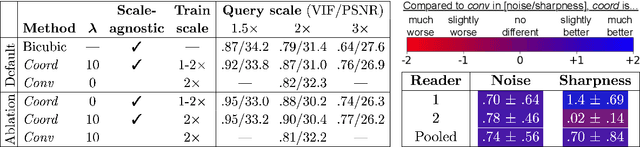
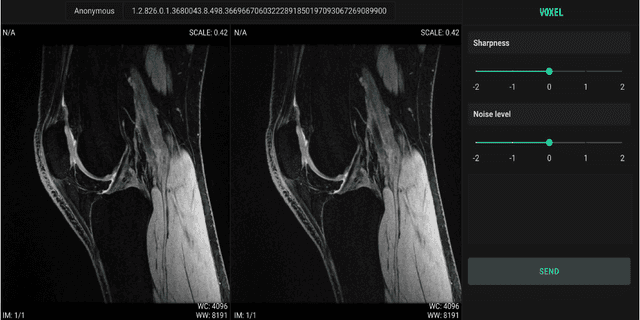
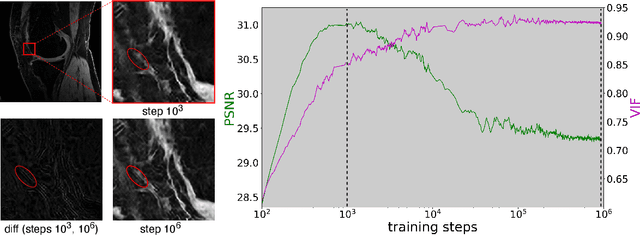
We propose using a coordinate network decoder for the task of super-resolution in MRI. The continuous signal representation of coordinate networks enables this approach to be scale-agnostic, i.e. one can train over a continuous range of scales and subsequently query at arbitrary resolutions. Due to the difficulty of performing super-resolution on inherently noisy data, we analyze network behavior under multiple denoising strategies. Lastly we compare this method to a standard convolutional decoder using both quantitative metrics and a radiologist study implemented in Voxel, our newly developed tool for web-based evaluation of medical images.

ThinkSum: Probabilistic reasoning over sets using large language models

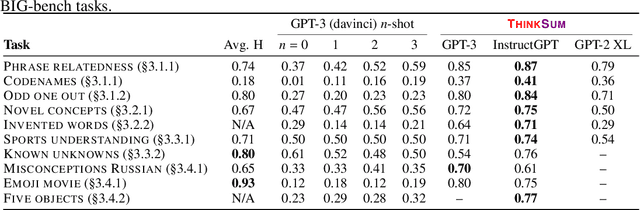
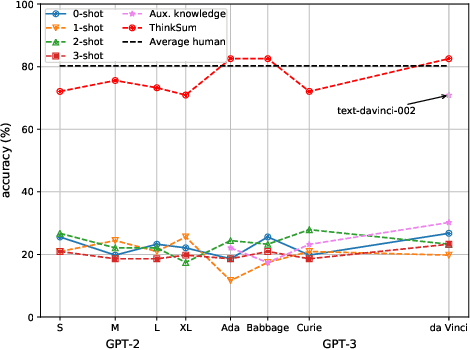
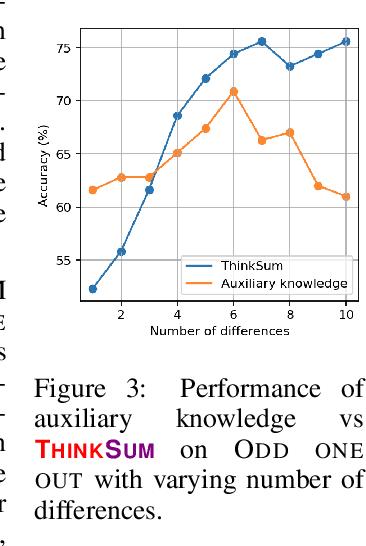
Large language models (LLMs) have a substantial capacity for high-level analogical reasoning: reproducing patterns in linear text that occur in their training data (zero-shot evaluation) or in the provided context (few-shot in-context learning). However, recent studies show that even the largest LLMs fail in scenarios that require reasoning over multiple objects or facts or making sequences of logical deductions. We propose a two-stage probabilistic inference paradigm, ThinkSum, that reasons over sets of objects or facts in a structured manner. In the first stage (Think -- 'fast' retrieval of associations), a LLM is queried in parallel over a set of phrases extracted from the prompt or an auxiliary model call. In the second stage (Sum -- 'slow' probabilistic inference or reasoning), the results of these queries are aggregated to make the final prediction. We demonstrate the advantages of ThinkSum on the BIG-bench suite of evaluation tasks, achieving improvements over the state of the art using GPT-family models on ten difficult tasks, often with far smaller model variants. We compare and contrast ThinkSum with other proposed modifications to direct prompting of LLMs, such as variants of chain-of-thought prompting. We argue that because the probabilistic inference in ThinkSum is performed outside of calls to the LLM, ThinkSum is less sensitive to prompt design, yields more interpretable predictions, and can be flexibly combined with latent variable models to extract structured knowledge from LLMs.

GLEAM: Greedy Learning for Large-Scale Accelerated MRI Reconstruction

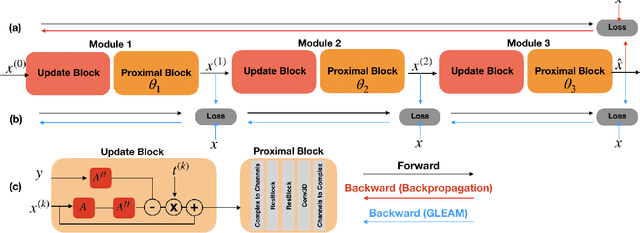
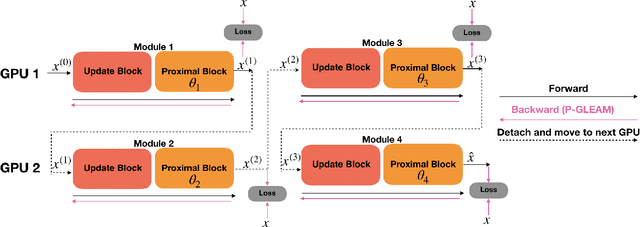
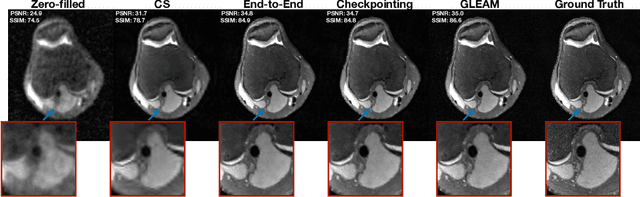
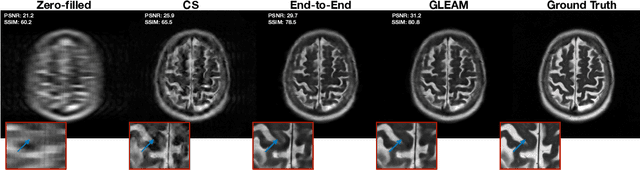
Unrolled neural networks have recently achieved state-of-the-art accelerated MRI reconstruction. These networks unroll iterative optimization algorithms by alternating between physics-based consistency and neural-network based regularization. However, they require several iterations of a large neural network to handle high-dimensional imaging tasks such as 3D MRI. This limits traditional training algorithms based on backpropagation due to prohibitively large memory and compute requirements for calculating gradients and storing intermediate activations. To address this challenge, we propose Greedy LEarning for Accelerated MRI (GLEAM) reconstruction, an efficient training strategy for high-dimensional imaging settings. GLEAM splits the end-to-end network into decoupled network modules. Each module is optimized in a greedy manner with decoupled gradient updates, reducing the memory footprint during training. We show that the decoupled gradient updates can be performed in parallel on multiple graphical processing units (GPUs) to further reduce training time. We present experiments with 2D and 3D datasets including multi-coil knee, brain, and dynamic cardiac cine MRI. We observe that: i) GLEAM generalizes as well as state-of-the-art memory-efficient baselines such as gradient checkpointing and invertible networks with the same memory footprint, but with 1.3x faster training; ii) for the same memory footprint, GLEAM yields 1.1dB PSNR gain in 2D and 1.8 dB in 3D over end-to-end baselines.

Unraveling Attention via Convex Duality: Analysis and Interpretations of Vision Transformers

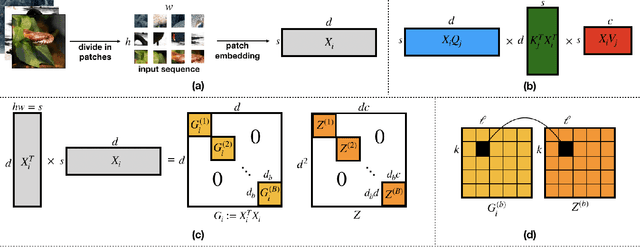
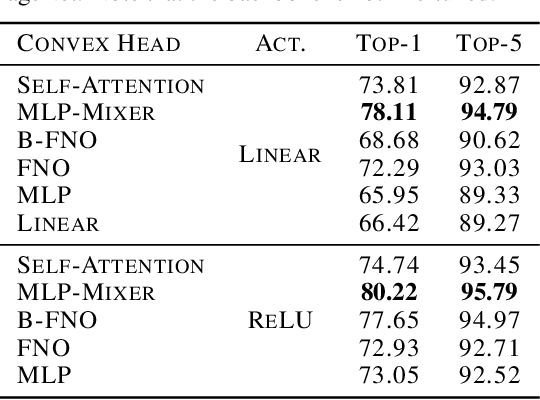
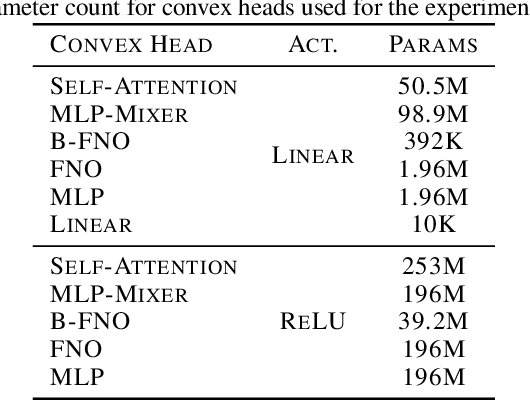
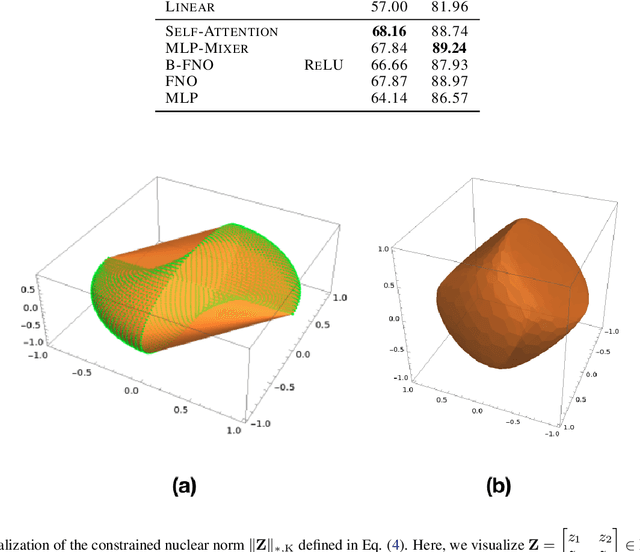
Vision transformers using self-attention or its proposed alternatives have demonstrated promising results in many image related tasks. However, the underpinning inductive bias of attention is not well understood. To address this issue, this paper analyzes attention through the lens of convex duality. For the non-linear dot-product self-attention, and alternative mechanisms such as MLP-mixer and Fourier Neural Operator (FNO), we derive equivalent finite-dimensional convex problems that are interpretable and solvable to global optimality. The convex programs lead to {\it block nuclear-norm regularization} that promotes low rank in the latent feature and token dimensions. In particular, we show how self-attention networks implicitly clusters the tokens, based on their latent similarity. We conduct experiments for transferring a pre-trained transformer backbone for CIFAR-100 classification by fine-tuning a variety of convex attention heads. The results indicate the merits of the bias induced by attention compared with the existing MLP or linear heads.

Hidden Convexity of Wasserstein GANs: Interpretable Generative Models with Closed-Form Solutions

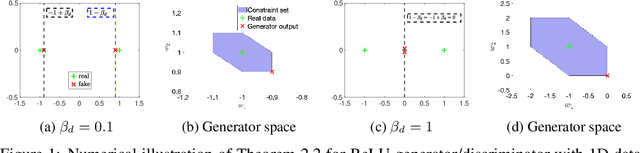
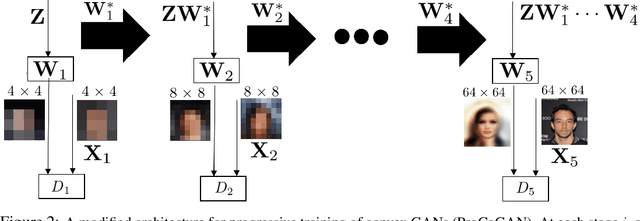
Generative Adversarial Networks (GANs) are commonly used for modeling complex distributions of data. Both the generators and discriminators of GANs are often modeled by neural networks, posing a non-transparent optimization problem which is non-convex and non-concave over the generator and discriminator, respectively. Such networks are often heuristically optimized with gradient descent-ascent (GDA), but it is unclear whether the optimization problem contains any saddle points, or whether heuristic methods can find them in practice. In this work, we analyze the training of Wasserstein GANs with two-layer neural network discriminators through the lens of convex duality, and for a variety of generators expose the conditions under which Wasserstein GANs can be solved exactly with convex optimization approaches, or can be represented as convex-concave games. Using this convex duality interpretation, we further demonstrate the impact of different activation functions of the discriminator. Our observations are verified with numerical results demonstrating the power of the convex interpretation, with applications in progressive training of convex architectures corresponding to linear generators and quadratic-activation discriminators for CelebA image generation. The code for our experiments is available at https://github.com/ardasahiner/ProCoGAN.

Demystifying Batch Normalization in ReLU Networks: Equivalent Convex Optimization Models and Implicit Regularization

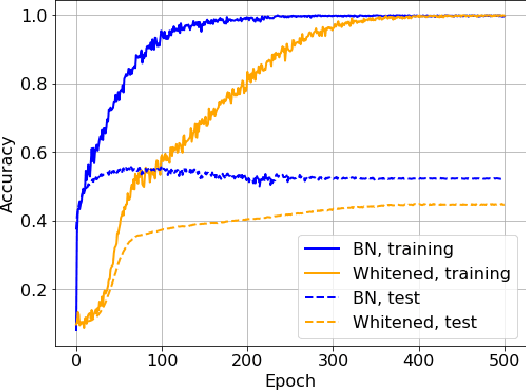
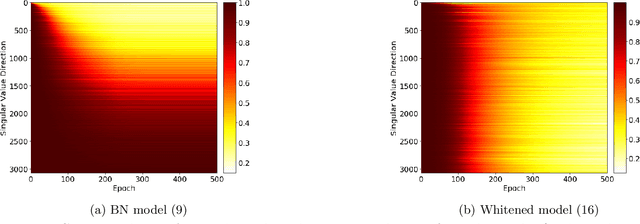
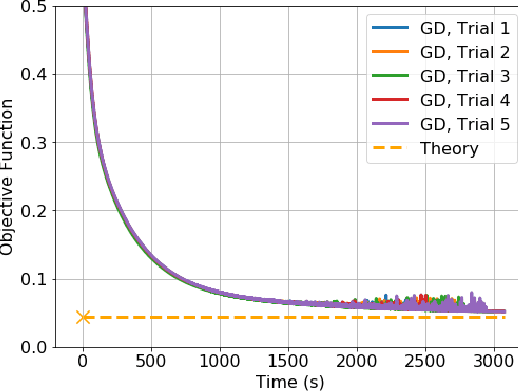
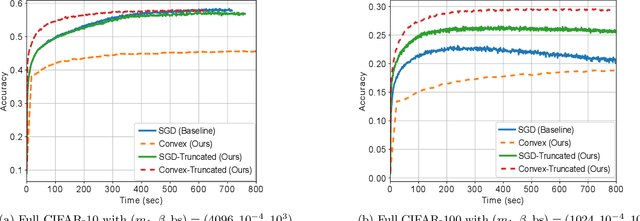
Batch Normalization (BN) is a commonly used technique to accelerate and stabilize training of deep neural networks. Despite its empirical success, a full theoretical understanding of BN is yet to be developed. In this work, we analyze BN through the lens of convex optimization. We introduce an analytic framework based on convex duality to obtain exact convex representations of weight-decay regularized ReLU networks with BN, which can be trained in polynomial-time. Our analyses also show that optimal layer weights can be obtained as simple closed-form formulas in the high-dimensional and/or overparameterized regimes. Furthermore, we find that Gradient Descent provides an algorithmic bias effect on the standard non-convex BN network, and we design an approach to explicitly encode this implicit regularization into the convex objective. Experiments with CIFAR image classification highlight the effectiveness of this explicit regularization for mimicking and substantially improving the performance of standard BN networks.

Convex Regularization Behind Neural Reconstruction

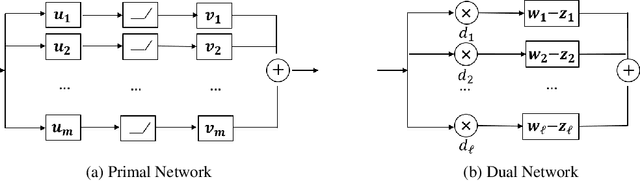
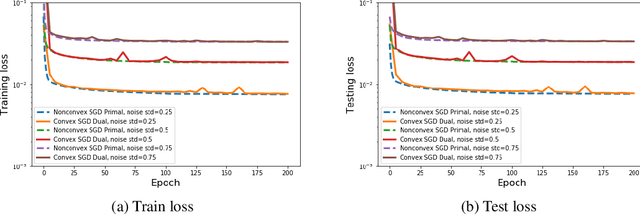
Neural networks have shown tremendous potential for reconstructing high-resolution images in inverse problems. The non-convex and opaque nature of neural networks, however, hinders their utility in sensitive applications such as medical imaging. To cope with this challenge, this paper advocates a convex duality framework that makes a two-layer fully-convolutional ReLU denoising network amenable to convex optimization. The convex dual network not only offers the optimum training with convex solvers, but also facilitates interpreting training and prediction. In particular, it implies training neural networks with weight decay regularization induces path sparsity while the prediction is piecewise linear filtering. A range of experiments with MNIST and fastMRI datasets confirm the efficacy of the dual network optimization problem.