Burak Bartan
KForge: Program Synthesis for Diverse AI Hardware Accelerators
Nov 17, 2025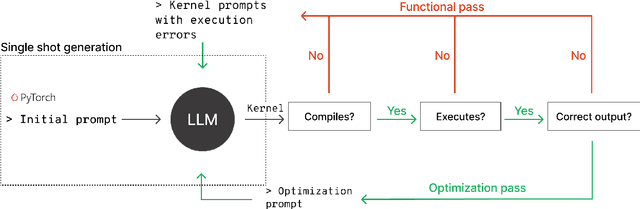

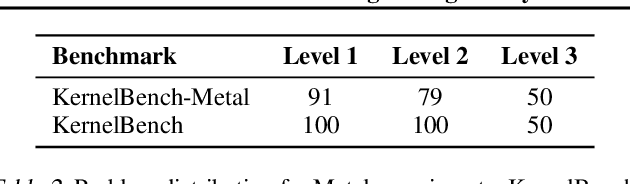
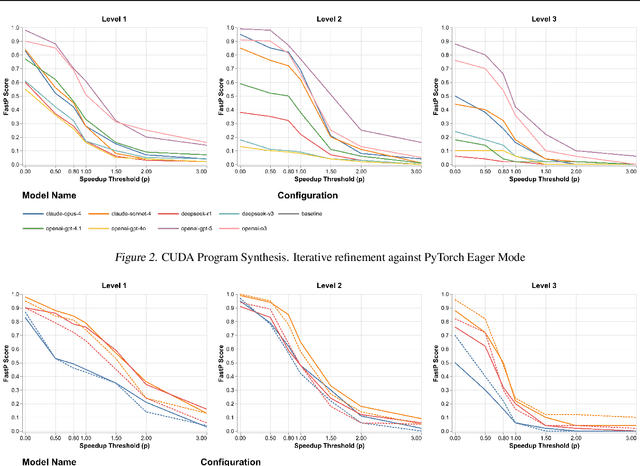
Abstract:GPU kernels are critical for ML performance but difficult to optimize across diverse accelerators. We present KForge, a platform-agnostic framework built on two collaborative LLM-based agents: a generation agent that produces and iteratively refines programs through compilation and correctness feedback, and a performance analysis agent that interprets profiling data to guide optimization. This agent-based architecture requires only a single-shot example to target new platforms. We make three key contributions: (1) introducing an iterative refinement system where the generation agent and performance analysis agent collaborate through functional and optimization passes, interpreting diverse profiling data (from programmatic APIs to GUI-based tools) to generate actionable recommendations that guide program synthesis for arbitrary accelerators; (2) demonstrating that the generation agent effectively leverages cross-platform knowledge transfer, where a reference implementation from one architecture substantially improves generation quality for different hardware targets; and (3) validating the platform-agnostic nature of our approach by demonstrating effective program synthesis across fundamentally different parallel computing platforms: NVIDIA CUDA and Apple Metal.
Randomized Polar Codes for Anytime Distributed Machine Learning
Sep 01, 2023



Abstract:We present a novel distributed computing framework that is robust to slow compute nodes, and is capable of both approximate and exact computation of linear operations. The proposed mechanism integrates the concepts of randomized sketching and polar codes in the context of coded computation. We propose a sequential decoding algorithm designed to handle real valued data while maintaining low computational complexity for recovery. Additionally, we provide an anytime estimator that can generate provably accurate estimates even when the set of available node outputs is not decodable. We demonstrate the potential applications of this framework in various contexts, such as large-scale matrix multiplication and black-box optimization. We present the implementation of these methods on a serverless cloud computing system and provide numerical results to demonstrate their scalability in practice, including ImageNet scale computations.
Moccasin: Efficient Tensor Rematerialization for Neural Networks
Apr 27, 2023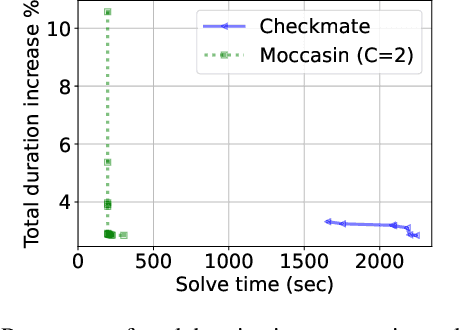

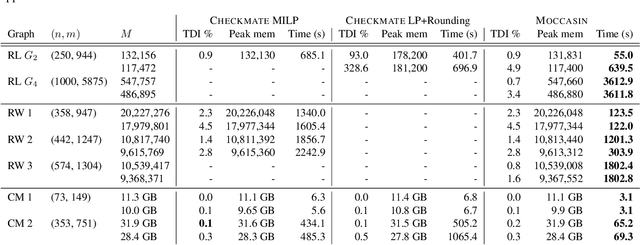
Abstract:The deployment and training of neural networks on edge computing devices pose many challenges. The low memory nature of edge devices is often one of the biggest limiting factors encountered in the deployment of large neural network models. Tensor rematerialization or recompute is a way to address high memory requirements for neural network training and inference. In this paper we consider the problem of execution time minimization of compute graphs subject to a memory budget. In particular, we develop a new constraint programming formulation called \textsc{Moccasin} with only $O(n)$ integer variables, where $n$ is the number of nodes in the compute graph. This is a significant improvement over the works in the recent literature that propose formulations with $O(n^2)$ Boolean variables. We present numerical studies that show that our approach is up to an order of magnitude faster than recent work especially for large-scale graphs.
Distributed Sketching for Randomized Optimization: Exact Characterization, Concentration and Lower Bounds
Mar 18, 2022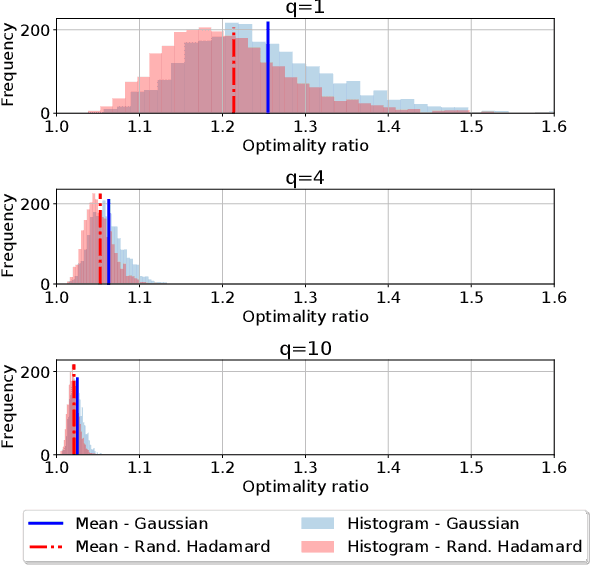
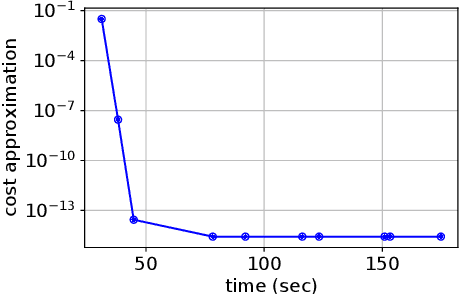
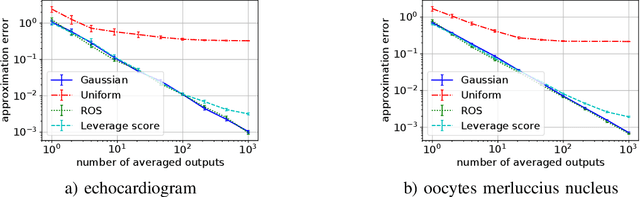
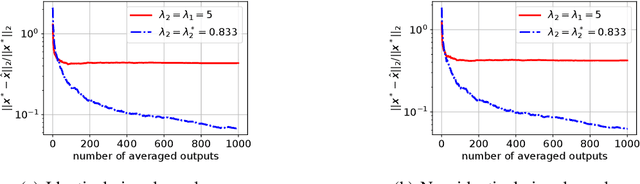
Abstract:We consider distributed optimization methods for problems where forming the Hessian is computationally challenging and communication is a significant bottleneck. We leverage randomized sketches for reducing the problem dimensions as well as preserving privacy and improving straggler resilience in asynchronous distributed systems. We derive novel approximation guarantees for classical sketching methods and establish tight concentration results that serve as both upper and lower bounds on the error. We then extend our analysis to the accuracy of parameter averaging for distributed sketches. Furthermore, we develop unbiased parameter averaging methods for randomized second order optimization for regularized problems that employ sketching of the Hessian. Existing works do not take the bias of the estimators into consideration, which limits their application to massively parallel computation. We provide closed-form formulas for regularization parameters and step sizes that provably minimize the bias for sketched Newton directions. Additionally, we demonstrate the implications of our theoretical findings via large scale experiments on a serverless cloud computing platform.
Hidden Convexity of Wasserstein GANs: Interpretable Generative Models with Closed-Form Solutions
Jul 12, 2021
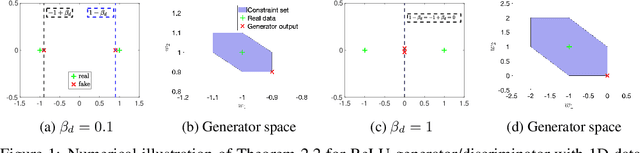
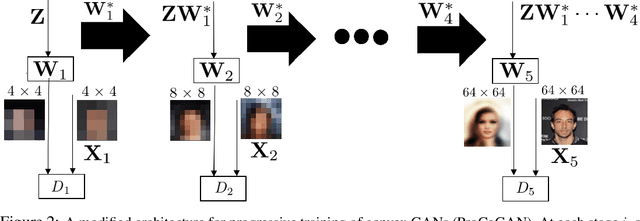

Abstract:Generative Adversarial Networks (GANs) are commonly used for modeling complex distributions of data. Both the generators and discriminators of GANs are often modeled by neural networks, posing a non-transparent optimization problem which is non-convex and non-concave over the generator and discriminator, respectively. Such networks are often heuristically optimized with gradient descent-ascent (GDA), but it is unclear whether the optimization problem contains any saddle points, or whether heuristic methods can find them in practice. In this work, we analyze the training of Wasserstein GANs with two-layer neural network discriminators through the lens of convex duality, and for a variety of generators expose the conditions under which Wasserstein GANs can be solved exactly with convex optimization approaches, or can be represented as convex-concave games. Using this convex duality interpretation, we further demonstrate the impact of different activation functions of the discriminator. Our observations are verified with numerical results demonstrating the power of the convex interpretation, with applications in progressive training of convex architectures corresponding to linear generators and quadratic-activation discriminators for CelebA image generation. The code for our experiments is available at https://github.com/ardasahiner/ProCoGAN.
Training Quantized Neural Networks to Global Optimality via Semidefinite Programming
May 05, 2021



Abstract:Neural networks (NNs) have been extremely successful across many tasks in machine learning. Quantization of NN weights has become an important topic due to its impact on their energy efficiency, inference time and deployment on hardware. Although post-training quantization is well-studied, training optimal quantized NNs involves combinatorial non-convex optimization problems which appear intractable. In this work, we introduce a convex optimization strategy to train quantized NNs with polynomial activations. Our method leverages hidden convexity in two-layer neural networks from the recent literature, semidefinite lifting, and Grothendieck's identity. Surprisingly, we show that certain quantized NN problems can be solved to global optimality in polynomial-time in all relevant parameters via semidefinite relaxations. We present numerical examples to illustrate the effectiveness of our method.
Neural Spectrahedra and Semidefinite Lifts: Global Convex Optimization of Polynomial Activation Neural Networks in Fully Polynomial-Time
Jan 07, 2021



Abstract:The training of two-layer neural networks with nonlinear activation functions is an important non-convex optimization problem with numerous applications and promising performance in layerwise deep learning. In this paper, we develop exact convex optimization formulations for two-layer neural networks with second degree polynomial activations based on semidefinite programming. Remarkably, we show that semidefinite lifting is always exact and therefore computational complexity for global optimization is polynomial in the input dimension and sample size for all input data. The developed convex formulations are proven to achieve the same global optimal solution set as their non-convex counterparts. More specifically, the globally optimal two-layer neural network with polynomial activations can be found by solving a semidefinite program (SDP) and decomposing the solution using a procedure we call Neural Decomposition. Moreover, the choice of regularizers plays a crucial role in the computational tractability of neural network training. We show that the standard weight decay regularization formulation is NP-hard, whereas other simple convex penalties render the problem tractable in polynomial time via convex programming. We extend the results beyond the fully connected architecture to different neural network architectures including networks with vector outputs and convolutional architectures with pooling. We provide extensive numerical simulations showing that the standard backpropagation approach often fails to achieve the global optimum of the training loss. The proposed approach is significantly faster to obtain better test accuracy compared to the standard backpropagation procedure.
Debiasing Distributed Second Order Optimization with Surrogate Sketching and Scaled Regularization
Jul 02, 2020



Abstract:In distributed second order optimization, a standard strategy is to average many local estimates, each of which is based on a small sketch or batch of the data. However, the local estimates on each machine are typically biased, relative to the full solution on all of the data, and this can limit the effectiveness of averaging. Here, we introduce a new technique for debiasing the local estimates, which leads to both theoretical and empirical improvements in the convergence rate of distributed second order methods. Our technique has two novel components: (1) modifying standard sketching techniques to obtain what we call a surrogate sketch; and (2) carefully scaling the global regularization parameter for local computations. Our surrogate sketches are based on determinantal point processes, a family of distributions for which the bias of an estimate of the inverse Hessian can be computed exactly. Based on this computation, we show that when the objective being minimized is $l_2$-regularized with parameter $\lambda$ and individual machines are each given a sketch of size $m$, then to eliminate the bias, local estimates should be computed using a shrunk regularization parameter given by $\lambda^{\prime}=\lambda\cdot(1-\frac{d_{\lambda}}{m})$, where $d_{\lambda}$ is the $\lambda$-effective dimension of the Hessian (or, for quadratic problems, the data matrix).
Distributed Averaging Methods for Randomized Second Order Optimization
Feb 16, 2020



Abstract:We consider distributed optimization problems where forming the Hessian is computationally challenging and communication is a significant bottleneck. We develop unbiased parameter averaging methods for randomized second order optimization that employ sampling and sketching of the Hessian. Existing works do not take the bias of the estimators into consideration, which limits their application to massively parallel computation. We provide closed-form formulas for regularization parameters and step sizes that provably minimize the bias for sketched Newton directions. We also extend the framework of second order averaging methods to introduce an unbiased distributed optimization framework for heterogeneous computing systems with varying worker resources. Additionally, we demonstrate the implications of our theoretical findings via large scale experiments performed on a serverless computing platform.
Distributed Sketching Methods for Privacy Preserving Regression
Feb 16, 2020

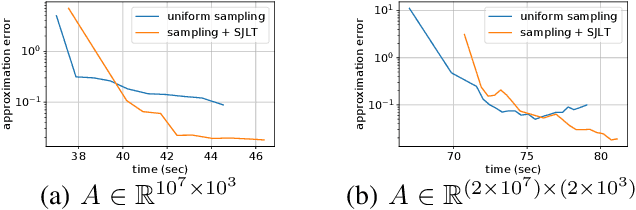
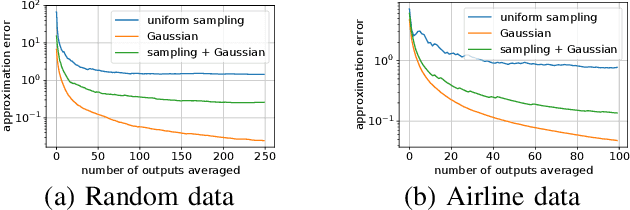
Abstract:In this work, we study distributed sketching methods for large scale regression problems. We leverage multiple randomized sketches for reducing the problem dimensions as well as preserving privacy and improving straggler resilience in asynchronous distributed systems. We derive novel approximation guarantees for classical sketching methods and analyze the accuracy of parameter averaging for distributed sketches. We consider random matrices including Gaussian, randomized Hadamard, uniform sampling and leverage score sampling in the distributed setting. Moreover, we propose a hybrid approach combining sampling and fast random projections for better computational efficiency. We illustrate the performance of distributed sketches in a serverless computing platform with large scale experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge