Distributed Sketching Methods for Privacy Preserving Regression
Paper and Code
Feb 16, 2020

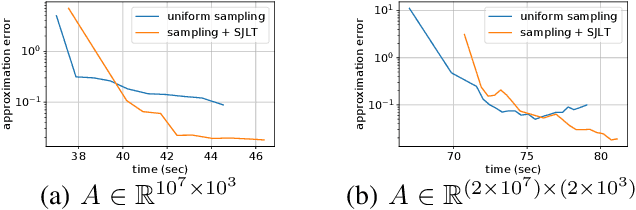
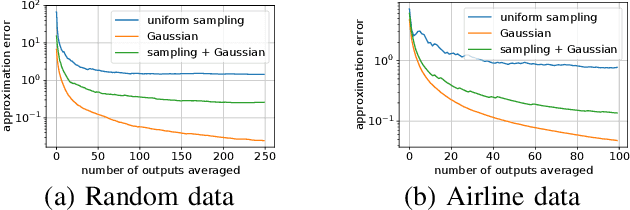
In this work, we study distributed sketching methods for large scale regression problems. We leverage multiple randomized sketches for reducing the problem dimensions as well as preserving privacy and improving straggler resilience in asynchronous distributed systems. We derive novel approximation guarantees for classical sketching methods and analyze the accuracy of parameter averaging for distributed sketches. We consider random matrices including Gaussian, randomized Hadamard, uniform sampling and leverage score sampling in the distributed setting. Moreover, we propose a hybrid approach combining sampling and fast random projections for better computational efficiency. We illustrate the performance of distributed sketches in a serverless computing platform with large scale experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge