Zonghan Wu
A Comprehensive Survey of Knowledge-Based Vision Question Answering Systems: The Lifecycle of Knowledge in Visual Reasoning Task
Apr 24, 2025Abstract:Knowledge-based Vision Question Answering (KB-VQA) extends general Vision Question Answering (VQA) by not only requiring the understanding of visual and textual inputs but also extensive range of knowledge, enabling significant advancements across various real-world applications. KB-VQA introduces unique challenges, including the alignment of heterogeneous information from diverse modalities and sources, the retrieval of relevant knowledge from noisy or large-scale repositories, and the execution of complex reasoning to infer answers from the combined context. With the advancement of Large Language Models (LLMs), KB-VQA systems have also undergone a notable transformation, where LLMs serve as powerful knowledge repositories, retrieval-augmented generators and strong reasoners. Despite substantial progress, no comprehensive survey currently exists that systematically organizes and reviews the existing KB-VQA methods. This survey aims to fill this gap by establishing a structured taxonomy of KB-VQA approaches, and categorizing the systems into main stages: knowledge representation, knowledge retrieval, and knowledge reasoning. By exploring various knowledge integration techniques and identifying persistent challenges, this work also outlines promising future research directions, providing a foundation for advancing KB-VQA models and their applications.
UniRVQA: A Unified Framework for Retrieval-Augmented Vision Question Answering via Self-Reflective Joint Training
Apr 05, 2025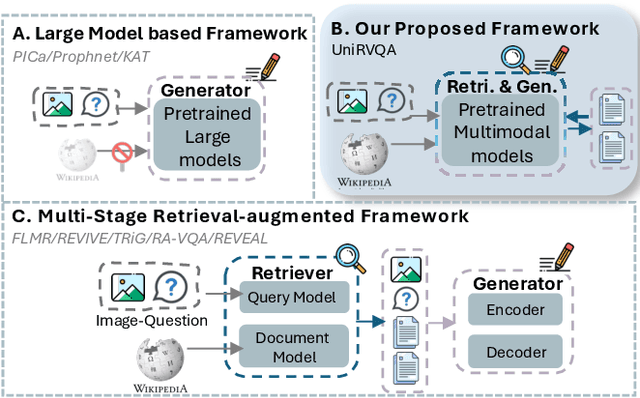
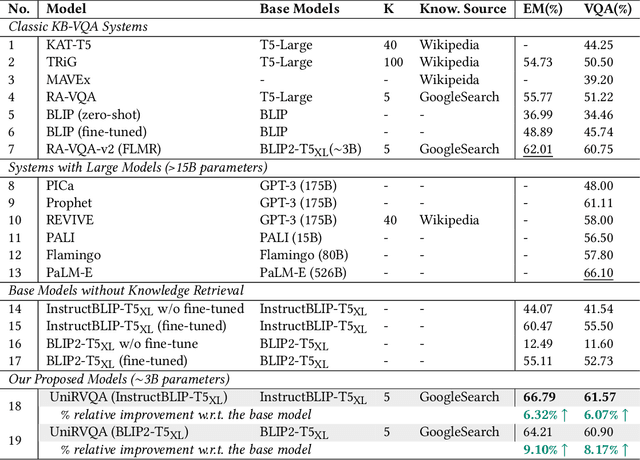
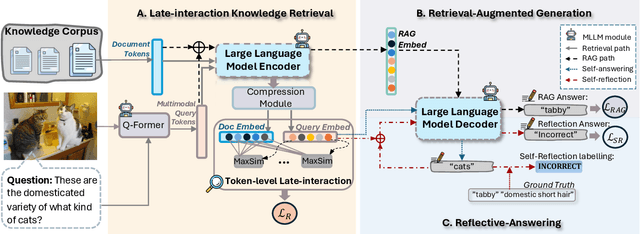
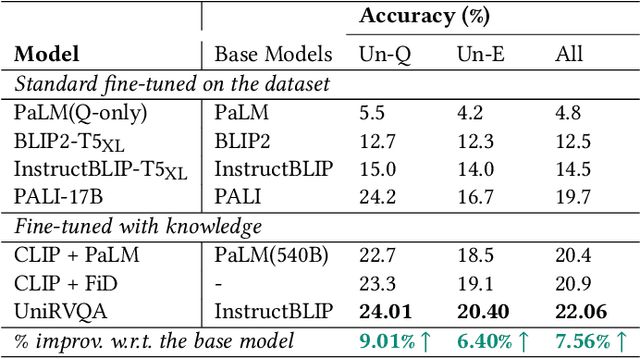
Abstract:Knowledge-based Vision Question Answering (KB-VQA) systems address complex visual-grounded questions requiring external knowledge, such as web-sourced encyclopedia articles. Existing methods often use sequential and separate frameworks for the retriever and the generator with limited parametric knowledge sharing. However, since both retrieval and generation tasks require accurate understanding of contextual and external information, such separation can potentially lead to suboptimal system performance. Another key challenge is the integration of multimodal information. General-purpose multimodal pre-trained models, while adept at multimodal representation learning, struggle with fine-grained retrieval required for knowledge-intensive visual questions. Recent specialized pre-trained models mitigate the issue, but are computationally expensive. To bridge the gap, we propose a Unified Retrieval-Augmented VQA framework (UniRVQA). UniRVQA adapts general multimodal pre-trained models for fine-grained knowledge-intensive tasks within a unified framework, enabling cross-task parametric knowledge sharing and the extension of existing multimodal representation learning capability. We further introduce a reflective-answering mechanism that allows the model to explicitly evaluate and refine its knowledge boundary. Additionally, we integrate late interaction into the retrieval-augmented generation joint training process to enhance fine-grained understanding of queries and documents. Our approach achieves competitive performance against state-of-the-art models, delivering a significant 4.7% improvement in answering accuracy, and brings an average 7.5% boost in base MLLMs' VQA performance.
Personalized Federated Learning With Structure
Mar 08, 2022



Abstract:Knowledge sharing and model personalization are two key components to impact the performance of personalized federated learning (PFL). Existing PFL methods simply treat knowledge sharing as an aggregation of all clients regardless of the hidden relations among them. This paper is to enhance the knowledge-sharing process in PFL by leveraging the structural information among clients. We propose a novel structured federated learning(SFL) framework to simultaneously learn the global model and personalized model using each client's local relations with others and its private dataset. This proposed framework has been formulated to a new optimization problem to model the complex relationship among personalized models and structural topology information into a unified framework. Moreover, in contrast to a pre-defined structure, our framework could be further enhanced by adding a structure learning component to automatically learn the structure using the similarities between clients' models' parameters. By conducting extensive experiments, we first demonstrate how federated learning can be benefited by introducing structural information into the server aggregation process with a real-world dataset, and then the effectiveness of the proposed method has been demonstrated in varying degrees of data non-iid settings.
Spatio-Temporal Joint Graph Convolutional Networks for Traffic Forecasting
Dec 02, 2021
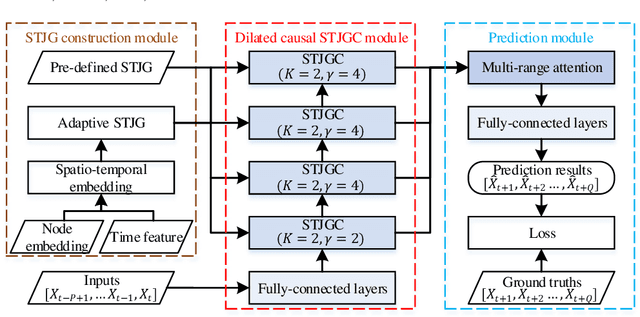

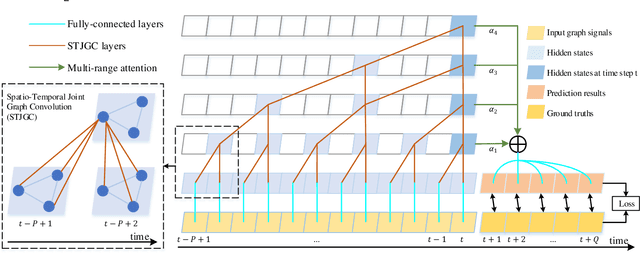
Abstract:Recent studies focus on formulating the traffic forecasting as a spatio-temporal graph modeling problem. They typically construct a static spatial graph at each time step and then connect each node with itself between adjacent time steps to construct the spatio-temporal graph. In such a graph, the correlations between different nodes at different time steps are not explicitly reflected, which may restrict the learning ability of graph neural networks. Meanwhile, those models ignore the dynamic spatio-temporal correlations among nodes as they use the same adjacency matrix at different time steps. To overcome these limitations, we propose a Spatio-Temporal Joint Graph Convolutional Networks (STJGCN) for traffic forecasting over several time steps ahead on a road network. Specifically, we construct both pre-defined and adaptive spatio-temporal joint graphs (STJGs) between any two time steps, which represent comprehensive and dynamic spatio-temporal correlations. We further design dilated causal spatio-temporal joint graph convolution layers on STJG to capture the spatio-temporal dependencies from distinct perspectives with multiple ranges. A multi-range attention mechanism is proposed to aggregate the information of different ranges. Experiments on four public traffic datasets demonstrate that STJGCN is computationally efficient and outperforms 11 state-of-the-art baseline methods.
ConTIG: Continuous Representation Learning on Temporal Interaction Graphs
Sep 27, 2021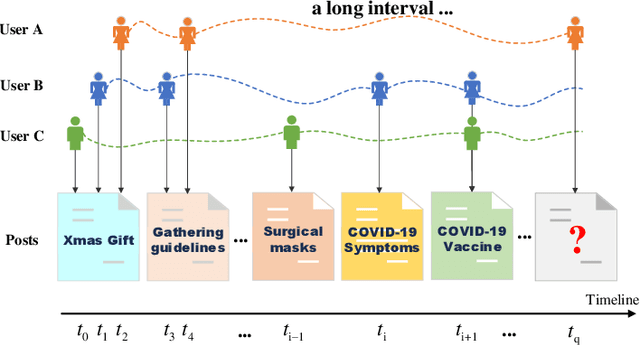
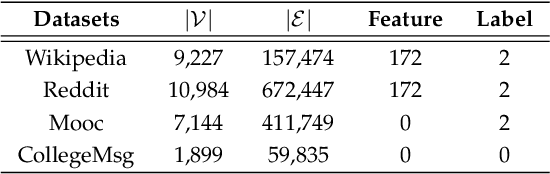
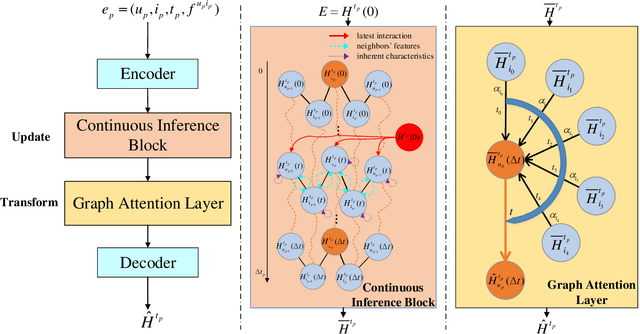
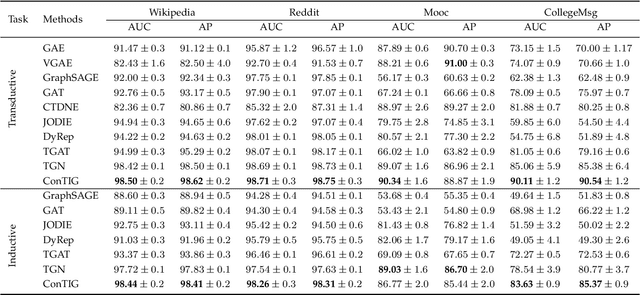
Abstract:Representation learning on temporal interaction graphs (TIG) is to model complex networks with the dynamic evolution of interactions arising in a broad spectrum of problems. Existing dynamic embedding methods on TIG discretely update node embeddings merely when an interaction occurs. They fail to capture the continuous dynamic evolution of embedding trajectories of nodes. In this paper, we propose a two-module framework named ConTIG, a continuous representation method that captures the continuous dynamic evolution of node embedding trajectories. With two essential modules, our model exploit three-fold factors in dynamic networks which include latest interaction, neighbor features and inherent characteristics. In the first update module, we employ a continuous inference block to learn the nodes' state trajectories by learning from time-adjacent interaction patterns between node pairs using ordinary differential equations. In the second transform module, we introduce a self-attention mechanism to predict future node embeddings by aggregating historical temporal interaction information. Experiments results demonstrate the superiority of ConTIG on temporal link prediction, temporal node recommendation and dynamic node classification tasks compared with a range of state-of-the-art baselines, especially for long-interval interactions prediction.
TraverseNet: Unifying Space and Time in Message Passing
Aug 25, 2021



Abstract:This paper aims to unify spatial dependency and temporal dependency in a non-Euclidean space while capturing the inner spatial-temporal dependencies for spatial-temporal graph data. For spatial-temporal attribute entities with topological structure, the space-time is consecutive and unified while each node's current status is influenced by its neighbors' past states over variant periods of each neighbor. Most spatial-temporal neural networks study spatial dependency and temporal correlation separately in processing, gravely impaired the space-time continuum, and ignore the fact that the neighbors' temporal dependency period for a node can be delayed and dynamic. To model this actual condition, we propose TraverseNet, a novel spatial-temporal graph neural network, viewing space and time as an inseparable whole, to mine spatial-temporal graphs while exploiting the evolving spatial-temporal dependencies for each node via message traverse mechanisms. Experiments with ablation and parameter studies have validated the effectiveness of the proposed TraverseNets, and the detailed implementation can be found from https://github.com/nnzhan/TraverseNet.
Beyond Low-pass Filtering: Graph Convolutional Networks with Automatic Filtering
Jul 10, 2021



Abstract:Graph convolutional networks are becoming indispensable for deep learning from graph-structured data. Most of the existing graph convolutional networks share two big shortcomings. First, they are essentially low-pass filters, thus the potentially useful middle and high frequency band of graph signals are ignored. Second, the bandwidth of existing graph convolutional filters is fixed. Parameters of a graph convolutional filter only transform the graph inputs without changing the curvature of a graph convolutional filter function. In reality, we are uncertain about whether we should retain or cut off the frequency at a certain point unless we have expert domain knowledge. In this paper, we propose Automatic Graph Convolutional Networks (AutoGCN) to capture the full spectrum of graph signals and automatically update the bandwidth of graph convolutional filters. While it is based on graph spectral theory, our AutoGCN is also localized in space and has a spatial form. Experimental results show that AutoGCN achieves significant improvement over baseline methods which only work as low-pass filters.
Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks
May 24, 2020



Abstract:Modeling multivariate time series has long been a subject that has attracted researchers from a diverse range of fields including economics, finance, and traffic. A basic assumption behind multivariate time series forecasting is that its variables depend on one another but, upon looking closely, it is fair to say that existing methods fail to fully exploit latent spatial dependencies between pairs of variables. In recent years, meanwhile, graph neural networks (GNNs) have shown high capability in handling relational dependencies. GNNs require well-defined graph structures for information propagation which means they cannot be applied directly for multivariate time series where the dependencies are not known in advance. In this paper, we propose a general graph neural network framework designed specifically for multivariate time series data. Our approach automatically extracts the uni-directed relations among variables through a graph learning module, into which external knowledge like variable attributes can be easily integrated. A novel mix-hop propagation layer and a dilated inception layer are further proposed to capture the spatial and temporal dependencies within the time series. The graph learning, graph convolution, and temporal convolution modules are jointly learned in an end-to-end framework. Experimental results show that our proposed model outperforms the state-of-the-art baseline methods on 3 of 4 benchmark datasets and achieves on-par performance with other approaches on two traffic datasets which provide extra structural information.
Graph WaveNet for Deep Spatial-Temporal Graph Modeling
May 31, 2019



Abstract:Spatial-temporal graph modeling is an important task to analyze the spatial relations and temporal trends of components in a system. Existing approaches mostly capture the spatial dependency on a fixed graph structure, assuming that the underlying relation between entities is pre-determined. However, the explicit graph structure (relation) does not necessarily reflect the true dependency and genuine relation may be missing due to the incomplete connections in the data. Furthermore, existing methods are ineffective to capture the temporal trends as the RNNs or CNNs employed in these methods cannot capture long-range temporal sequences. To overcome these limitations, we propose in this paper a novel graph neural network architecture, Graph WaveNet, for spatial-temporal graph modeling. By developing a novel adaptive dependency matrix and learn it through node embedding, our model can precisely capture the hidden spatial dependency in the data. With a stacked dilated 1D convolution component whose receptive field grows exponentially as the number of layers increases, Graph WaveNet is able to handle very long sequences. These two components are integrated seamlessly in a unified framework and the whole framework is learned in an end-to-end manner. Experimental results on two public traffic network datasets, METR-LA and PEMS-BAY, demonstrate the superior performance of our algorithm.
A Comprehensive Survey on Graph Neural Networks
Jan 03, 2019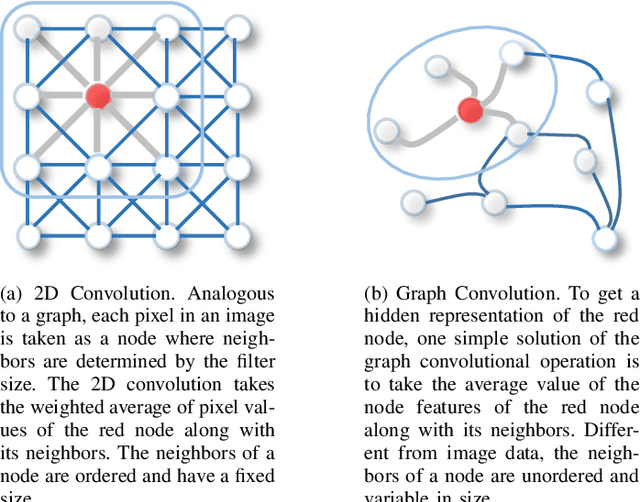
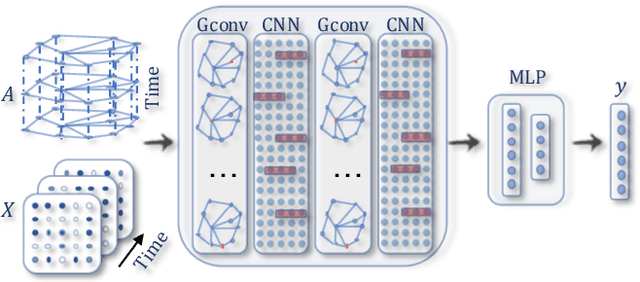

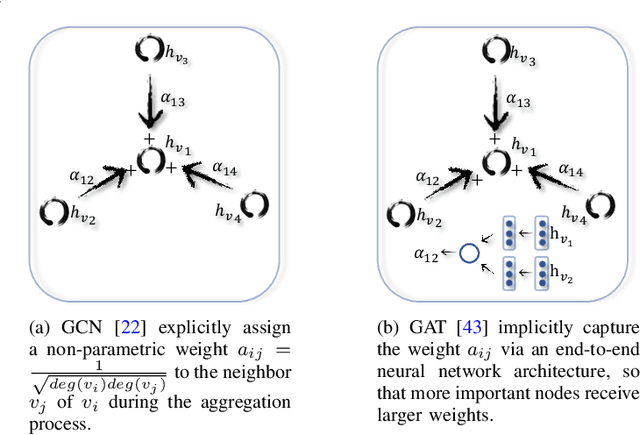
Abstract:Deep learning has revolutionized many machine learning tasks in recent years, ranging from image classification and video processing to speech recognition and natural language understanding. The data in these tasks are typically represented in the Euclidean space. However, there is an increasing number of applications where data are generated from non-Euclidean domains and are represented as graphs with complex relationships and interdependency between objects. The complexity of graph data has imposed significant challenges on existing machine learning algorithms. Recently, many studies on extending deep learning approaches for graph data have emerged. In this survey, we provide a comprehensive overview of graph neural networks (GNNs) in data mining and machine learning fields. We propose a new taxonomy to divide the state-of-the-art graph neural networks into different categories. With a focus on graph convolutional networks, we review alternative architectures that have recently been developed; these learning paradigms include graph attention networks, graph autoencoders, graph generative networks, and graph spatial-temporal networks. We further discuss the applications of graph neural networks across various domains and summarize the open source codes and benchmarks of the existing algorithms on different learning tasks. Finally, we propose potential research directions in this fast-growing field.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge