Zhiying Xu
Quant VideoGen: Auto-Regressive Long Video Generation via 2-Bit KV-Cache Quantization
Feb 03, 2026Abstract:Despite rapid progress in autoregressive video diffusion, an emerging system algorithm bottleneck limits both deployability and generation capability: KV cache memory. In autoregressive video generation models, the KV cache grows with generation history and quickly dominates GPU memory, often exceeding 30 GB, preventing deployment on widely available hardware. More critically, constrained KV cache budgets restrict the effective working memory, directly degrading long horizon consistency in identity, layout, and motion. To address this challenge, we present Quant VideoGen (QVG), a training free KV cache quantization framework for autoregressive video diffusion models. QVG leverages video spatiotemporal redundancy through Semantic Aware Smoothing, producing low magnitude, quantization friendly residuals. It further introduces Progressive Residual Quantization, a coarse to fine multi stage scheme that reduces quantization error while enabling a smooth quality memory trade off. Across LongCat Video, HY WorldPlay, and Self Forcing benchmarks, QVG establishes a new Pareto frontier between quality and memory efficiency, reducing KV cache memory by up to 7.0 times with less than 4% end to end latency overhead while consistently outperforming existing baselines in generation quality.
StreamFusion: Scalable Sequence Parallelism for Distributed Inference of Diffusion Transformers on GPUs
Jan 28, 2026Abstract:Diffusion Transformers (DiTs) have gained increasing adoption in high-quality image and video generation. As demand for higher-resolution images and longer videos increases, single-GPU inference becomes inefficient due to increased latency and large activation sizes. Current frameworks employ sequence parallelism (SP) techniques such as Ulysses Attention and Ring Attention to scale inference. However, these implementations have three primary limitations: (1) suboptimal communication patterns for network topologies on modern GPU machines, (2) latency bottlenecks from all-to-all operations in inter-machine communication, and (3) GPU sender-receiver synchronization and computation overheads from using two-sided communication libraries. To address these issues, we present StreamFusion, a topology-aware efficient DiT serving engine. StreamFusion incorporates three key innovations: (1) a topology-aware sequence parallelism technique that accounts for inter- and intra-machine bandwidth differences, (2) Torus Attention, a novel SP technique enabling overlapping of inter-machine all-to-all operations with computation, and (3) a one-sided communication implementation that minimizes GPU sender-receiver synchronization and computation overheads. Our experiments demonstrate that StreamFusion outperforms the state-of-the-art approach by an average of $1.35\times$ (up to $1.77\times$).
UCCL-EP: Portable Expert-Parallel Communication
Dec 22, 2025Abstract:Mixture-of-Experts (MoE) workloads rely on expert parallelism (EP) to achieve high GPU efficiency. State-of-the-art EP communication systems such as DeepEP demonstrate strong performance but exhibit poor portability across heterogeneous GPU and NIC platforms. The poor portability is rooted in architecture: GPU-initiated token-level RDMA communication requires tight vertical integration between GPUs and NICs, e.g., GPU writes to NIC driver/MMIO interfaces. We present UCCL-EP, a portable EP communication system that delivers DeepEP-level performance across heterogeneous GPU and NIC hardware. UCCL-EP replaces GPU-initiated RDMA with a high-throughput GPU-CPU control channel: compact token-routing commands are transferred to multithreaded CPU proxies, which then issue GPUDirect RDMA operations on behalf of GPUs. UCCL-EP further emulates various ordering semantics required by specialized EP communication modes using RDMA immediate data, enabling correctness on NICs that lack such ordering, e.g., AWS EFA. We implement UCCL-EP on NVIDIA and AMD GPUs with EFA and Broadcom NICs. On EFA, it outperforms the best existing EP solution by up to $2.1\times$ for dispatch and combine throughput. On NVIDIA-only platform, UCCL-EP achieves comparable performance to the original DeepEP. UCCL-EP also improves token throughput on SGLang by up to 40% on the NVIDIA+EFA platform, and improves DeepSeek-V3 training throughput over the AMD Primus/Megatron-LM framework by up to 45% on a 16-node AMD+Broadcom platform.
LEANN: A Low-Storage Vector Index
Jun 09, 2025Abstract:Embedding-based search is widely used in applications such as recommendation and retrieval-augmented generation (RAG). Recently, there is a growing demand to support these capabilities over personal data stored locally on devices. However, maintaining the necessary data structure associated with the embedding-based search is often infeasible due to its high storage overhead. For example, indexing 100 GB of raw data requires 150 to 700 GB of storage, making local deployment impractical. Reducing this overhead while maintaining search quality and latency becomes a critical challenge. In this paper, we present LEANN, a storage-efficient approximate nearest neighbor (ANN) search index optimized for resource-constrained personal devices. LEANN combines a compact graph-based structure with an efficient on-the-fly recomputation strategy to enable fast and accurate retrieval with minimal storage overhead. Our evaluation shows that LEANN reduces index size to under 5% of the original raw data, achieving up to 50 times smaller storage than standard indexes, while maintaining 90% top-3 recall in under 2 seconds on real-world question answering benchmarks.
Qwen2.5-1M Technical Report
Jan 26, 2025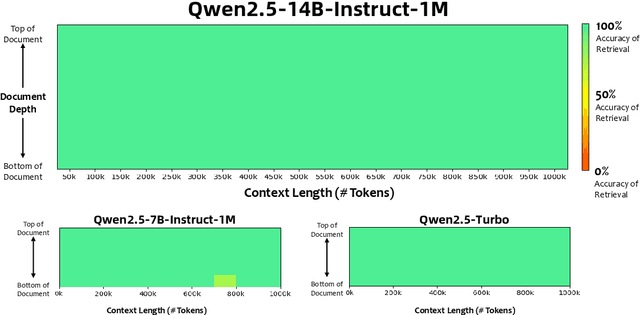

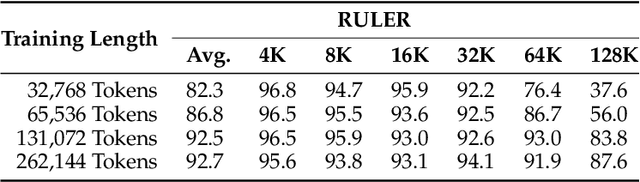
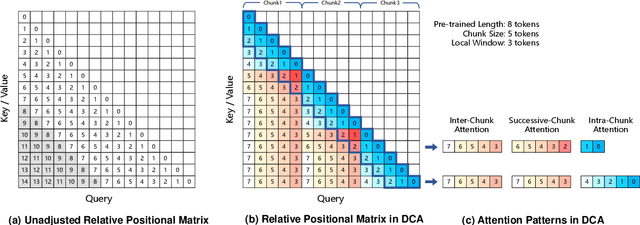
Abstract:We introduce Qwen2.5-1M, a series of models that extend the context length to 1 million tokens. Compared to the previous 128K version, the Qwen2.5-1M series have significantly enhanced long-context capabilities through long-context pre-training and post-training. Key techniques such as long data synthesis, progressive pre-training, and multi-stage supervised fine-tuning are employed to effectively enhance long-context performance while reducing training costs. To promote the use of long-context models among a broader user base, we present and open-source our inference framework. This framework includes a length extrapolation method that can expand the model context lengths by at least four times, or even more, without additional training. To reduce inference costs, we implement a sparse attention method along with chunked prefill optimization for deployment scenarios and a sparsity refinement method to improve precision. Additionally, we detail our optimizations in the inference engine, including kernel optimization, pipeline parallelism, and scheduling optimization, which significantly enhance overall inference performance. By leveraging our inference framework, the Qwen2.5-1M models achieve a remarkable 3x to 7x prefill speedup in scenarios with 1 million tokens of context. This framework provides an efficient and powerful solution for developing applications that require long-context processing using open-source models. The Qwen2.5-1M series currently includes the open-source models Qwen2.5-7B-Instruct-1M and Qwen2.5-14B-Instruct-1M, as well as the API-accessed model Qwen2.5-Turbo. Evaluations show that Qwen2.5-1M models have been greatly improved in long-context tasks without compromising performance in short-context scenarios. Specifically, the Qwen2.5-14B-Instruct-1M model significantly outperforms GPT-4o-mini in long-context tasks and supports contexts eight times longer.
NetFlowGen: Leveraging Generative Pre-training for Network Traffic Dynamics
Dec 30, 2024Abstract:Understanding the traffic dynamics in networks is a core capability for automated systems to monitor and analyze networking behaviors, reducing expensive human efforts and economic risks through tasks such as traffic classification, congestion prediction, and attack detection. However, it is still challenging to accurately model network traffic with machine learning approaches in an efficient and broadly applicable manner. Task-specific models trained from scratch are used for different networking applications, which limits the efficiency of model development and generalization of model deployment. Furthermore, while networking data is abundant, high-quality task-specific labels are often insufficient for training individual models. Large-scale self-supervised learning on unlabeled data provides a natural pathway for tackling these challenges. We propose to pre-train a general-purpose machine learning model to capture traffic dynamics with only traffic data from NetFlow records, with the goal of fine-tuning for different downstream tasks with small amount of labels. Our presented NetFlowGen framework goes beyond a proof-of-concept for network traffic pre-training and addresses specific challenges such as unifying network feature representations, learning from large unlabeled traffic data volume, and testing on real downstream tasks in DDoS attack detection. Experiments demonstrate promising results of our pre-training framework on capturing traffic dynamics and adapting to different networking tasks.
AGO: Boosting Mobile AI Inference Performance by Removing Constraints on Graph Optimization
Dec 02, 2022Abstract:Traditional deep learning compilers rely on heuristics for subgraph generation, which impose extra constraints on graph optimization, e.g., each subgraph can only contain at most one complex operator. In this paper, we propose AGO, a framework for graph optimization with arbitrary structures to boost the inference performance of deep models by removing such constraints. To create new optimization opportunities for complicated subgraphs, we propose intensive operator fusion, which can effectively stitch multiple complex operators together for better performance. Further, we design a graph partitioning scheme that allows an arbitrary structure for each subgraph while guaranteeing the acyclic property among all generated subgraphs. Additionally, to enable efficient performance tuning on complicated subgraphs, we devise a novel divide-and-conquer tuning mechanism to orchestrate different system components. Through extensive experiments on various neural networks and mobile devices, we show that our system can improve the inference performance by up to 3.3x when compared with state-of-the-art deep compilers.
Teal: Learning-Accelerated Optimization of Traffic Engineering
Oct 25, 2022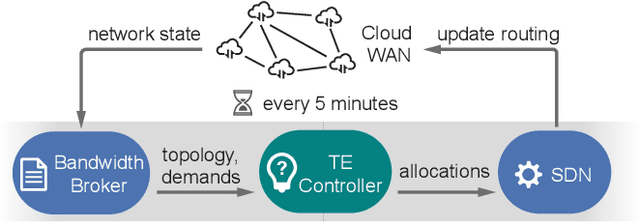
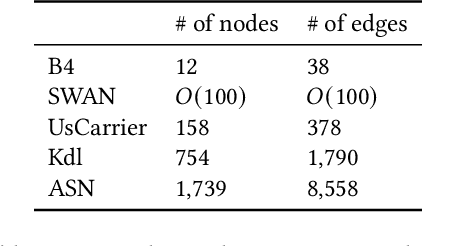
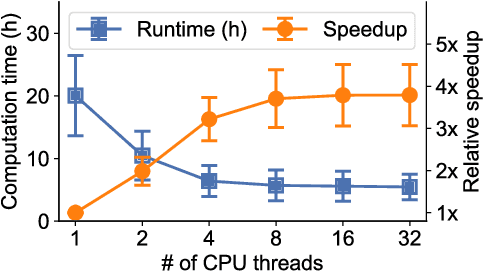

Abstract:In the last decade, global cloud wide-area networks (WANs) have grown 10$\times$ in size due to the deployment of new network sites and datacenters, making it challenging for commercial optimization engines to solve the network traffic engineering (TE) problem within the temporal budget of a few minutes. In this work, we show that carefully designed deep learning models are key to accelerating the running time of intra-WAN TE systems for large deployments since deep learning is both massively parallel and it benefits from the wealth of historical traffic allocation data from production WANs. However, off-the-shelf deep learning methods fail to perform well on the TE task since they ignore the effects of network connectivity on flow allocations. They are also faced with a tractability challenge posed by the large problem scale of TE optimization. Moreover, neural networks do not have mechanisms to readily enforce hard constraints on model outputs (e.g., link capacity constraints). We tackle these challenges by designing a deep learning-based TE system -- Teal. First, Teal leverages graph neural networks (GNN) to faithfully capture connectivity and model network flows. Second, Teal devises a multi-agent reinforcement learning (RL) algorithm to process individual demands independently in parallel to lower the problem scale. Finally, Teal reduces link capacity violations and improves solution quality using the alternating direction method of multipliers (ADMM). We evaluate Teal on traffic matrices of a global commercial cloud provider and find that Teal computes near-optimal traffic allocations with a 59$\times$ speedup over state-of-the-art TE systems on a WAN topology of over 1,500 nodes.
Automating Botnet Detection with Graph Neural Networks
Mar 13, 2020
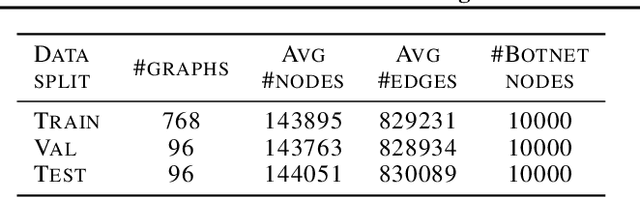
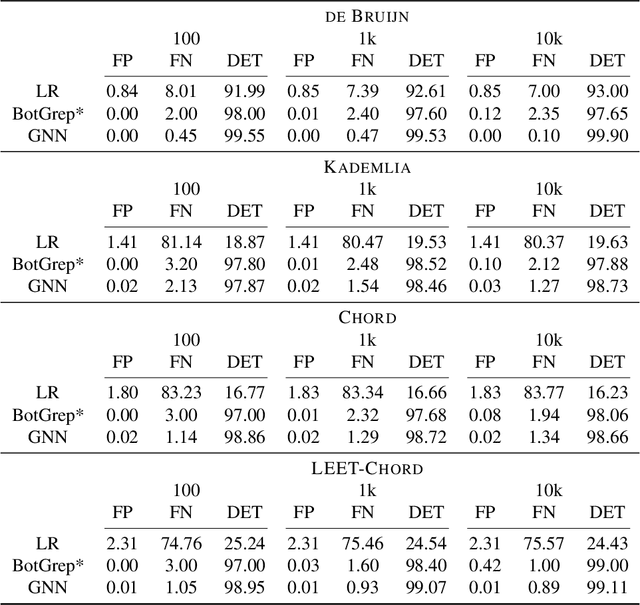
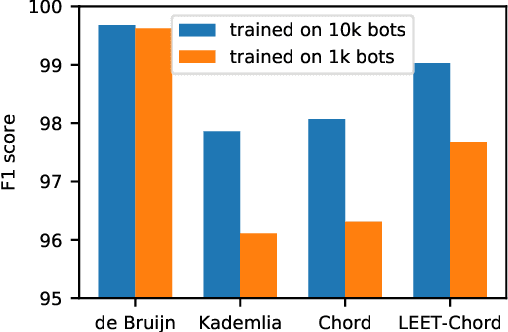
Abstract:Botnets are now a major source for many network attacks, such as DDoS attacks and spam. However, most traditional detection methods heavily rely on heuristically designed multi-stage detection criteria. In this paper, we consider the neural network design challenges of using modern deep learning techniques to learn policies for botnet detection automatically. To generate training data, we synthesize botnet connections with different underlying communication patterns overlaid on large-scale real networks as datasets. To capture the important hierarchical structure of centralized botnets and the fast-mixing structure for decentralized botnets, we tailor graph neural networks (GNN) to detect the properties of these structures. Experimental results show that GNNs are better able to capture botnet structure than previous non-learning methods when trained with appropriate data, and that deeper GNNs are crucial for learning difficult botnet topologies. We believe our data and studies can be useful for both the network security and graph learning communities.
* Data and code available https://github.com/harvardnlp/botnet-detection . Accepted as a workshop paper in MLSys 2020 Conference
An Adaptive and Fast Convergent Approach to Differentially Private Deep Learning
Dec 19, 2019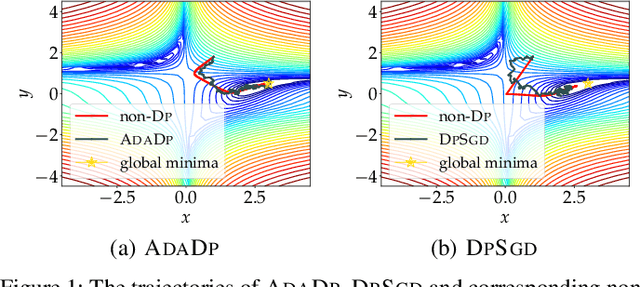
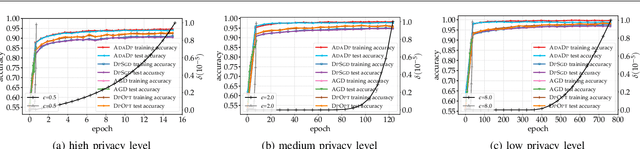
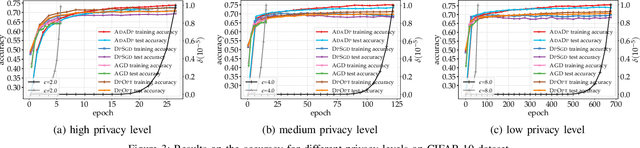
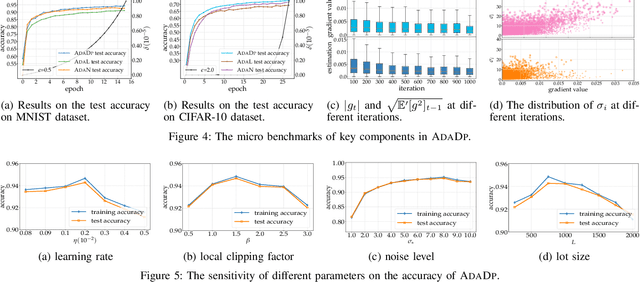
Abstract:With the advent of the era of big data, deep learning has become a prevalent building block in a variety of machine learning or data mining tasks, such as signal processing, network modeling and traffic analysis, to name a few. The massive user data crowdsourced plays a crucial role in the success of deep learning models. However, it has been shown that user data may be inferred from trained neural models and thereby exposed to potential adversaries, which raises information security and privacy concerns. To address this issue, recent studies leverage the technique of differential privacy to design private-preserving deep learning algorithms. Albeit successful at privacy protection, differential privacy degrades the performance of neural models. In this paper, we develop ADADP, an adaptive and fast convergent learning algorithm with a provable privacy guarantee. ADADP significantly reduces the privacy cost by improving the convergence speed with an adaptive learning rate and mitigates the negative effect of differential privacy upon the model accuracy by introducing adaptive noise. The performance of ADADP is evaluated on real-world datasets. Experiment results show that it outperforms state-of-the-art differentially private approaches in terms of both privacy cost and model accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge