Reviewing and Improving the Gaussian Mechanism for Differential Privacy
Paper and Code
Dec 07, 2019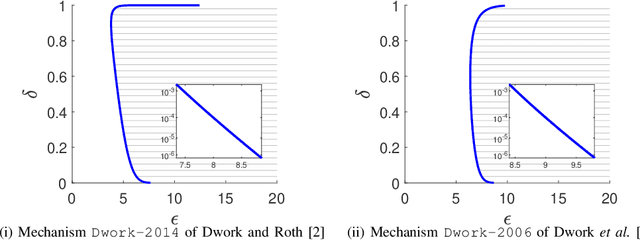
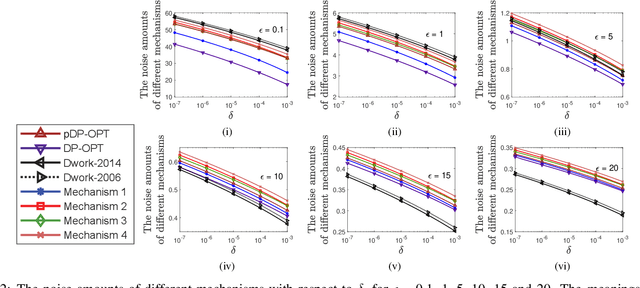
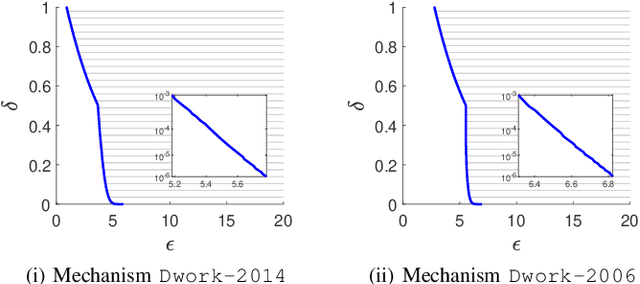
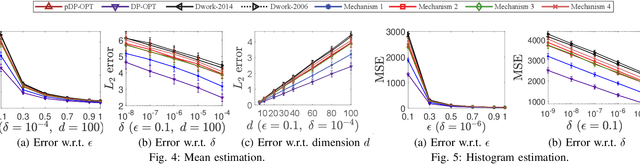
Differential privacy provides a rigorous framework to quantify data privacy, and has received considerable interest recently. A randomized mechanism satisfying $(\epsilon, \delta)$-differential privacy (DP) roughly means that, except with a small probability $\delta$, altering a record in a dataset cannot change the probability that an output is seen by more than a multiplicative factor $e^{\epsilon} $. A well-known solution to $(\epsilon, \delta)$-DP is the Gaussian mechanism initiated by Dwork et al. [1] in 2006 with an improvement by Dwork and Roth [2] in 2014, where a Gaussian noise amount $\sqrt{2\ln \frac{2}{\delta}} \times \frac{\Delta}{\epsilon}$ of [1] or $\sqrt{2\ln \frac{1.25}{\delta}} \times \frac{\Delta}{\epsilon}$ of [2] is added independently to each dimension of the query result, for a query with $\ell_2$-sensitivity $\Delta$. Although both classical Gaussian mechanisms [1,2] assume $0 < \epsilon \leq 1$, our review finds that many studies in the literature have used the classical Gaussian mechanisms under values of $\epsilon$ and $\delta$ where the added noise amounts of [1,2] do not achieve $(\epsilon,\delta)$-DP. We obtain such result by analyzing the optimal noise amount $\sigma_{DP-OPT}$ for $(\epsilon,\delta)$-DP and identifying $\epsilon$ and $\delta$ where the noise amounts of classical mechanisms are even less than $\sigma_{DP-OPT}$. Since $\sigma_{DP-OPT}$ has no closed-form expression and needs to be approximated in an iterative manner, we propose Gaussian mechanisms by deriving closed-form upper bounds for $\sigma_{DP-OPT}$. Our mechanisms achieve $(\epsilon,\delta)$-DP for any $\epsilon$, while the classical mechanisms [1,2] do not achieve $(\epsilon,\delta)$-DP for large $\epsilon$ given $\delta$. Moreover, the utilities of our mechanisms improve those of [1,2] and are close to that of the optimal yet more computationally expensive Gaussian mechanism.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge