A Neural Tangent Kernel View on Federated Averaging for Deep Linear Neural Network

Federated averaging (FedAvg) is a widely employed paradigm for collaboratively training models from distributed clients without sharing data. Nowadays, the neural network has achieved remarkable success due to its extraordinary performance, which makes it a preferred choice as the model in FedAvg. However, the optimization problem of the neural network is often non-convex even non-smooth. Furthermore, FedAvg always involves multiple clients and local updates, which results in an inaccurate updating direction. These properties bring difficulties in analyzing the convergence of FedAvg in training neural networks. Recently, neural tangent kernel (NTK) theory has been proposed towards understanding the convergence of first-order methods in tackling the non-convex problem of neural networks. The deep linear neural network is a classical model in theoretical subject due to its simple formulation. Nevertheless, there exists no theoretical result for the convergence of FedAvg in training the deep linear neural network. By applying NTK theory, we make a further step to provide the first theoretical guarantee for the global convergence of FedAvg in training deep linear neural networks. Specifically, we prove FedAvg converges to the global minimum at a linear rate $\mathcal{O}\big((1-\eta K /N)^t\big)$, where $t$ is the number of iterations, $\eta$ is the learning rate, $N$ is the number of clients and $K$ is the number of local updates. Finally, experimental evaluations on two benchmark datasets are conducted to empirically validate the correctness of our theoretical findings.

A high-resolution dynamical view on momentum methods for over-parameterized neural networks

In this paper, we present the convergence analysis of momentum methods in training a two-layer over-parameterized ReLU neural network, where the number of parameters is significantly larger than that of training instances. Existing works on momentum methods show that the heavy-ball method (HB) and Nesterov's accelerated method (NAG) share the same limiting ordinary differential equation (ODE), which leads to identical convergence rate. From a high-resolution dynamical view, we show that HB differs from NAG in terms of the convergence rate. In addition, our findings provide tighter upper bounds on convergence for the high-resolution ODEs of HB and NAG.

FedSSO: A Federated Server-Side Second-Order Optimization Algorithm

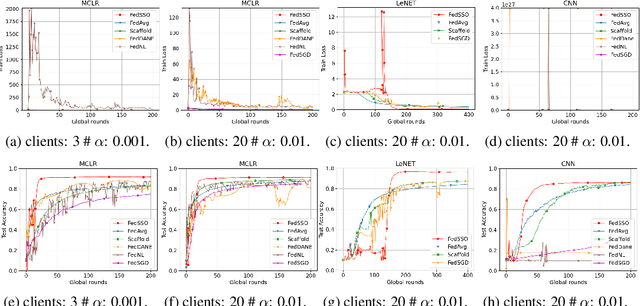
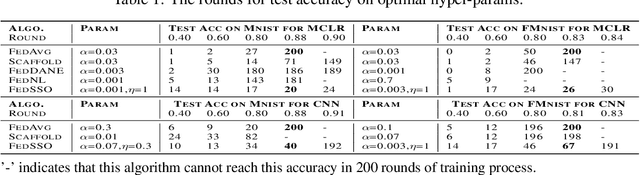
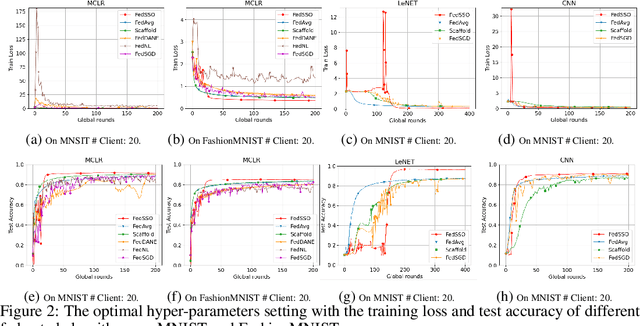
In this work, we propose FedSSO, a server-side second-order optimization method for federated learning (FL). In contrast to previous works in this direction, we employ a server-side approximation for the Quasi-Newton method without requiring any training data from the clients. In this way, we not only shift the computation burden from clients to server, but also eliminate the additional communication for second-order updates between clients and server entirely. We provide theoretical guarantee for convergence of our novel method, and empirically demonstrate our fast convergence and communication savings in both convex and non-convex settings.

Multiple Domain Cyberspace Attack and Defense Game Based on Reward Randomization Reinforcement Learning

The existing network attack and defense method can be regarded as game, but most of the game only involves network domain, not multiple domain cyberspace. To address this challenge, this paper proposed a multiple domain cyberspace attack and defense game model based on reinforcement learning. We define the multiple domain cyberspace include physical domain, network domain and digital domain. By establishing two agents, representing the attacker and the defender respectively, defender will select the multiple domain actions in the multiple domain cyberspace to obtain defender's optimal reward by reinforcement learning. In order to improve the defense ability of defender, a game model based on reward randomization reinforcement learning is proposed. When the defender takes the multiple domain defense action, the reward is randomly given and subject to linear distribution, so as to find the better defense policy and improve defense success rate. The experimental results show that the game model can effectively simulate the attack and defense state of multiple domain cyberspace, and the proposed method has a higher defense success rate than DDPG and DQN.

KGRGRL: A User's Permission Reasoning Method Based on Knowledge Graph Reward Guidance Reinforcement Learning

In general, multiple domain cyberspace security assessments can be implemented by reasoning user's permissions. However, while existing methods include some information from the physical and social domains, they do not provide a comprehensive representation of cyberspace. Existing reasoning methods are also based on expert-given rules, resulting in inefficiency and a low degree of intelligence. To address this challenge, we create a Knowledge Graph (KG) of multiple domain cyberspace in order to provide a standard semantic description of the multiple domain cyberspace. Following that, we proposed a user's permissions reasoning method based on reinforcement learning. All permissions in cyberspace are represented as nodes, and an agent is trained to find all permissions that user can have according to user's initial permissions and cyberspace KG. We set 10 reward setting rules based on the features of cyberspace KG in the reinforcement learning of reward information setting, so that the agent can better locate user's all permissions and avoid blindly finding user's permissions. The results of the experiments showed that the proposed method can successfully reason about user's permissions and increase the intelligence level of the user's permissions reasoning method. At the same time, the F1 value of the proposed method is 6% greater than that of the Translating Embedding (TransE) method.

A Convergence Analysis of Nesterov's Accelerated Gradient Method in Training Deep Linear Neural Networks

Momentum methods, including heavy-ball~(HB) and Nesterov's accelerated gradient~(NAG), are widely used in training neural networks for their fast convergence. However, there is a lack of theoretical guarantees for their convergence and acceleration since the optimization landscape of the neural network is non-convex. Nowadays, some works make progress towards understanding the convergence of momentum methods in an over-parameterized regime, where the number of the parameters exceeds that of the training instances. Nonetheless, current results mainly focus on the two-layer neural network, which are far from explaining the remarkable success of the momentum methods in training deep neural networks. Motivated by this, we investigate the convergence of NAG with constant learning rate and momentum parameter in training two architectures of deep linear networks: deep fully-connected linear neural networks and deep linear ResNets. Based on the over-parameterization regime, we first analyze the residual dynamics induced by the training trajectory of NAG for a deep fully-connected linear neural network under the random Gaussian initialization. Our results show that NAG can converge to the global minimum at a $(1 - \mathcal{O}(1/\sqrt{\kappa}))^t$ rate, where $t$ is the iteration number and $\kappa > 1$ is a constant depending on the condition number of the feature matrix. Compared to the $(1 - \mathcal{O}(1/{\kappa}))^t$ rate of GD, NAG achieves an acceleration over GD. To the best of our knowledge, this is the first theoretical guarantee for the convergence of NAG to the global minimum in training deep neural networks. Furthermore, we extend our analysis to deep linear ResNets and derive a similar convergence result.

Adversarial Attack via Dual-Stage Network Erosion

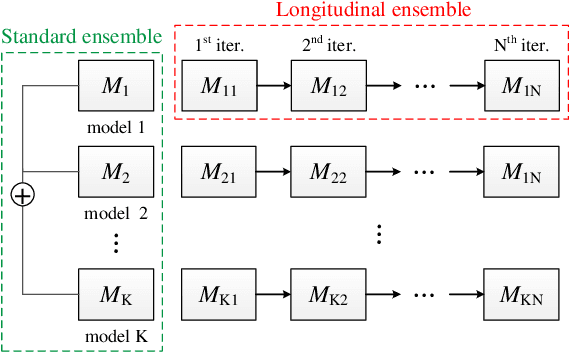
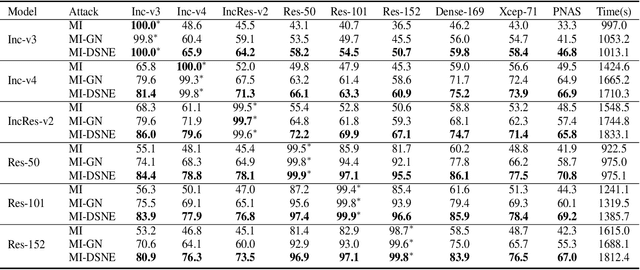
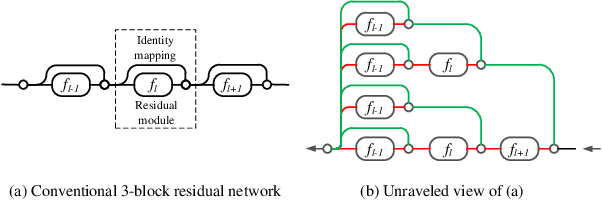
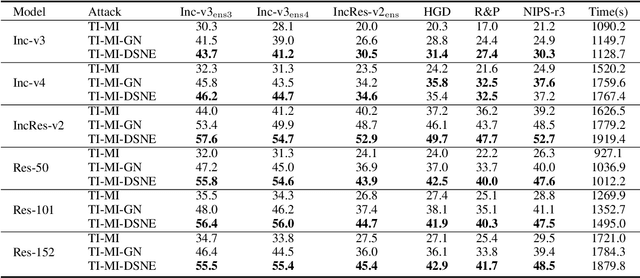
Deep neural networks are vulnerable to adversarial examples, which can fool deep models by adding subtle perturbations. Although existing attacks have achieved promising results, it still leaves a long way to go for generating transferable adversarial examples under the black-box setting. To this end, this paper proposes to improve the transferability of adversarial examples, and applies dual-stage feature-level perturbations to an existing model to implicitly create a set of diverse models. Then these models are fused by the longitudinal ensemble during the iterations. The proposed method is termed Dual-Stage Network Erosion (DSNE). We conduct comprehensive experiments both on non-residual and residual networks, and obtain more transferable adversarial examples with the computational cost similar to the state-of-the-art method. In particular, for the residual networks, the transferability of the adversarial examples can be significantly improved by biasing the residual block information to the skip connections. Our work provides new insights into the architectural vulnerability of neural networks and presents new challenges to the robustness of neural networks.

Improving the Transferability of Adversarial Examples with Resized-Diverse-Inputs, Diversity-Ensemble and Region Fitting

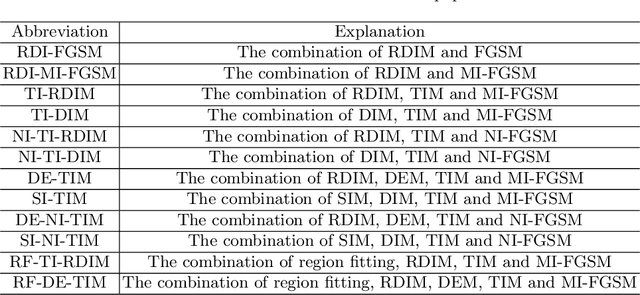
We introduce a three stage pipeline: resized-diverse-inputs (RDIM), diversity-ensemble (DEM) and region fitting, that work together to generate transferable adversarial examples. We first explore the internal relationship between existing attacks, and propose RDIM that is capable of exploiting this relationship. Then we propose DEM, the multi-scale version of RDIM, to generate multi-scale gradients. After the first two steps we transform value fitting into region fitting across iterations. RDIM and region fitting do not require extra running time and these three steps can be well integrated into other attacks. Our best attack fools six black-box defenses with a 93% success rate on average, which is higher than the state-of-the-art gradient-based attacks. Besides, we rethink existing attacks rather than simply stacking new methods on the old ones to get better performance. It is expected that our findings will serve as the beginning of exploring the internal relationship between attack methods. Codes are available at https://github.com/278287847/DEM.

DPA: Learning Robust Physical Adversarial Camouflages for Object Detectors

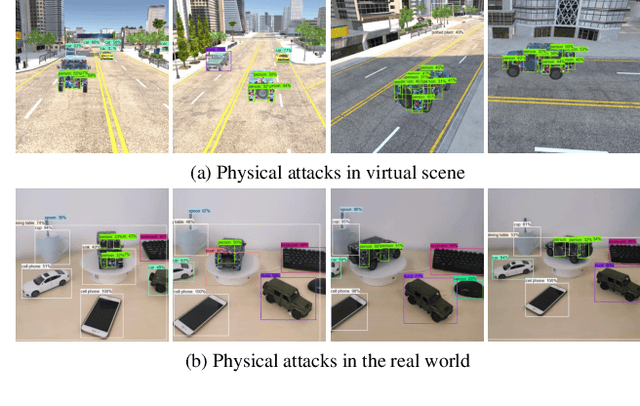
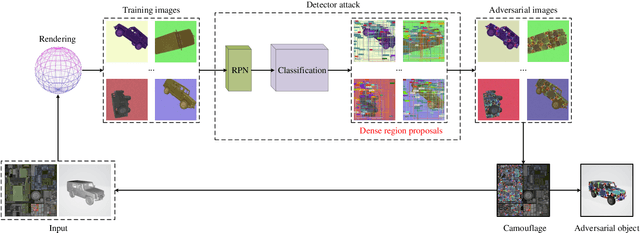
Adversarial attacks are feasible in the real world for object detection. However, most of the previous works have tried to learn "patches" applied to an object to fool detectors, which become less effective or even ineffective in squint view angles. To address this issue, we propose the Dense Proposals Attack (DPA) to learn robust, physical and targeted adversarial camouflages for detectors. The camouflages are robust because they remain adversarial when filmed under arbitrary viewpoint and different illumination conditions, physical because they function well both in the 3D virtual scene and the real world, and targeted because they can cause detectors to misidentify an object as a specific target class. In order to make the generated camouflages robust in the physical world, we introduce a combination of viewpoint shifts, lighting and other natural transformations to model the physical phenomena. In addition, to improve the attacks, DPA substantially attacks all the classifications in the fixed region proposals. Moreover, we build a virtual 3D scene using the Unity simulation engine to fairly and reproducibly evaluate different physical attacks. Extensive experiments demonstrate that DPA outperforms the state-of-the-art methods significantly, and generalizes well to the real world, posing a potential threat to the security-critical computer vision systems.

Provable Convergence of Nesterov Accelerated Method for Over-Parameterized Neural Networks

Despite the empirical success of deep learning, it still lacks theoretical understandings to explain why randomly initialized neural network trained by first-order optimization methods is able to achieve zero training loss, even though its landscape is non-convex and non-smooth. Recently, there are some works to demystifies this phenomenon under over-parameterized regime. In this work, we make further progress on this area by considering a commonly used momentum optimization algorithm: Nesterov accelerated method (NAG). We analyze the convergence of NAG for two-layer fully connected neural network with ReLU activation. Specifically, we prove that the error of NAG converges to zero at a linear convergence rate $1-\Theta(1/\sqrt{\kappa})$, where $\kappa > 1$ is determined by the initialization and the architecture of neural network. Comparing to the rate $1-\Theta(1/\kappa)$ of gradient descent, NAG achieves an acceleration. Besides, it also validates NAG and Heavy-ball method can achieve a similar convergence rate.