Exact: Exploring Space-Time Perceptive Clues for Weakly Supervised Satellite Image Time Series Semantic Segmentation

Automated crop mapping through Satellite Image Time Series (SITS) has emerged as a crucial avenue for agricultural monitoring and management. However, due to the low resolution and unclear parcel boundaries, annotating pixel-level masks is exceptionally complex and time-consuming in SITS. This paper embraces the weakly supervised paradigm (i.e., only image-level categories available) to liberate the crop mapping task from the exhaustive annotation burden. The unique characteristics of SITS give rise to several challenges in weakly supervised learning: (1) noise perturbation from spatially neighboring regions, and (2) erroneous semantic bias from anomalous temporal periods. To address the above difficulties, we propose a novel method, termed exploring space-time perceptive clues (Exact). First, we introduce a set of spatial clues to explicitly capture the representative patterns of different crops from the most class-relative regions. Besides, we leverage the temporal-to-class interaction of the model to emphasize the contributions of pivotal clips, thereby enhancing the model perception for crop regions. Build upon the space-time perceptive clues, we derive the clue-based CAMs to effectively supervise the SITS segmentation network. Our method demonstrates impressive performance on various SITS benchmarks. Remarkably, the segmentation network trained on Exact-generated masks achieves 95% of its fully supervised performance, showing the bright promise of weakly supervised paradigm in crop mapping scenario. Our code will be publicly available.

TopoLogic: An Interpretable Pipeline for Lane Topology Reasoning on Driving Scenes

As an emerging task that integrates perception and reasoning, topology reasoning in autonomous driving scenes has recently garnered widespread attention. However, existing work often emphasizes "perception over reasoning": they typically boost reasoning performance by enhancing the perception of lanes and directly adopt MLP to learn lane topology from lane query. This paradigm overlooks the geometric features intrinsic to the lanes themselves and are prone to being influenced by inherent endpoint shifts in lane detection. To tackle this issue, we propose an interpretable method for lane topology reasoning based on lane geometric distance and lane query similarity, named TopoLogic. This method mitigates the impact of endpoint shifts in geometric space, and introduces explicit similarity calculation in semantic space as a complement. By integrating results from both spaces, our methods provides more comprehensive information for lane topology. Ultimately, our approach significantly outperforms the existing state-of-the-art methods on the mainstream benchmark OpenLane-V2 (23.9 v.s. 10.9 in TOP$_{ll}$ and 44.1 v.s. 39.8 in OLS on subset_A. Additionally, our proposed geometric distance topology reasoning method can be incorporated into well-trained models without re-training, significantly boost the performance of lane topology reasoning. The code is released at https://github.com/Franpin/TopoLogic.

Rethinking Boundary Discontinuity Problem for Oriented Object Detection

Oriented object detection has been developed rapidly in the past few years, where rotation equivariant is crucial for detectors to predict rotated bounding boxes. It is expected that the prediction can maintain the corresponding rotation when objects rotate, but severe mutational in angular prediction is sometimes observed when objects rotate near the boundary angle, which is well-known boundary discontinuity problem. The problem has been long believed to be caused by the sharp loss increase at the angular boundary during training, and widely used IoU-like loss generally deal with this problem by loss-smoothing. However, we experimentally find that even state-of-the-art IoU-like methods do not actually solve the problem. On further analysis, we find the essential cause of the problem lies at discontinuous angular ground-truth(box), not just discontinuous loss. There always exists an irreparable gap between continuous model ouput and discontinuous angular ground-truth, so angular prediction near the breakpoints becomes highly unstable, which cannot be eliminated just by loss-smoothing in IoU-like methods. To thoroughly solve this problem, we propose a simple and effective Angle Correct Module (ACM) based on polar coordinate decomposition. ACM can be easily plugged into the workflow of oriented object detectors to repair angular prediction. It converts the smooth value of the model output into sawtooth angular value, and then IoU-like loss can fully release their potential. Extensive experiments on multiple datasets show that whether Gaussian-based or SkewIoU methods are improved to the same performance of AP50 and AP75 with the enhancement of ACM.

Unbiased IoU for Spherical Image Object Detection

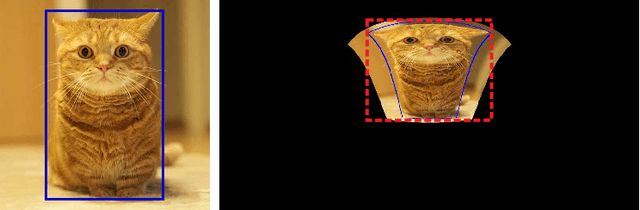
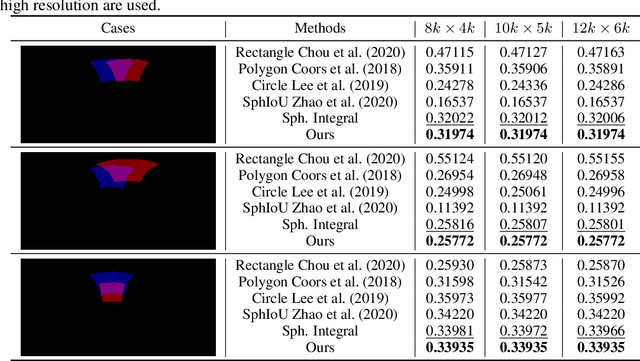
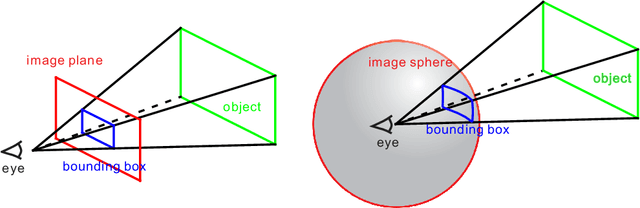
As one of the most fundamental and challenging problems in computer vision, object detection tries to locate object instances and find their categories in natural images. The most important step in the evaluation of object detection algorithm is calculating the intersection-over-union (IoU) between the predicted bounding box and the ground truth one. Although this procedure is well-defined and solved for planar images, it is not easy for spherical image object detection. Existing methods either compute the IoUs based on biased bounding box representations or make excessive approximations, thus would give incorrect results. In this paper, we first identify that spherical rectangles are unbiased bounding boxes for objects in spherical images, and then propose an analytical method for IoU calculation without any approximations. Based on the unbiased representation and calculation, we also present an anchor free object detection algorithm for spherical images. The experiments on two spherical object detection datasets show that the proposed method can achieve better performance than existing methods.

Dense Scale Network for Crowd Counting

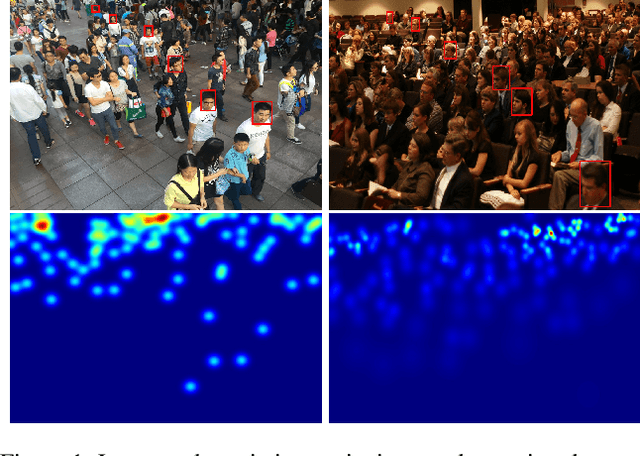
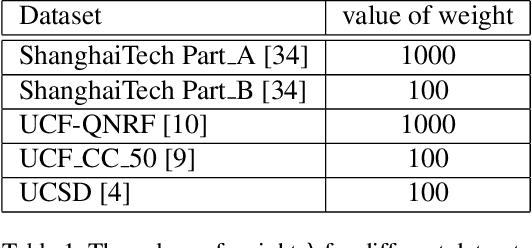
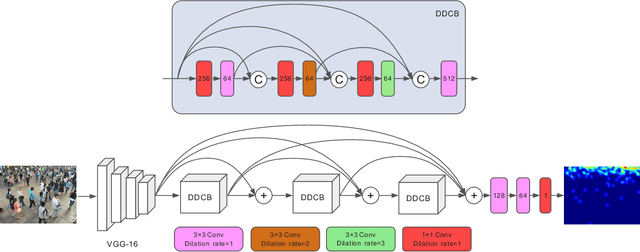
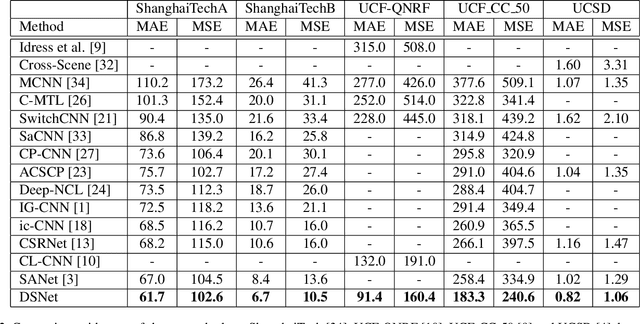
Crowd counting has been widely studied by computer vision community in recent years. Due to the large scale variation, it remains to be a challenging task. Previous methods adopt either multi-column CNN or single-column CNN with multiple branches to deal with this problem. However, restricted by the number of columns or branches, these methods can only capture a few different scales and have limited capability. In this paper, we propose a simple but effective network called DSNet for crowd counting, which can be easily trained in an end-to-end fashion. The key component of our network is the dense dilated convolution block, in which each dilation layer is densely connected with the others to preserve information from continuously varied scales. The dilation rates in dilation layers are carefully selected to prevent the block from gridding artifacts. To further enlarge the range of scales covered by the network, we cascade three blocks and link them with dense residual connections. We also introduce a novel multi-scale density level consistency loss for performance improvement. To evaluate our method, we compare it with state-of-the-art algorithms on four crowd counting datasets (ShanghaiTech, UCF-QNRF, UCF_CC_50 and UCSD). Experimental results demonstrate that DSNet can achieve the best performance and make significant improvements on all the four datasets (30% on the UCF-QNRF and UCF_CC_50, and 20% on the others).

DR2-Net: Deep Residual Reconstruction Network for Image Compressive Sensing

Most traditional algorithms for compressive sensing image reconstruction suffer from the intensive computation. Recently, deep learning-based reconstruction algorithms have been reported, which dramatically reduce the time complexity than iterative reconstruction algorithms. In this paper, we propose a novel \textbf{D}eep \textbf{R}esidual \textbf{R}econstruction Network (DR$^{2}$-Net) to reconstruct the image from its Compressively Sensed (CS) measurement. The DR$^{2}$-Net is proposed based on two observations: 1) linear mapping could reconstruct a high-quality preliminary image, and 2) residual learning could further improve the reconstruction quality. Accordingly, DR$^{2}$-Net consists of two components, \emph{i.e.,} linear mapping network and residual network, respectively. Specifically, the fully-connected layer in neural network implements the linear mapping network. We then expand the linear mapping network to DR$^{2}$-Net by adding several residual learning blocks to enhance the preliminary image. Extensive experiments demonstrate that the DR$^{2}$-Net outperforms traditional iterative methods and recent deep learning-based methods by large margins at measurement rates 0.01, 0.04, 0.1, and 0.25, respectively. The code of DR$^{2}$-Net has been released on: https://github.com/coldrainyht/caffe\_dr2