Physics-informed 4D X-ray image reconstruction from ultra-sparse spatiotemporal data

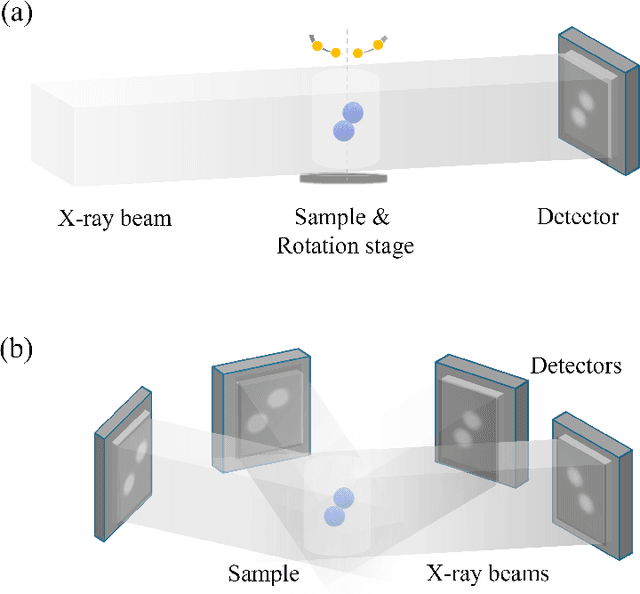
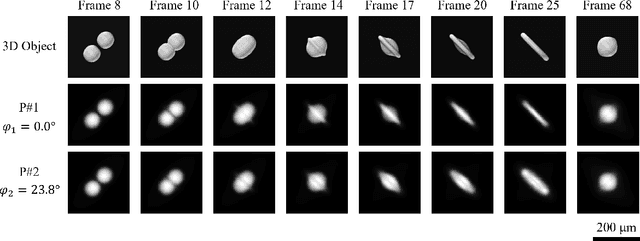
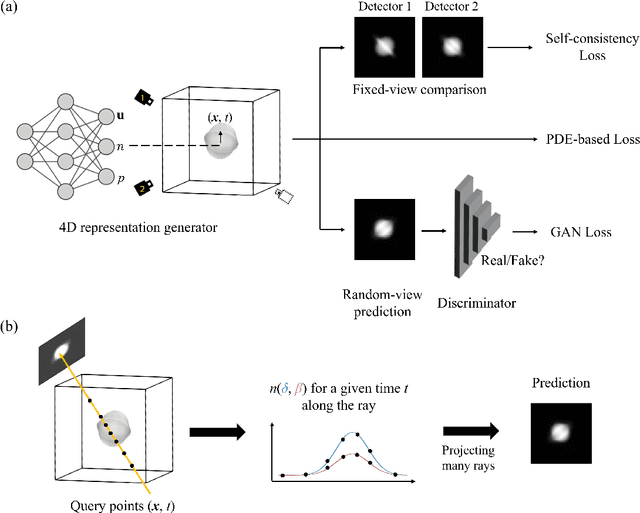
The unprecedented X-ray flux density provided by modern X-ray sources offers new spatiotemporal possibilities for X-ray imaging of fast dynamic processes. Approaches to exploit such possibilities often result in either i) a limited number of projections or spatial information due to limited scanning speed, as in time-resolved tomography, or ii) a limited number of time points, as in stroboscopic imaging, making the reconstruction problem ill-posed and unlikely to be solved by classical reconstruction approaches. 4D reconstruction from such data requires sample priors, which can be included via deep learning (DL). State-of-the-art 4D reconstruction methods for X-ray imaging combine the power of AI and the physics of X-ray propagation to tackle the challenge of sparse views. However, most approaches do not constrain the physics of the studied process, i.e., a full physical model. Here we present 4D physics-informed optimized neural implicit X-ray imaging (4D-PIONIX), a novel physics-informed 4D X-ray image reconstruction method combining the full physical model and a state-of-the-art DL-based reconstruction method for 4D X-ray imaging from sparse views. We demonstrate and evaluate the potential of our approach by retrieving 4D information from ultra-sparse spatiotemporal acquisitions of simulated binary droplet collisions, a relevant fluid dynamic process. We envision that this work will open new spatiotemporal possibilities for various 4D X-ray imaging modalities, such as time-resolved X-ray tomography and more novel sparse acquisition approaches like X-ray multi-projection imaging, which will pave the way for investigations of various rapid 4D dynamics, such as fluid dynamics and composite testing.

Generative Video Bi-flow

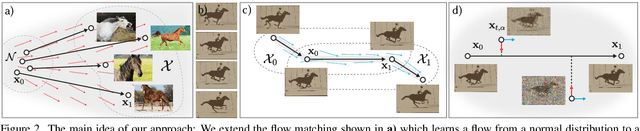
We propose a novel generative video model by robustly learning temporal change as a neural Ordinary Differential Equation (ODE) flow with a bilinear objective of combining two aspects: The first is to map from the past into future video frames directly. Previous work has mapped the noise to new frames, a more computationally expensive process. Unfortunately, starting from the previous frame, instead of noise, is more prone to drifting errors. Hence, second, we additionally learn how to remove the accumulated errors as the joint objective by adding noise during training. We demonstrate unconditional video generation in a streaming manner for various video datasets, all at competitive quality compared to a baseline conditional diffusion but with higher speed, i.e., fewer ODE solver steps.

Blind Augmentation: Calibration-free Camera Distortion Model Estimation for Real-time Mixed-reality Consistency

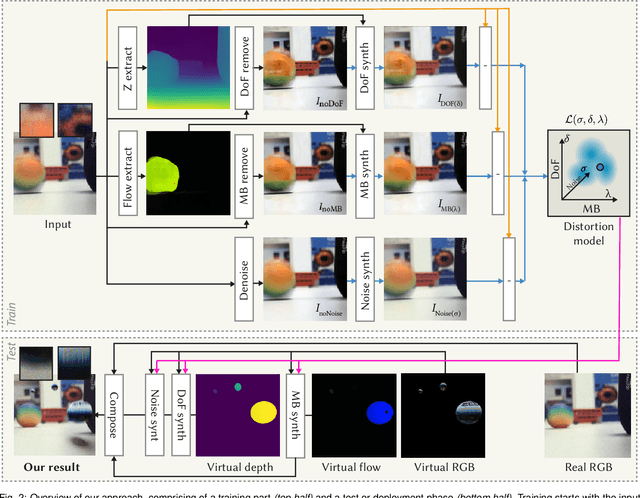
Real camera footage is subject to noise, motion blur (MB) and depth of field (DoF). In some applications these might be considered distortions to be removed, but in others it is important to model them because it would be ineffective, or interfere with an aesthetic choice, to simply remove them. In augmented reality applications where virtual content is composed into a live video feed, we can model noise, MB and DoF to make the virtual content visually consistent with the video. Existing methods for this typically suffer two main limitations. First, they require a camera calibration step to relate a known calibration target to the specific cameras response. Second, existing work require methods that can be (differentiably) tuned to the calibration, such as slow and specialized neural networks. We propose a method which estimates parameters for noise, MB and DoF instantly, which allows using off-the-shelf real-time simulation methods from e.g., a game engine in compositing augmented content. Our main idea is to unlock both features by showing how to use modern computer vision methods that can remove noise, MB and DoF from the video stream, essentially providing self-calibration. This allows to auto-tune any black-box real-time noise+MB+DoF method to deliver fast and high-fidelity augmentation consistency.

SAMa: Material-aware 3D Selection and Segmentation

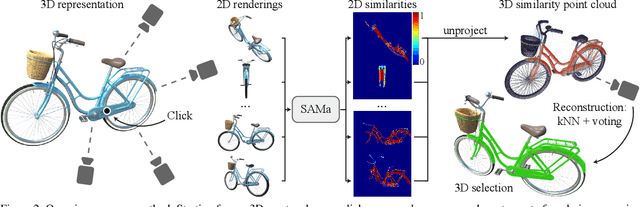
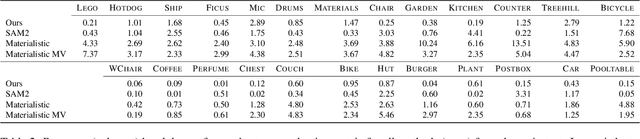
Decomposing 3D assets into material parts is a common task for artists and creators, yet remains a highly manual process. In this work, we introduce Select Any Material (SAMa), a material selection approach for various 3D representations. Building on the recently introduced SAM2 video selection model, we extend its capabilities to the material domain. We leverage the model's cross-view consistency to create a 3D-consistent intermediate material-similarity representation in the form of a point cloud from a sparse set of views. Nearest-neighbour lookups in this similarity cloud allow us to efficiently reconstruct accurate continuous selection masks over objects' surfaces that can be inspected from any view. Our method is multiview-consistent by design, alleviating the need for contrastive learning or feature-field pre-processing, and performs optimization-free selection in seconds. Our approach works on arbitrary 3D representations and outperforms several strong baselines in terms of selection accuracy and multiview consistency. It enables several compelling applications, such as replacing the diffuse-textured materials on a text-to-3D output, or selecting and editing materials on NeRFs and 3D-Gaussians.

Exposure Diffusion: HDR Image Generation by Consistent LDR denoising

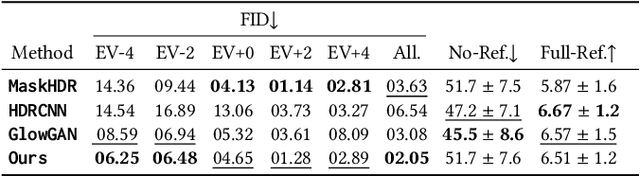
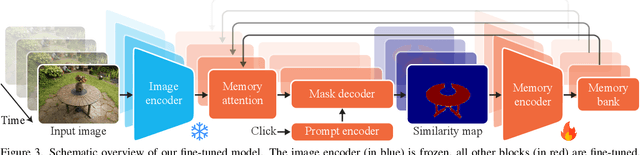
We demonstrate generating high-dynamic range (HDR) images using the concerted action of multiple black-box, pre-trained low-dynamic range (LDR) image diffusion models. Common diffusion models are not HDR as, first, there is no sufficiently large HDR image dataset available to re-train them, and second, even if it was, re-training such models is impossible for most compute budgets. Instead, we seek inspiration from the HDR image capture literature that traditionally fuses sets of LDR images, called "brackets", to produce a single HDR image. We operate multiple denoising processes to generate multiple LDR brackets that together form a valid HDR result. To this end, we introduce an exposure consistency term into the diffusion process to couple the brackets such that they agree across the exposure range they share. We demonstrate HDR versions of state-of-the-art unconditional and conditional as well as restoration-type (LDR2HDR) generative modeling.

NeRF Analogies: Example-Based Visual Attribute Transfer for NeRFs

A Neural Radiance Field (NeRF) encodes the specific relation of 3D geometry and appearance of a scene. We here ask the question whether we can transfer the appearance from a source NeRF onto a target 3D geometry in a semantically meaningful way, such that the resulting new NeRF retains the target geometry but has an appearance that is an analogy to the source NeRF. To this end, we generalize classic image analogies from 2D images to NeRFs. We leverage correspondence transfer along semantic affinity that is driven by semantic features from large, pre-trained 2D image models to achieve multi-view consistent appearance transfer. Our method allows exploring the mix-and-match product space of 3D geometry and appearance. We show that our method outperforms traditional stylization-based methods and that a large majority of users prefer our method over several typical baselines.

4D-ONIX: A deep learning approach for reconstructing 3D movies from sparse X-ray projections

The X-ray flux provided by X-ray free-electron lasers and storage rings offers new spatiotemporal possibilities to study in-situ and operando dynamics, even using single pulses of such facilities. X-ray Multi-Projection Imaging (XMPI) is a novel technique that enables volumetric information using single pulses of such facilities and avoids centrifugal forces induced by state-of-the-art time-resolved 3D methods such as time-resolved tomography. As a result, XMPI can acquire 3D movies (4D) at least three orders of magnitude faster than current methods. However, it is exceptionally challenging to reconstruct 4D from highly sparse projections as acquired by XMPI with current algorithms. Here, we present 4D-ONIX, a Deep Learning (DL)-based approach that learns to reconstruct 3D movies (4D) from an extremely limited number of projections. It combines the computational physical model of X-ray interaction with matter and state-of-the-art DL methods. We demonstrate the potential of 4D-ONIX to generate high-quality 4D by generalizing over multiple experiments with only two projections per timestamp for binary droplet collisions. We envision that 4D-ONIX will become an enabling tool for 4D analysis, offering new spatiotemporal resolutions to study processes not possible before.

Neural Bounding

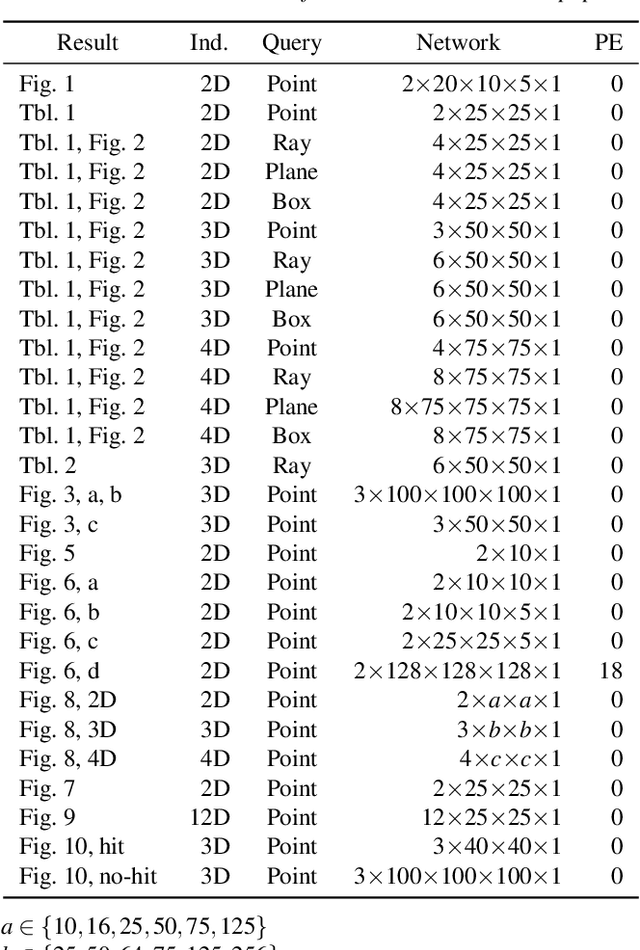
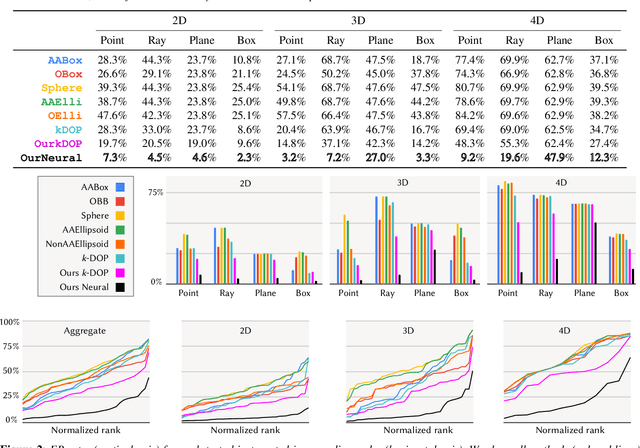
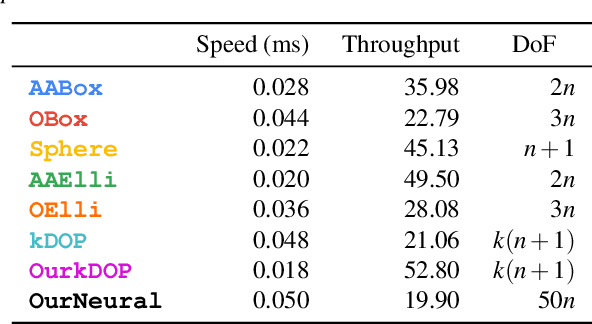
Bounding volumes are an established concept in computer graphics and vision tasks but have seen little change since their early inception. In this work, we study the use of neural networks as bounding volumes. Our key observation is that bounding, which so far has primarily been considered a problem of computational geometry, can be redefined as a problem of learning to classify space into free and empty. This learning-based approach is particularly advantageous in high-dimensional spaces, such as animated scenes with complex queries, where neural networks are known to excel. However, unlocking neural bounding requires a twist: allowing -- but also limiting -- false positives, while ensuring that the number of false negatives is strictly zero. We enable such tight and conservative results using a dynamically-weighted asymmetric loss function. Our results show that our neural bounding produces up to an order of magnitude fewer false positives than traditional methods.

Zero Grads Ever Given: Learning Local Surrogate Losses for Non-Differentiable Graphics

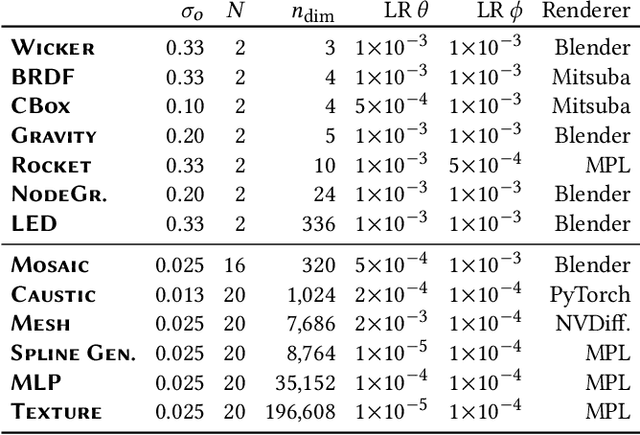
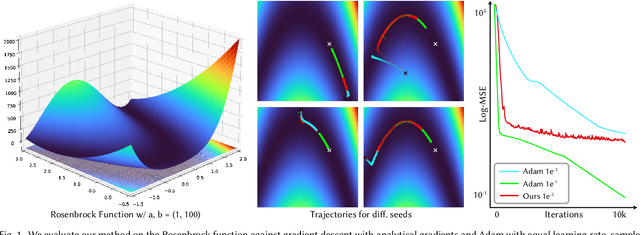
Gradient-based optimization is now ubiquitous across graphics, but unfortunately can not be applied to problems with undefined or zero gradients. To circumvent this issue, the loss function can be manually replaced by a "surrogate" that has similar minima but is differentiable. Our proposed framework, ZeroGrads, automates this process by learning a neural approximation of the objective function, the surrogate, which in turn can be used to differentiate through arbitrary black-box graphics pipelines. We train the surrogate on an actively smoothed version of the objective and encourage locality, focusing the surrogate's capacity on what matters at the current training episode. The fitting is performed online, alongside the parameter optimization, and self-supervised, without pre-computed data or pre-trained models. As sampling the objective is expensive (it requires a full rendering or simulator run), we devise an efficient sampling scheme that allows for tractable run-times and competitive performance at little overhead. We demonstrate optimizing diverse non-convex, non-differentiable black-box problems in graphics, such as visibility in rendering, discrete parameter spaces in procedural modelling or optimal control in physics-driven animation. In contrast to more traditional algorithms, our approach scales well to higher dimensions, which we demonstrate on problems with up to 35k interlinked variables.

Megahertz X-ray Multi-projection imaging

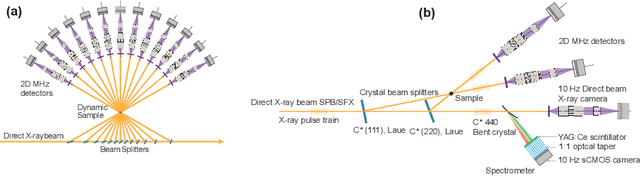
X-ray time-resolved tomography is one of the most popular X-ray techniques to probe dynamics in three dimensions (3D). Recent developments in time-resolved tomography opened the possibility of recording kilohertz-rate 3D movies. However, tomography requires rotating the sample with respect to the X-ray beam, which prevents characterization of faster structural dynamics. Here, we present megahertz (MHz) X-ray multi-projection imaging (MHz-XMPI), a technique capable of recording volumetric information at MHz rates and micrometer resolution without scanning the sample. We achieved this by harnessing the unique megahertz pulse structure and intensity of the European X-ray Free-electron Laser with a combination of novel detection and reconstruction approaches that do not require sample rotations. Our approach enables generating multiple X-ray probes that simultaneously record several angular projections for each pulse in the megahertz pulse burst. We provide a proof-of-concept demonstration of the MHz-XMPI technique's capability to probe 4D (3D+time) information on stochastic phenomena and non-reproducible processes three orders of magnitude faster than state-of-the-art time-resolved X-ray tomography, by generating 3D movies of binary droplet collisions. We anticipate that MHz-XMPI will enable in-situ and operando studies that were impossible before, either due to the lack of temporal resolution or because the systems were opaque (such as for MHz imaging based on optical microscopy).