Neural Bounding
Paper and Code
Oct 10, 2023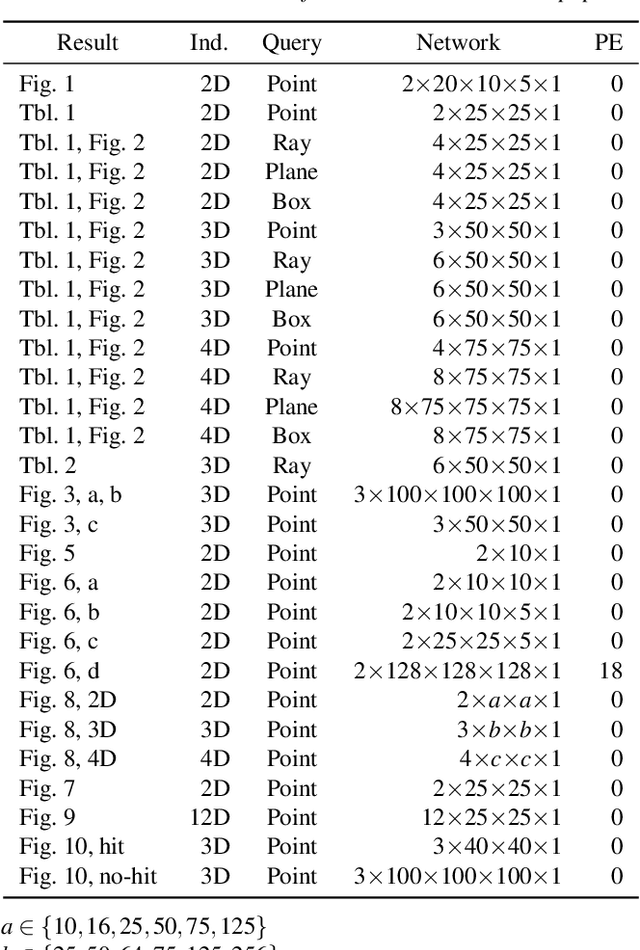
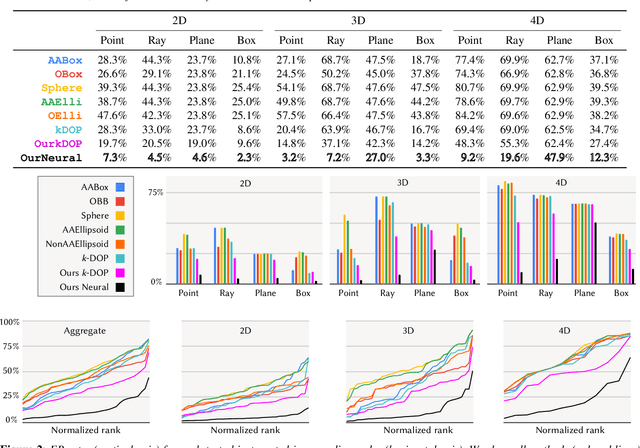
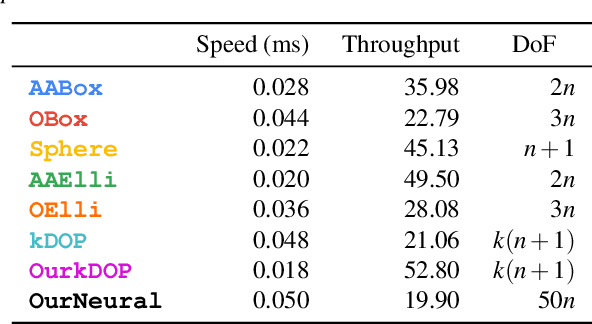

Bounding volumes are an established concept in computer graphics and vision tasks but have seen little change since their early inception. In this work, we study the use of neural networks as bounding volumes. Our key observation is that bounding, which so far has primarily been considered a problem of computational geometry, can be redefined as a problem of learning to classify space into free and empty. This learning-based approach is particularly advantageous in high-dimensional spaces, such as animated scenes with complex queries, where neural networks are known to excel. However, unlocking neural bounding requires a twist: allowing -- but also limiting -- false positives, while ensuring that the number of false negatives is strictly zero. We enable such tight and conservative results using a dynamically-weighted asymmetric loss function. Our results show that our neural bounding produces up to an order of magnitude fewer false positives than traditional methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge