Vision Technologies with Applications in Traffic Surveillance Systems: A Holistic Survey

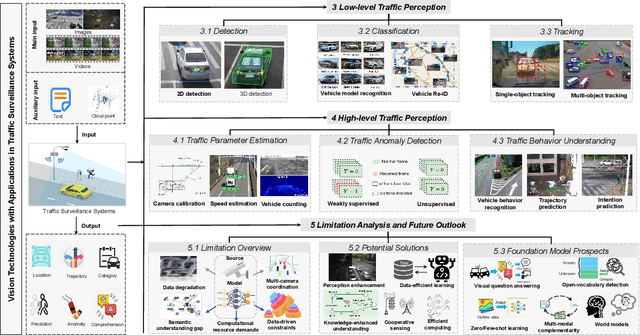
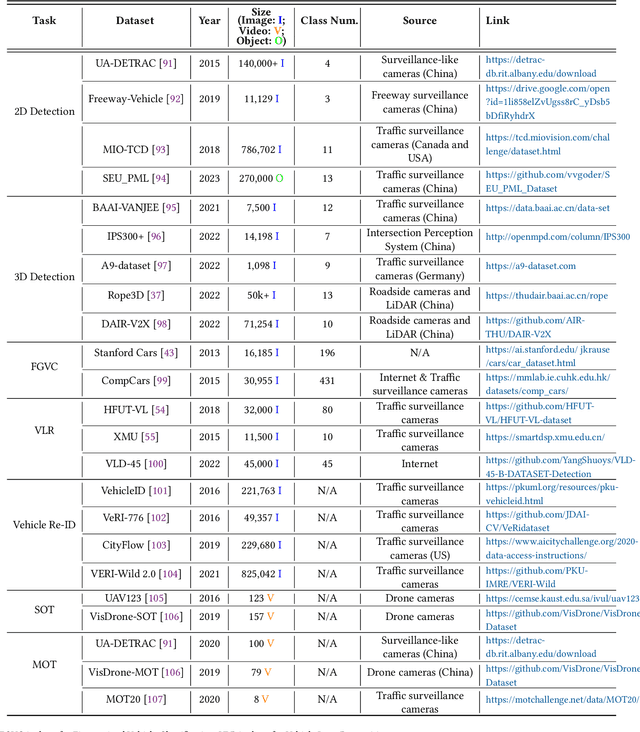
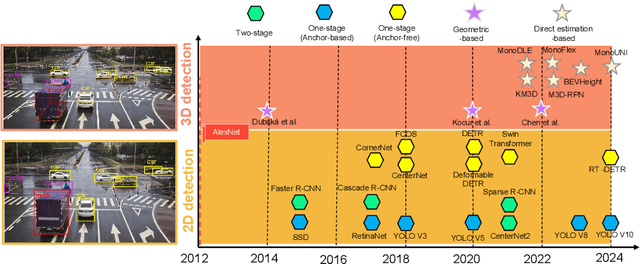
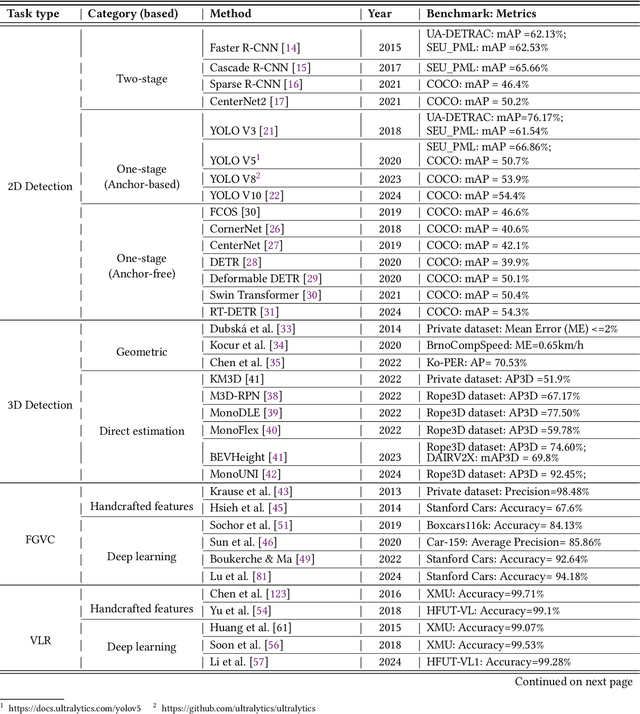
Traffic Surveillance Systems (TSS) have become increasingly crucial in modern intelligent transportation systems, with vision-based technologies playing a central role for scene perception and understanding. While existing surveys typically focus on isolated aspects of TSS, a comprehensive analysis bridging low-level and high-level perception tasks, particularly considering emerging technologies, remains lacking. This paper presents a systematic review of vision-based technologies in TSS, examining both low-level perception tasks (object detection, classification, and tracking) and high-level perception applications (parameter estimation, anomaly detection, and behavior understanding). Specifically, we first provide a detailed methodological categorization and comprehensive performance evaluation for each task. Our investigation reveals five fundamental limitations in current TSS: perceptual data degradation in complex scenarios, data-driven learning constraints, semantic understanding gaps, sensing coverage limitations and computational resource demands. To address these challenges, we systematically analyze five categories of potential solutions: advanced perception enhancement, efficient learning paradigms, knowledge-enhanced understanding, cooperative sensing frameworks and efficient computing frameworks. Furthermore, we evaluate the transformative potential of foundation models in TSS, demonstrating their unique capabilities in zero-shot learning, semantic understanding, and scene generation. This review provides a unified framework bridging low-level and high-level perception tasks, systematically analyzes current limitations and solutions, and presents a structured roadmap for integrating emerging technologies, particularly foundation models, to enhance TSS capabilities.

Cooperative Multi-Agent Graph Bandits: UCB Algorithm and Regret Analysis

In this paper, we formulate the multi-agent graph bandit problem as a multi-agent extension of the graph bandit problem introduced by Zhang, Johansson, and Li [CISS 57, 1-6 (2023)]. In our formulation, $N$ cooperative agents travel on a connected graph $G$ with $K$ nodes. Upon arrival at each node, agents observe a random reward drawn from a node-dependent probability distribution. The reward of the system is modeled as a weighted sum of the rewards the agents observe, where the weights capture the decreasing marginal reward associated with multiple agents sampling the same node at the same time. We propose an Upper Confidence Bound (UCB)-based learning algorithm, Multi-G-UCB, and prove that its expected regret over $T$ steps is bounded by $O(N\log(T)[\sqrt{KT} + DK])$, where $D$ is the diameter of graph $G$. Lastly, we numerically test our algorithm by comparing it to alternative methods.

Regularized Robust MDPs and Risk-Sensitive MDPs: Equivalence, Policy Gradient, and Sample Complexity

This paper focuses on reinforcement learning for the regularized robust Markov decision process (MDP) problem, an extension of the robust MDP framework. We first introduce the risk-sensitive MDP and establish the equivalence between risk-sensitive MDP and regularized robust MDP. This equivalence offers an alternative perspective for addressing the regularized RMDP and enables the design of efficient learning algorithms. Given this equivalence, we further derive the policy gradient theorem for the regularized robust MDP problem and prove the global convergence of the exact policy gradient method under the tabular setting with direct parameterization. We also propose a sample-based offline learning algorithm, namely the robust fitted-Z iteration (RFZI), for a specific regularized robust MDP problem with a KL-divergence regularization term and analyze the sample complexity of the algorithm. Our results are also supported by numerical simulations.

Neural Nonnegative Matrix Factorization for Hierarchical Multilayer Topic Modeling

We introduce a new method based on nonnegative matrix factorization, Neural NMF, for detecting latent hierarchical structure in data. Datasets with hierarchical structure arise in a wide variety of fields, such as document classification, image processing, and bioinformatics. Neural NMF recursively applies NMF in layers to discover overarching topics encompassing the lower-level features. We derive a backpropagation optimization scheme that allows us to frame hierarchical NMF as a neural network. We test Neural NMF on a synthetic hierarchical dataset, the 20 Newsgroups dataset, and the MyLymeData symptoms dataset. Numerical results demonstrate that Neural NMF outperforms other hierarchical NMF methods on these data sets and offers better learned hierarchical structure and interpretability of topics.

Policy Optimization for Markov Games: Unified Framework and Faster Convergence

This paper studies policy optimization algorithms for multi-agent reinforcement learning. We begin by proposing an algorithm framework for two-player zero-sum Markov Games in the full-information setting, where each iteration consists of a policy update step at each state using a certain matrix game algorithm, and a value update step with a certain learning rate. This framework unifies many existing and new policy optimization algorithms. We show that the state-wise average policy of this algorithm converges to an approximate Nash equilibrium (NE) of the game, as long as the matrix game algorithms achieve low weighted regret at each state, with respect to weights determined by the speed of the value updates. Next, we show that this framework instantiated with the Optimistic Follow-The-Regularized-Leader (OFTRL) algorithm at each state (and smooth value updates) can find an $\mathcal{\widetilde{O}}(T^{-5/6})$ approximate NE in $T$ iterations, which improves over the current best $\mathcal{\widetilde{O}}(T^{-1/2})$ rate of symmetric policy optimization type algorithms. We also extend this algorithm to multi-player general-sum Markov Games and show an $\mathcal{\widetilde{O}}(T^{-3/4})$ convergence rate to Coarse Correlated Equilibria (CCE). Finally, we provide a numerical example to verify our theory and investigate the importance of smooth value updates, and find that using "eager" value updates instead (equivalent to the independent natural policy gradient algorithm) may significantly slow down the convergence, even on a simple game with $H=2$ layers.

Gradient Play in Multi-Agent Markov Stochastic Games: Stationary Points and Convergence

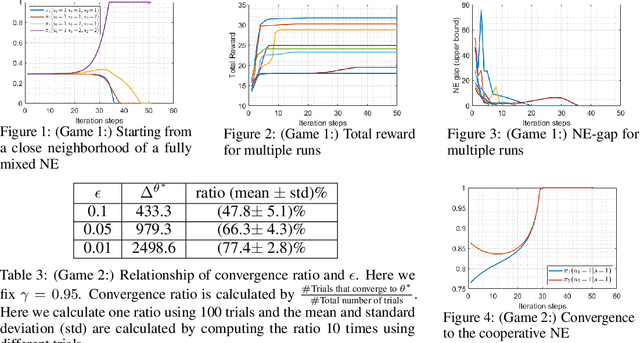
We study the performance of the gradient play algorithm for multi-agent tabular Markov decision processes (MDPs), which are also known as stochastic games (SGs), where each agent tries to maximize its own total discounted reward by making decisions independently based on current state information which is shared between agents. Policies are directly parameterized by the probability of choosing a certain action at a given state. We show that Nash equilibria (NEs) and first order stationary policies are equivalent in this setting, and give a non-asymptotic global convergence rate analysis to an $\epsilon$-NE for a subclass of multi-agent MDPs called Markov potential games, which includes the cooperative setting with identical rewards among agents as an important special case. Our result shows that the number of iterations to reach an $\epsilon$-NE scales linearly, instead of exponentially, with the number of agents. Local geometry and local stability are also considered. For Markov potential games, we prove that strict NEs are local maxima of the total potential function and fully-mixed NEs are saddle points. We also give a local convergence rate around strict NEs for more general settings.

Distributed Reinforcement Learning for Decentralized Linear Quadratic Control: A Derivative-Free Policy Optimization Approach

This paper considers a distributed reinforcement learning problem for decentralized linear quadratic control with partial state observations and local costs. We propose the Zero-Order Distributed Policy Optimization algorithm (ZODPO) that learns linear local controllers in a distributed fashion, leveraging the ideas of policy gradient, zero-order optimization and consensus algorithms. In ZODPO, each agent estimates the global cost by consensus, and then conducts local policy gradient in parallel based on zero-order gradient estimation. ZODPO only requires limited communication and storage even in large-scale systems. Further, we investigate the nonasymptotic performance of ZODPO and show that the sample complexity to approach a stationary point is polynomial with the error tolerance's inverse and the problem dimensions, demonstrating the scalability of ZODPO. We also show that the controllers generated by ZODPO are stabilizing with high probability. Lastly, we numerically test ZODPO on a multi-zone HVAC system.