Neural Nonnegative Matrix Factorization for Hierarchical Multilayer Topic Modeling

We introduce a new method based on nonnegative matrix factorization, Neural NMF, for detecting latent hierarchical structure in data. Datasets with hierarchical structure arise in a wide variety of fields, such as document classification, image processing, and bioinformatics. Neural NMF recursively applies NMF in layers to discover overarching topics encompassing the lower-level features. We derive a backpropagation optimization scheme that allows us to frame hierarchical NMF as a neural network. We test Neural NMF on a synthetic hierarchical dataset, the 20 Newsgroups dataset, and the MyLymeData symptoms dataset. Numerical results demonstrate that Neural NMF outperforms other hierarchical NMF methods on these data sets and offers better learned hierarchical structure and interpretability of topics.

Joint NMF for Identification of Shared Features in Datasets and a Dataset Distance Measure

In this paper, we derive a new method for determining shared features of datasets by employing joint non-negative matrix factorization and analyzing the resulting factorizations. Our approach uses the joint factorization of two dataset matrices $X_1,X_2$ into non-negative matrices $X_1 = AS_1, X_2 = AS_2$ to derive a similarity measure that determines how well a shared basis for $X_1, X_2$ approximates each dataset. We also propose a dataset distance measure built upon this method and the learned factorization. Our method is able to successfully identity differences in structure in both image and text datasets. Potential applications include classification, detecting plagiarism or other manipulation, and learning relationships between data sets.

Nonbacktracking spectral clustering of nonuniform hypergraphs

Spectral methods offer a tractable, global framework for clustering in graphs via eigenvector computations on graph matrices. Hypergraph data, in which entities interact on edges of arbitrary size, poses challenges for matrix representations and therefore for spectral clustering. We study spectral clustering for nonuniform hypergraphs based on the hypergraph nonbacktracking operator. After reviewing the definition of this operator and its basic properties, we prove a theorem of Ihara-Bass type to enable faster computation of eigenpairs. We then propose an alternating algorithm for inference in a hypergraph stochastic blockmodel via linearized belief-propagation, offering proofs that both formalize and extend several previous results. We perform experiments in real and synthetic data that underscore the benefits of hypergraph methods over graph-based ones when interactions of different sizes carry different information about cluster structure. Through an analysis of our algorithm, we pose several conjectures about the limits of spectral methods and detectability in hypergraph stochastic blockmodels writ large.

Semi-supervised Nonnegative Matrix Factorization for Document Classification

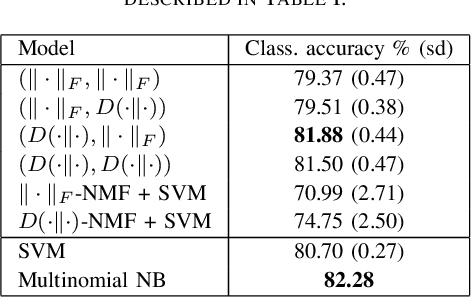
We propose new semi-supervised nonnegative matrix factorization (SSNMF) models for document classification and provide motivation for these models as maximum likelihood estimators. The proposed SSNMF models simultaneously provide both a topic model and a model for classification, thereby offering highly interpretable classification results. We derive training methods using multiplicative updates for each new model, and demonstrate the application of these models to single-label and multi-label document classification, although the models are flexible to other supervised learning tasks such as regression. We illustrate the promise of these models and training methods on document classification datasets (e.g., 20 Newsgroups, Reuters).

A Generalized Hierarchical Nonnegative Tensor Decomposition

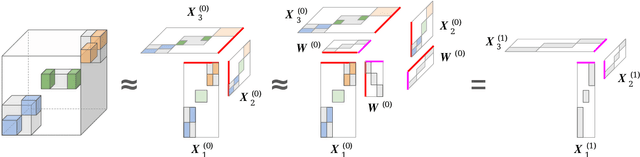
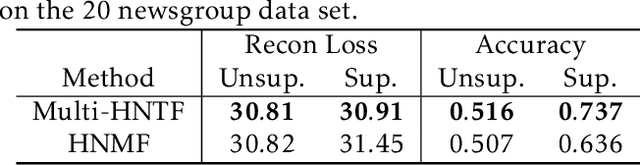
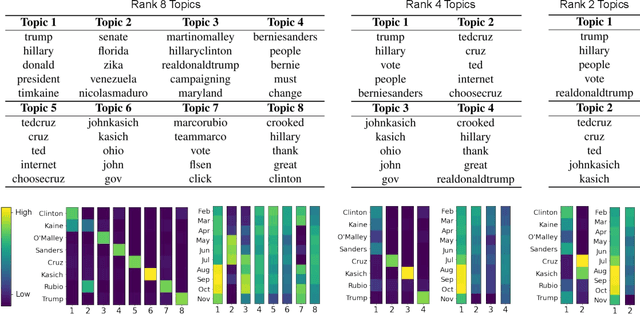
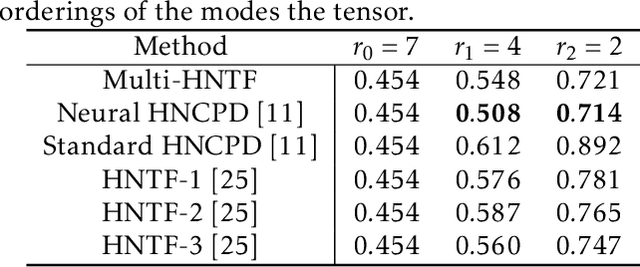
Nonnegative matrix factorization (NMF) has found many applications including topic modeling and document analysis. Hierarchical NMF (HNMF) variants are able to learn topics at various levels of granularity and illustrate their hierarchical relationship. Recently, nonnegative tensor factorization (NTF) methods have been applied in a similar fashion in order to handle data sets with complex, multi-modal structure. Hierarchical NTF (HNTF) methods have been proposed, however these methods do not naturally generalize their matrix-based counterparts. Here, we propose a new HNTF model which directly generalizes a HNMF model special case, and provide a supervised extension. We also provide a multiplicative updates training method for this model. Our experimental results show that this model more naturally illuminates the topic hierarchy than previous HNMF and HNTF methods.

On a Guided Nonnegative Matrix Factorization

Fully unsupervised topic models have found fantastic success in document clustering and classification. However, these models often suffer from the tendency to learn less-than-meaningful or even redundant topics when the data is biased towards a set of features. For this reason, we propose an approach based upon the nonnegative matrix factorization (NMF) model, deemed \textit{Guided NMF}, that incorporates user-designed seed word supervision. Our experimental results demonstrate the promise of this model and illustrate that it is competitive with other methods of this ilk with only very little supervision information.

On Application of Block Kaczmarz Methods in Matrix Factorization

Matrix factorization techniques compute low-rank product approximations of high dimensional data matrices and as a result, are often employed in recommender systems and collaborative filtering applications. However, many algorithms for this task utilize an exact least-squares solver whose computation is time consuming and memory-expensive. In this paper we discuss and test a block Kaczmarz solver that replaces the least-squares subroutine in the common alternating scheme for matrix factorization. This variant trades a small increase in factorization error for significantly faster algorithmic performance. In doing so we find block sizes that produce a solution comparable to that of the least-squares solver for only a fraction of the runtime and working memory requirement.

Semi-supervised NMF Models for Topic Modeling in Learning Tasks

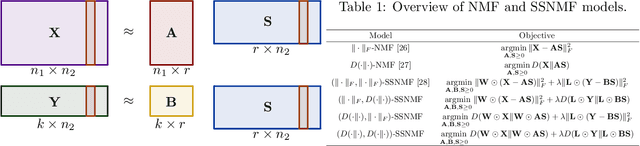
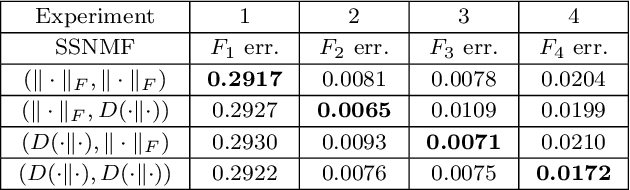
We propose several new models for semi-supervised nonnegative matrix factorization (SSNMF) and provide motivation for SSNMF models as maximum likelihood estimators given specific distributions of uncertainty. We present multiplicative updates training methods for each new model, and demonstrate the application of these models to classification, although they are flexible to other supervised learning tasks. We illustrate the promise of these models and training methods on both synthetic and real data, and achieve high classification accuracy on the 20 Newsgroups dataset.

Feature Selection on Lyme Disease Patient Survey Data

Lyme disease is a rapidly growing illness that remains poorly understood within the medical community. Critical questions about when and why patients respond to treatment or stay ill, what kinds of treatments are effective, and even how to properly diagnose the disease remain largely unanswered. We investigate these questions by applying machine learning techniques to a large scale Lyme disease patient registry, MyLymeData, developed by the nonprofit LymeDisease.org. We apply various machine learning methods in order to measure the effect of individual features in predicting participants' answers to the Global Rating of Change (GROC) survey questions that assess the self-reported degree to which their condition improved, worsened, or remained unchanged following antibiotic treatment. We use basic linear regression, support vector machines, neural networks, entropy-based decision tree models, and $k$-nearest neighbors approaches. We first analyze the general performance of the model and then identify the most important features for predicting participant answers to GROC. After we identify the "key" features, we separate them from the dataset and demonstrate the effectiveness of these features at identifying GROC. In doing so, we highlight possible directions for future study both mathematically and clinically.

On Large-Scale Dynamic Topic Modeling with Nonnegative CP Tensor Decomposition

There is currently an unprecedented demand for large-scale temporal data analysis due to the explosive growth of data. Dynamic topic modeling has been widely used in social and data sciences with the goal of learning latent topics that emerge, evolve, and fade over time. Previous work on dynamic topic modeling primarily employ the method of nonnegative matrix factorization (NMF), where slices of the data tensor are each factorized into the product of lower-dimensional nonnegative matrices. With this approach, however, information contained in the temporal dimension of the data is often neglected or underutilized. To overcome this issue, we propose instead adopting the method of nonnegative CANDECOMP/PARAPAC (CP) tensor decomposition (NNCPD), where the data tensor is directly decomposed into a minimal sum of outer products of nonnegative vectors, thereby preserving the temporal information. The viability of NNCPD is demonstrated through application to both synthetic and real data, where significantly improved results are obtained compared to those of typical NMF-based methods. The advantages of NNCPD over such approaches are studied and discussed. To the best of our knowledge, this is the first time that NNCPD has been utilized for the purpose of dynamic topic modeling, and our findings will be transformative for both applications and further developments.