Rachel Grotheer
Stochastic Natural Thresholding Algorithms
Jun 07, 2023Abstract:Sparse signal recovery is one of the most fundamental problems in various applications, including medical imaging and remote sensing. Many greedy algorithms based on the family of hard thresholding operators have been developed to solve the sparse signal recovery problem. More recently, Natural Thresholding (NT) has been proposed with improved computational efficiency. This paper proposes and discusses convergence guarantees for stochastic natural thresholding algorithms by extending the NT from the deterministic version with linear measurements to the stochastic version with a general objective function. We also conduct various numerical experiments on linear and nonlinear measurements to demonstrate the performance of StoNT.
Semi-supervised Nonnegative Matrix Factorization for Document Classification
Feb 28, 2022

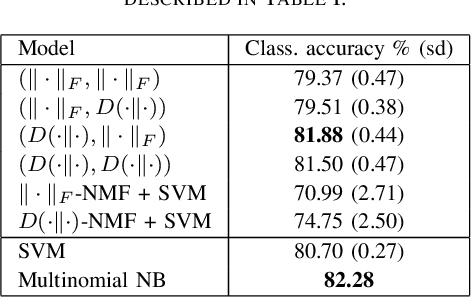

Abstract:We propose new semi-supervised nonnegative matrix factorization (SSNMF) models for document classification and provide motivation for these models as maximum likelihood estimators. The proposed SSNMF models simultaneously provide both a topic model and a model for classification, thereby offering highly interpretable classification results. We derive training methods using multiplicative updates for each new model, and demonstrate the application of these models to single-label and multi-label document classification, although the models are flexible to other supervised learning tasks such as regression. We illustrate the promise of these models and training methods on document classification datasets (e.g., 20 Newsgroups, Reuters).
Semi-supervised NMF Models for Topic Modeling in Learning Tasks
Oct 15, 2020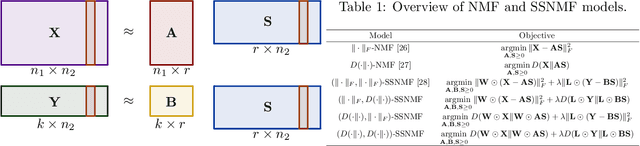
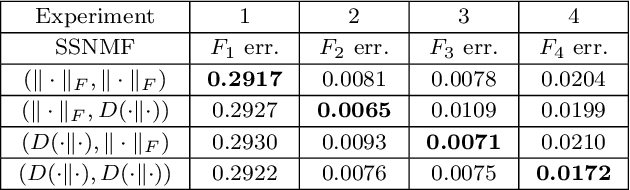


Abstract:We propose several new models for semi-supervised nonnegative matrix factorization (SSNMF) and provide motivation for SSNMF models as maximum likelihood estimators given specific distributions of uncertainty. We present multiplicative updates training methods for each new model, and demonstrate the application of these models to classification, although they are flexible to other supervised learning tasks. We illustrate the promise of these models and training methods on both synthetic and real data, and achieve high classification accuracy on the 20 Newsgroups dataset.
COVID-19 Literature Topic-Based Search via Hierarchical NMF
Sep 07, 2020



Abstract:A dataset of COVID-19-related scientific literature is compiled, combining the articles from several online libraries and selecting those with open access and full text available. Then, hierarchical nonnegative matrix factorization is used to organize literature related to the novel coronavirus into a tree structure that allows researchers to search for relevant literature based on detected topics. We discover eight major latent topics and 52 granular subtopics in the body of literature, related to vaccines, genetic structure and modeling of the disease and patient studies, as well as related diseases and virology. In order that our tool may help current researchers, an interactive website is created that organizes available literature using this hierarchical structure.
Iterative Hard Thresholding for Low CP-rank Tensor Models
Aug 22, 2019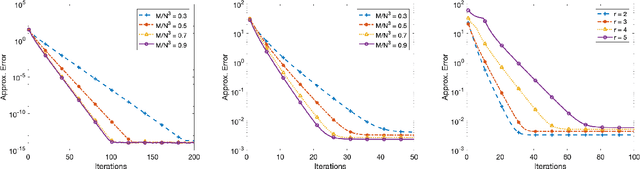
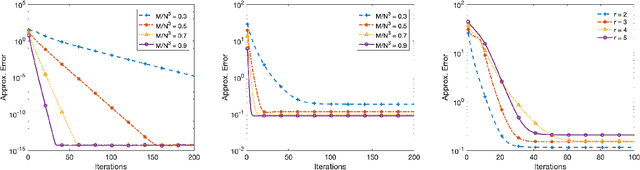
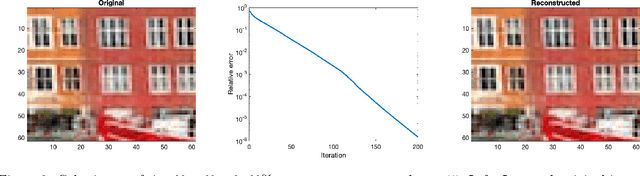
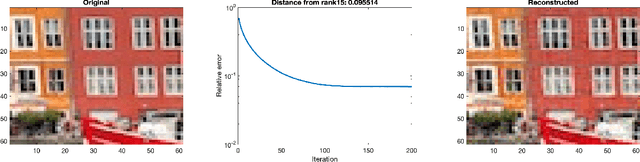
Abstract:Recovery of low-rank matrices from a small number of linear measurements is now well-known to be possible under various model assumptions on the measurements. Such results demonstrate robustness and are backed with provable theoretical guarantees. However, extensions to tensor recovery have only recently began to be studied and developed, despite an abundance of practical tensor applications. Recently, a tensor variant of the Iterative Hard Thresholding method was proposed and theoretical results were obtained that guarantee exact recovery of tensors with low Tucker rank. In this paper, we utilize the same tensor version of the Restricted Isometry Property (RIP) to extend these results for tensors with low CANDECOMP/PARAFAC (CP) rank. In doing so, we leverage recent results on efficient approximations of CP decompositions that remove the need for challenging assumptions in prior works. We complement our theoretical findings with empirical results that showcase the potential of the approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge