Semi-supervised Nonnegative Matrix Factorization for Document Classification

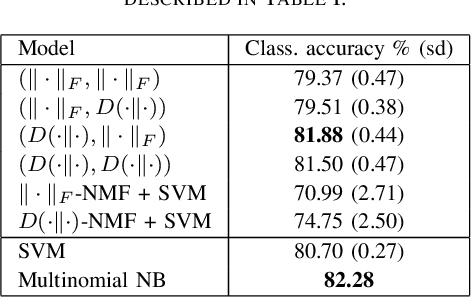
We propose new semi-supervised nonnegative matrix factorization (SSNMF) models for document classification and provide motivation for these models as maximum likelihood estimators. The proposed SSNMF models simultaneously provide both a topic model and a model for classification, thereby offering highly interpretable classification results. We derive training methods using multiplicative updates for each new model, and demonstrate the application of these models to single-label and multi-label document classification, although the models are flexible to other supervised learning tasks such as regression. We illustrate the promise of these models and training methods on document classification datasets (e.g., 20 Newsgroups, Reuters).

Semi-supervised NMF Models for Topic Modeling in Learning Tasks

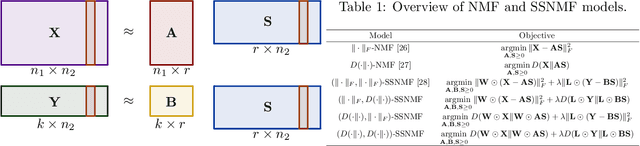
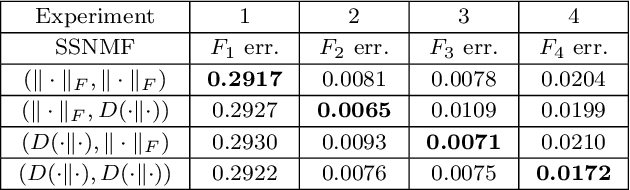
We propose several new models for semi-supervised nonnegative matrix factorization (SSNMF) and provide motivation for SSNMF models as maximum likelihood estimators given specific distributions of uncertainty. We present multiplicative updates training methods for each new model, and demonstrate the application of these models to classification, although they are flexible to other supervised learning tasks. We illustrate the promise of these models and training methods on both synthetic and real data, and achieve high classification accuracy on the 20 Newsgroups dataset.

COVID-19 Literature Topic-Based Search via Hierarchical NMF

A dataset of COVID-19-related scientific literature is compiled, combining the articles from several online libraries and selecting those with open access and full text available. Then, hierarchical nonnegative matrix factorization is used to organize literature related to the novel coronavirus into a tree structure that allows researchers to search for relevant literature based on detected topics. We discover eight major latent topics and 52 granular subtopics in the body of literature, related to vaccines, genetic structure and modeling of the disease and patient studies, as well as related diseases and virology. In order that our tool may help current researchers, an interactive website is created that organizes available literature using this hierarchical structure.

On Large-Scale Dynamic Topic Modeling with Nonnegative CP Tensor Decomposition

There is currently an unprecedented demand for large-scale temporal data analysis due to the explosive growth of data. Dynamic topic modeling has been widely used in social and data sciences with the goal of learning latent topics that emerge, evolve, and fade over time. Previous work on dynamic topic modeling primarily employ the method of nonnegative matrix factorization (NMF), where slices of the data tensor are each factorized into the product of lower-dimensional nonnegative matrices. With this approach, however, information contained in the temporal dimension of the data is often neglected or underutilized. To overcome this issue, we propose instead adopting the method of nonnegative CANDECOMP/PARAPAC (CP) tensor decomposition (NNCPD), where the data tensor is directly decomposed into a minimal sum of outer products of nonnegative vectors, thereby preserving the temporal information. The viability of NNCPD is demonstrated through application to both synthetic and real data, where significantly improved results are obtained compared to those of typical NMF-based methods. The advantages of NNCPD over such approaches are studied and discussed. To the best of our knowledge, this is the first time that NNCPD has been utilized for the purpose of dynamic topic modeling, and our findings will be transformative for both applications and further developments.