MagR: Weight Magnitude Reduction for Enhancing Post-Training Quantization

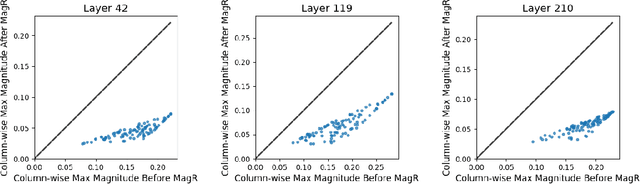
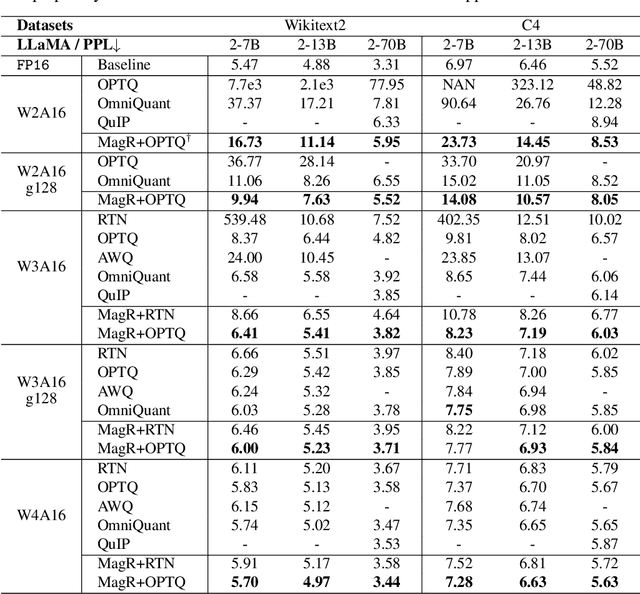
In this paper, we present a simple optimization-based preprocessing technique called Weight Magnitude Reduction (MagR) to improve the performance of post-training quantization. For each linear layer, we adjust the pre-trained floating-point weights by solving an $\ell_\infty$-regularized optimization problem. This process greatly diminishes the maximum magnitude of the weights and smooths out outliers, while preserving the layer's output. The preprocessed weights are centered more towards zero, which facilitates the subsequent quantization process. To implement MagR, we address the $\ell_\infty$-regularization by employing an efficient proximal gradient descent algorithm. Unlike existing preprocessing methods that involve linear transformations and subsequent post-processing steps, which can introduce significant overhead at inference time, MagR functions as a non-linear transformation, eliminating the need for any additional post-processing. This ensures that MagR introduces no overhead whatsoever during inference. Our experiments demonstrate that MagR achieves state-of-the-art performance on the Llama family of models. For example, we achieve a Wikitext2 perplexity of 5.95 on the LLaMA2-70B model for per-channel INT2 weight quantization without incurring any inference overhead.

COMQ: A Backpropagation-Free Algorithm for Post-Training Quantization

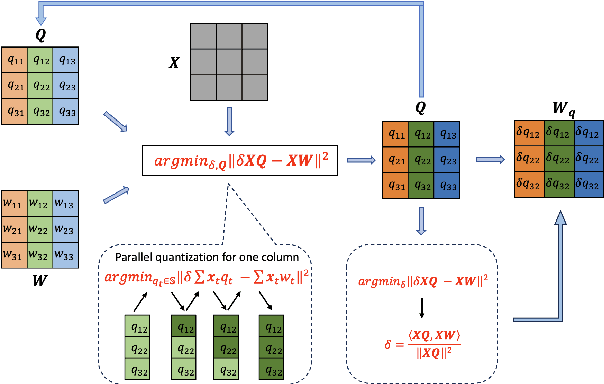
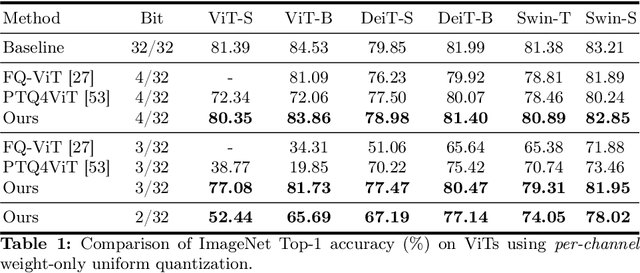
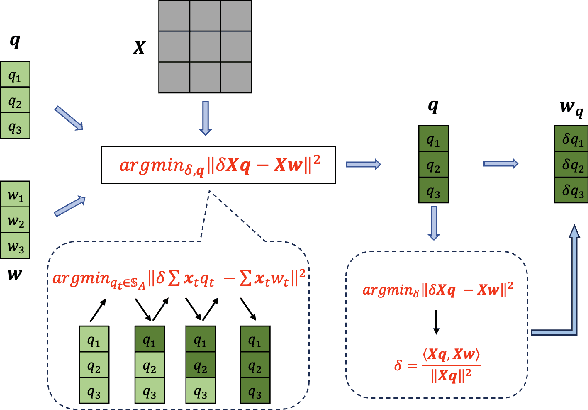
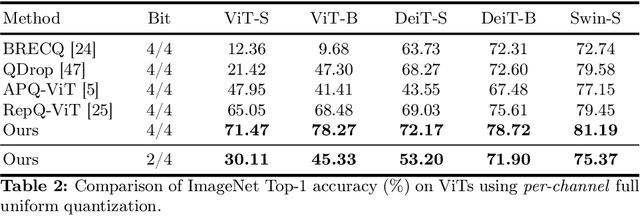
Post-training quantization (PTQ) has emerged as a practical approach to compress large neural networks, making them highly efficient for deployment. However, effectively reducing these models to their low-bit counterparts without compromising the original accuracy remains a key challenge. In this paper, we propose an innovative PTQ algorithm termed COMQ, which sequentially conducts coordinate-wise minimization of the layer-wise reconstruction errors. We consider the widely used integer quantization, where every quantized weight can be decomposed into a shared floating-point scalar and an integer bit-code. Within a fixed layer, COMQ treats all the scaling factor(s) and bit-codes as the variables of the reconstruction error. Every iteration improves this error along a single coordinate while keeping all other variables constant. COMQ is easy to use and requires no hyper-parameter tuning. It instead involves only dot products and rounding operations. We update these variables in a carefully designed greedy order, significantly enhancing the accuracy. COMQ achieves remarkable results in quantizing 4-bit Vision Transformers, with a negligible loss of less than 1% in Top-1 accuracy. In 4-bit INT quantization of convolutional neural networks, COMQ maintains near-lossless accuracy with a minimal drop of merely 0.3% in Top-1 accuracy.

Feature Affinity Assisted Knowledge Distillation and Quantization of Deep Neural Networks on Label-Free Data

In this paper, we propose a feature affinity (FA) assisted knowledge distillation (KD) method to improve quantization-aware training of deep neural networks (DNN). The FA loss on intermediate feature maps of DNNs plays the role of teaching middle steps of a solution to a student instead of only giving final answers in the conventional KD where the loss acts on the network logits at the output level. Combining logit loss and FA loss, we found that the quantized student network receives stronger supervision than from the labeled ground-truth data. The resulting FAQD is capable of compressing model on label-free data, which brings immediate practical benefits as pre-trained teacher models are readily available and unlabeled data are abundant. In contrast, data labeling is often laborious and expensive. Finally, we propose a fast feature affinity (FFA) loss that accurately approximates FA loss with a lower order of computational complexity, which helps speed up training for high resolution image input.

Recurrence of Optimum for Training Weight and Activation Quantized Networks

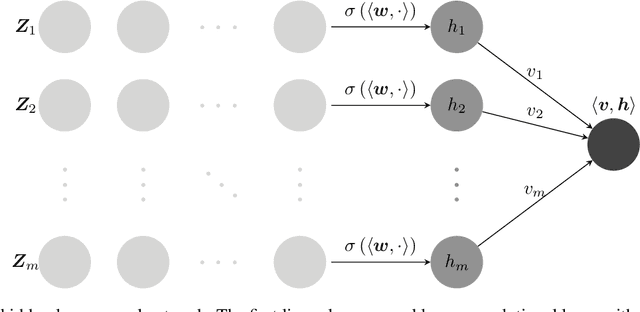
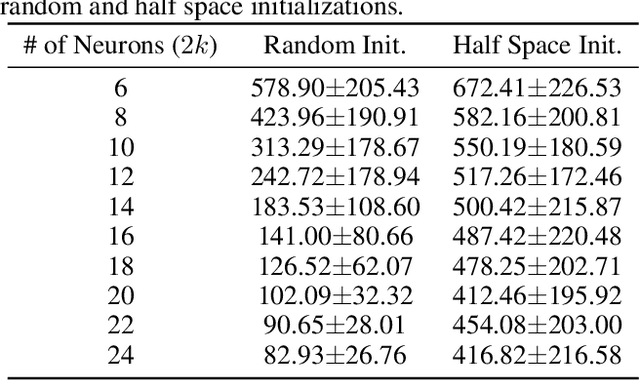
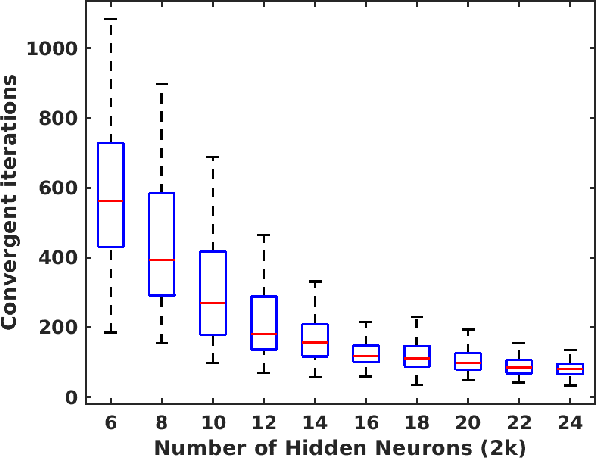
Deep neural networks (DNNs) are quantized for efficient inference on resource-constrained platforms. However, training deep learning models with low-precision weights and activations involves a demanding optimization task, which calls for minimizing a stage-wise loss function subject to a discrete set-constraint. While numerous training methods have been proposed, existing studies for full quantization of DNNs are mostly empirical. From a theoretical point of view, we study practical techniques for overcoming the combinatorial nature of network quantization. Specifically, we investigate a simple yet powerful projected gradient-like algorithm for quantizing two-linear-layer networks, which proceeds by repeatedly moving one step at float weights in the negation of a heuristic \emph{fake} gradient of the loss function (so-called coarse gradient) evaluated at quantized weights. For the first time, we prove that under mild conditions, the sequence of quantized weights recurrently visits the global optimum of the discrete minimization problem for training fully quantized network. We also show numerical evidence of the recurrence phenomenon of weight evolution in training quantized deep networks.

Learning Quantized Neural Nets by Coarse Gradient Method for Non-linear Classification

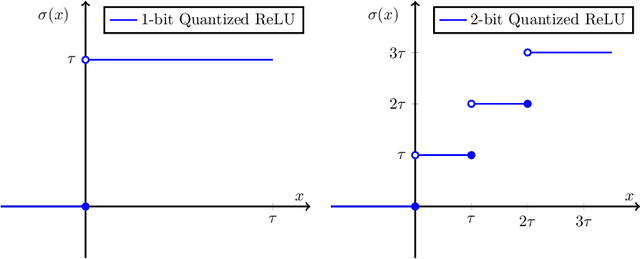
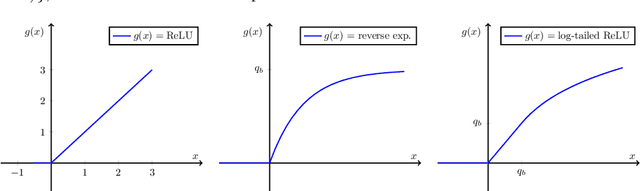
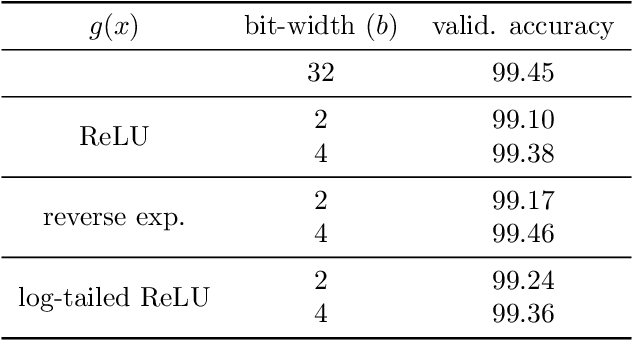
Quantized or low-bit neural networks are attractive due to their inference efficiency. However, training deep neural networks with quantized activations involves minimizing a discontinuous and piecewise constant loss function. Such a loss function has zero gradients almost everywhere (a.e.), which makes the conventional gradient-based algorithms inapplicable. To this end, we study a novel class of \emph{biased} first-order oracle, termed coarse gradient, for overcoming the vanished gradient issue. A coarse gradient is generated by replacing the a.e. zero derivatives of quantized (i.e., stair-case) ReLU activation composited in the chain rule with some heuristic proxy derivative called straight-through estimator (STE). Although having been widely used in training quantized networks empirically, fundamental questions like when and why the ad-hoc STE trick works, still lacks theoretical understanding. In this paper, we propose a class of STEs with certain monotonicity, and consider their applications to the training of a two-linear-layer network with quantized activation functions for non-linear multi-category classification. We establish performance guarantees for the proposed STEs by showing that the corresponding coarse gradient methods converge to the global minimum, which leads to a perfect classification. Lastly, we present experimental results on synthetic data as well as MNIST dataset to verify our theoretical findings and demonstrate the effectiveness of our proposed STEs.

Global Convergence and Geometric Characterization of Slow to Fast Weight Evolution in Neural Network Training for Classifying Linearly Non-Separable Data

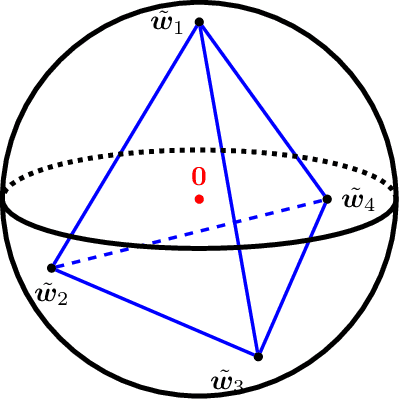
In this paper, we study the dynamics of gradient descent in learning neural networks for classification problems. Unlike in existing works, we consider the linearly non-separable case where the training data of different classes lie in orthogonal subspaces. We show that when the network has sufficient (but not exceedingly large) number of neurons, (1) the corresponding minimization problem has a desirable landscape where all critical points are global minima with perfect classification; (2) gradient descent is guaranteed to converge to the global minima in this case. Moreover, we discovered a geometric condition on the network weights so that when it is satisfied, the weight evolution transitions from a slow phase of weight direction spreading to a fast phase of weight convergence. The geometric condition says that the convex hull of the weights projected on the unit sphere contains the origin.

Understanding Straight-Through Estimator in Training Activation Quantized Neural Nets

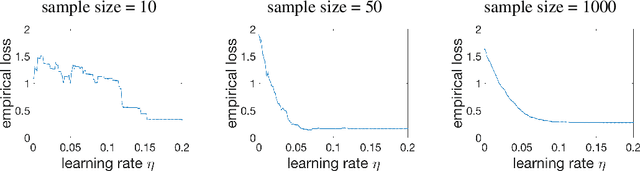
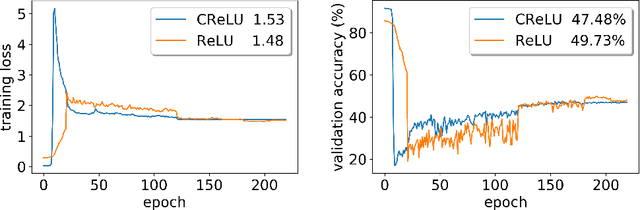
Training activation quantized neural networks involves minimizing a piecewise constant function whose gradient vanishes almost everywhere, which is undesirable for the standard back-propagation or chain rule. An empirical way around this issue is to use a straight-through estimator (STE) (Bengio et al., 2013) in the backward pass, so that the "gradient" through the modified chain rule becomes non-trivial. Since this unusual "gradient" is certainly not the gradient of loss function, the following question arises: why searching in its negative direction minimizes the training loss? In this paper, we provide the theoretical justification of the concept of STE by answering this question. We consider the problem of learning a two-linear-layer network with binarized ReLU activation and Gaussian input data. We shall refer to the unusual "gradient" given by the STE-modifed chain rule as coarse gradient. The choice of STE is not unique. We prove that if the STE is properly chosen, the expected coarse gradient correlates positively with the population gradient (not available for the training), and its negation is a descent direction for minimizing the population loss. We further show the associated coarse gradient descent algorithm converges to a critical point of the population loss minimization problem. Moreover, we show that a poor choice of STE leads to instability of the training algorithm near certain local minima, which is verified with CIFAR-10 experiments.

Non-ergodic Convergence Analysis of Heavy-Ball Algorithms

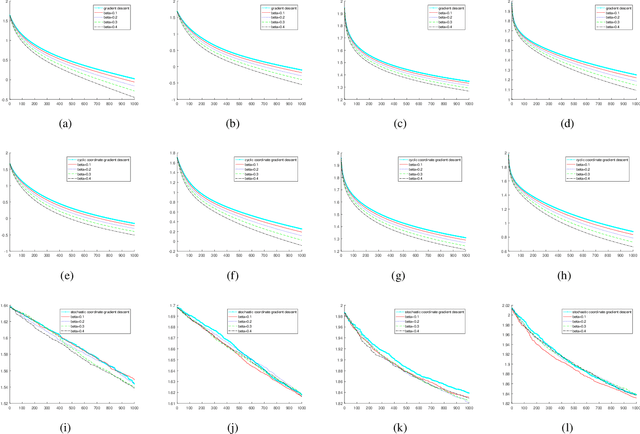
In this paper, we revisit the convergence of the Heavy-ball method, and present improved convergence complexity results in the convex setting. We provide the first non-ergodic O(1/k) rate result of the Heavy-ball algorithm with constant step size for coercive objective functions. For objective functions satisfying a relaxed strongly convex condition, the linear convergence is established under weaker assumptions on the step size and inertial parameter than made in the existing literature. We extend our results to multi-block version of the algorithm with both the cyclic and stochastic update rules. In addition, our results can also be extended to decentralized optimization, where the ergodic analysis is not applicable.

Laplacian Smoothing Gradient Descent

We propose a very simple modification of gradient descent and stochastic gradient descent. We show that when applied to a variety of machine learning models including softmax regression, convolutional neural nets, generative adversarial nets, and deep reinforcement learning, this very simple surrogate can dramatically reduce the variance and improve the accuracy of the generalization. The new algorithm, (which depends on one nonnegative parameter) when applied to non-convex minimization, tends to avoid sharp local minima. Instead it seeks somewhat flatter local (and often global) minima. The method only involves preconditioning the gradient by the inverse of a tri-diagonal matrix that is positive definite. The motivation comes from the theory of Hamilton-Jacobi partial differential equations. This theory demonstrates that the new algorithm is almost the same as doing gradient descent on a new function which (a) has the same global minima as the original function and (b) is "more convex". Again, the programming effort in doing this is minimal, in cost, complexity and effort. We implement our algorithm into both PyTorch and Tensorflow platforms, which will be made publicly available.

Adversarial Defense via Data Dependent Activation Function and Total Variation Minimization

We improve the robustness of deep neural nets to adversarial attacks by using an interpolating function as the output activation. This data-dependent activation function remarkably improves both classification accuracy and stability to adversarial perturbations. Together with the total variation minimization of adversarial images and augmented training, under the strongest attack, we achieve up to 20.6$\%$, 50.7$\%$, and 68.7$\%$ accuracy improvement w.r.t. the fast gradient sign method, iterative fast gradient sign method, and Carlini-Wagner $L_2$ attacks, respectively. Our defense strategy is additive to many of the existing methods. We give an intuitive explanation of our defense strategy via analyzing the geometry of the feature space. For reproducibility, the code is made available at: https://github.com/BaoWangMath/DNN-DataDependentActivation.