Enhancing Zero-Shot Many to Many Voice Conversion with Self-Attention VAE

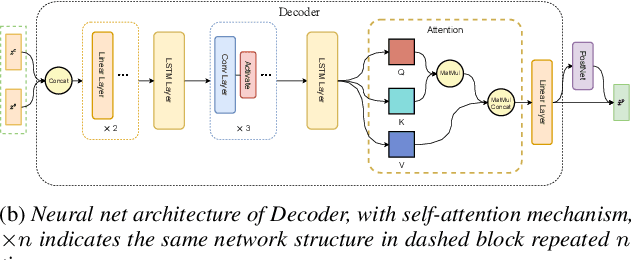
Variational auto-encoder(VAE) is an effective neural network architecture to disentangle a speech utterance into speaker identity and linguistic content latent embeddings, then generate an utterance for a target speaker from that of a source speaker. This is possible by concatenating the identity embedding of the target speaker and the content embedding of the source speaker uttering a desired sentence. In this work, we found a suitable location of VAE's decoder to add a self-attention layer for incorporating non-local information in generating a converted utterance and hiding the source speaker's identity. In experiments of zero-shot many-to-many voice conversion task on VCTK data set, the self-attention layer enhances speaker classification accuracy on unseen speakers by 27\% while increasing the decoder parameter size by 12\%. The voice quality of converted utterance degrades by merely 3\% measured by the MOSNet scores. To reduce over-fitting and generalization error, we further applied a relaxed group-wise splitting method in network training and achieved a gain of speaker classification accuracy on unseen speakers by 46\% while maintaining the conversion voice quality in terms of MOSNet scores. Our encouraging findings point to future research on integrating more variety of attention structures in VAE framework for advancing zero-shot many-to-many voice conversions.

Recurrence of Optimum for Training Weight and Activation Quantized Networks

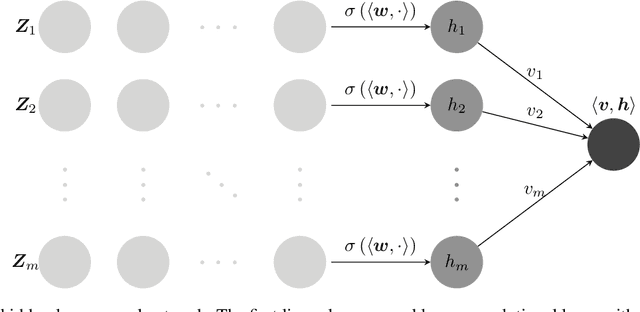
Deep neural networks (DNNs) are quantized for efficient inference on resource-constrained platforms. However, training deep learning models with low-precision weights and activations involves a demanding optimization task, which calls for minimizing a stage-wise loss function subject to a discrete set-constraint. While numerous training methods have been proposed, existing studies for full quantization of DNNs are mostly empirical. From a theoretical point of view, we study practical techniques for overcoming the combinatorial nature of network quantization. Specifically, we investigate a simple yet powerful projected gradient-like algorithm for quantizing two-linear-layer networks, which proceeds by repeatedly moving one step at float weights in the negation of a heuristic \emph{fake} gradient of the loss function (so-called coarse gradient) evaluated at quantized weights. For the first time, we prove that under mild conditions, the sequence of quantized weights recurrently visits the global optimum of the discrete minimization problem for training fully quantized network. We also show numerical evidence of the recurrence phenomenon of weight evolution in training quantized deep networks.

Learning Quantized Neural Nets by Coarse Gradient Method for Non-linear Classification

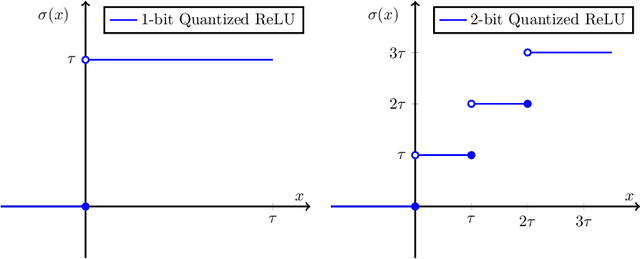
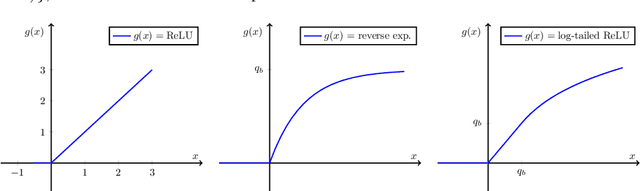
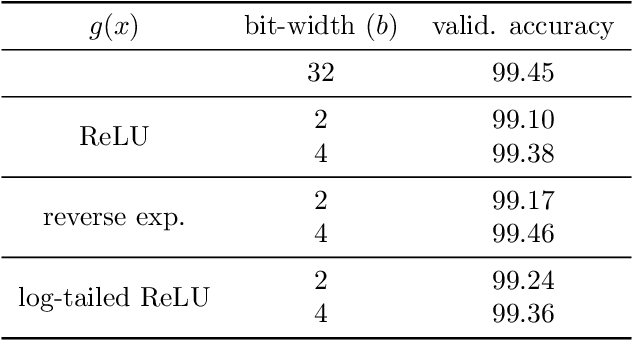
Quantized or low-bit neural networks are attractive due to their inference efficiency. However, training deep neural networks with quantized activations involves minimizing a discontinuous and piecewise constant loss function. Such a loss function has zero gradients almost everywhere (a.e.), which makes the conventional gradient-based algorithms inapplicable. To this end, we study a novel class of \emph{biased} first-order oracle, termed coarse gradient, for overcoming the vanished gradient issue. A coarse gradient is generated by replacing the a.e. zero derivatives of quantized (i.e., stair-case) ReLU activation composited in the chain rule with some heuristic proxy derivative called straight-through estimator (STE). Although having been widely used in training quantized networks empirically, fundamental questions like when and why the ad-hoc STE trick works, still lacks theoretical understanding. In this paper, we propose a class of STEs with certain monotonicity, and consider their applications to the training of a two-linear-layer network with quantized activation functions for non-linear multi-category classification. We establish performance guarantees for the proposed STEs by showing that the corresponding coarse gradient methods converge to the global minimum, which leads to a perfect classification. Lastly, we present experimental results on synthetic data as well as MNIST dataset to verify our theoretical findings and demonstrate the effectiveness of our proposed STEs.

Global Convergence and Geometric Characterization of Slow to Fast Weight Evolution in Neural Network Training for Classifying Linearly Non-Separable Data

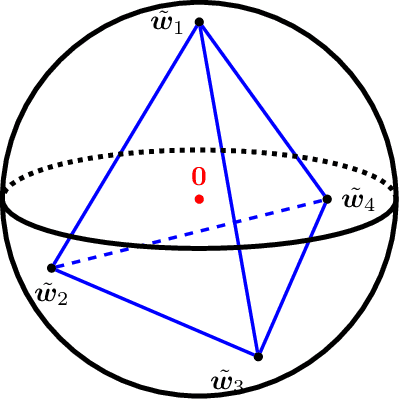
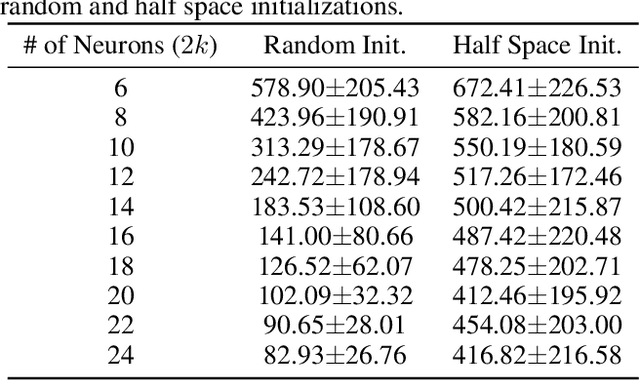
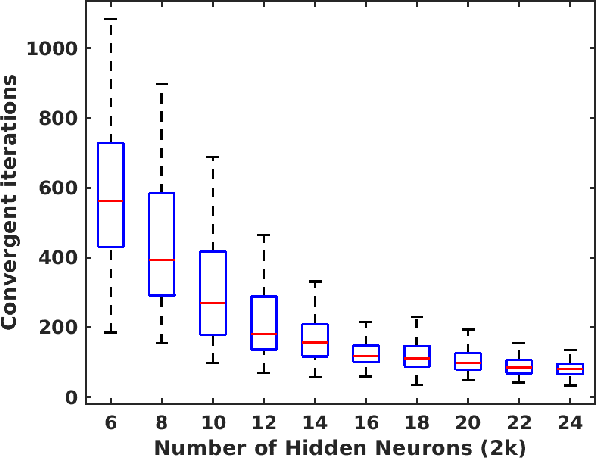
In this paper, we study the dynamics of gradient descent in learning neural networks for classification problems. Unlike in existing works, we consider the linearly non-separable case where the training data of different classes lie in orthogonal subspaces. We show that when the network has sufficient (but not exceedingly large) number of neurons, (1) the corresponding minimization problem has a desirable landscape where all critical points are global minima with perfect classification; (2) gradient descent is guaranteed to converge to the global minima in this case. Moreover, we discovered a geometric condition on the network weights so that when it is satisfied, the weight evolution transitions from a slow phase of weight direction spreading to a fast phase of weight convergence. The geometric condition says that the convex hull of the weights projected on the unit sphere contains the origin.