Learning Quantized Neural Nets by Coarse Gradient Method for Non-linear Classification
Paper and Code
Nov 23, 2020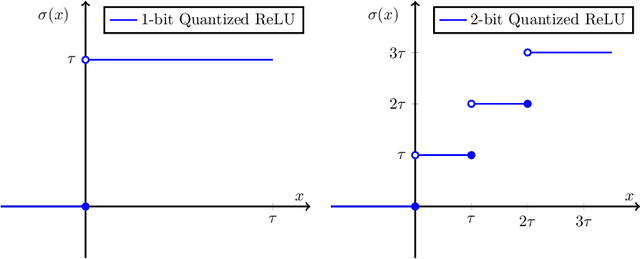

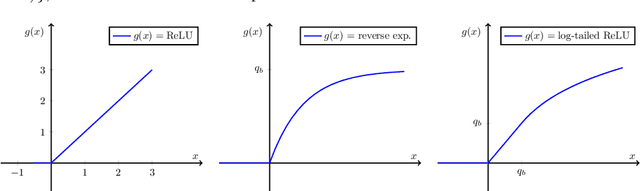
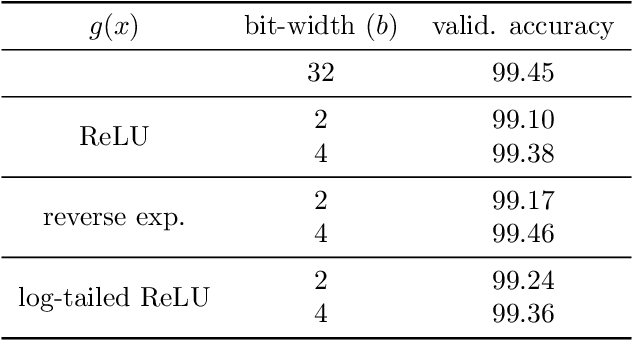
Quantized or low-bit neural networks are attractive due to their inference efficiency. However, training deep neural networks with quantized activations involves minimizing a discontinuous and piecewise constant loss function. Such a loss function has zero gradients almost everywhere (a.e.), which makes the conventional gradient-based algorithms inapplicable. To this end, we study a novel class of \emph{biased} first-order oracle, termed coarse gradient, for overcoming the vanished gradient issue. A coarse gradient is generated by replacing the a.e. zero derivatives of quantized (i.e., stair-case) ReLU activation composited in the chain rule with some heuristic proxy derivative called straight-through estimator (STE). Although having been widely used in training quantized networks empirically, fundamental questions like when and why the ad-hoc STE trick works, still lacks theoretical understanding. In this paper, we propose a class of STEs with certain monotonicity, and consider their applications to the training of a two-linear-layer network with quantized activation functions for non-linear multi-category classification. We establish performance guarantees for the proposed STEs by showing that the corresponding coarse gradient methods converge to the global minimum, which leads to a perfect classification. Lastly, we present experimental results on synthetic data as well as MNIST dataset to verify our theoretical findings and demonstrate the effectiveness of our proposed STEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge