Chun Huang
Low-Complexity Channel Estimation for Extremely Large-Scale MIMO in Near Field
Dec 07, 2023



Abstract:The extremely large-scale massive multiple-input multiple-output (XL-MIMO) has the potential to achieve boosted spectral efficiency and refined spatial resolution for future wireless networks. However, channel estimation for XL-MIMO is challenging since the large number of antennas results in high computational complexity with the near-field effect. In this letter, we propose a low-complexity sequential angle-distance channel estimation (SADCE) method for near-field XL-MIMO systems equipped with uniformly planar arrays (UPA). Specifically, we first successfully decouple the angle and distance parameters, which allows us to devise a two-dimensional discrete Fourier transform (2D-DFT) method for angle parameters estimation. Then, a low-complexity distance estimation method is proposed with a closed-form solution. Compared with existing methods, the proposed method achieves significant performance gain with noticeably reduced computational complexity.Numerical results verify the superiority of the proposed near-field channel estimation algorithm.
Optimizing Streaming Parallelism on Heterogeneous Many-Core Architectures: A Machine Learning Based Approach
Mar 05, 2020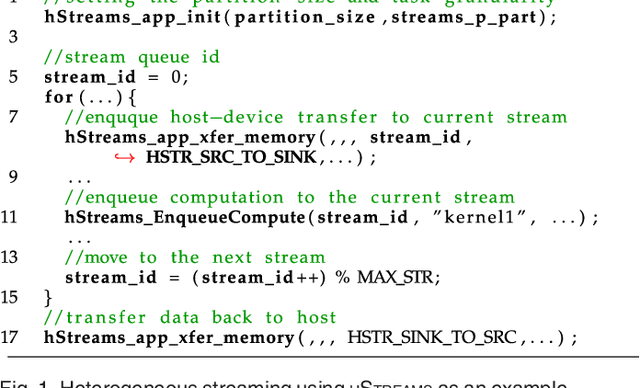

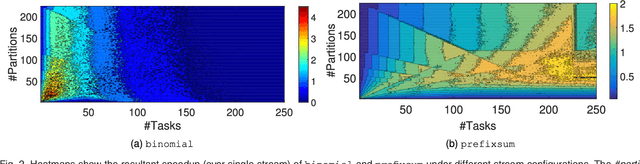
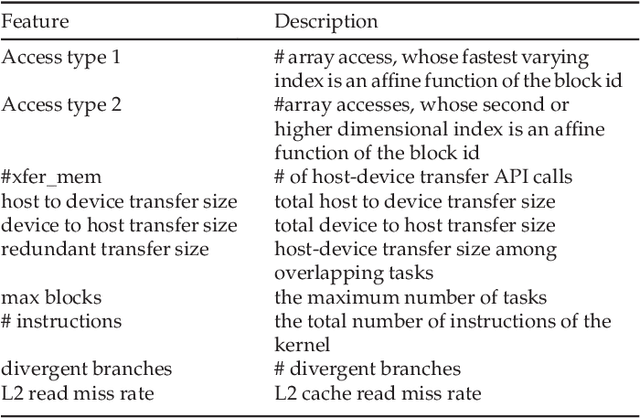
Abstract:This article presents an automatic approach to quickly derive a good solution for hardware resource partition and task granularity for task-based parallel applications on heterogeneous many-core architectures. Our approach employs a performance model to estimate the resulting performance of the target application under a given resource partition and task granularity configuration. The model is used as a utility to quickly search for a good configuration at runtime. Instead of hand-crafting an analytical model that requires expert insights into low-level hardware details, we employ machine learning techniques to automatically learn it. We achieve this by first learning a predictive model offline using training programs. The learnt model can then be used to predict the performance of any unseen program at runtime. We apply our approach to 39 representative parallel applications and evaluate it on two representative heterogeneous many-core platforms: a CPU-XeonPhi platform and a CPU-GPU platform. Compared to the single-stream version, our approach achieves, on average, a 1.6x and 1.1x speedup on the XeonPhi and the GPU platform, respectively. These results translate to over 93% of the performance delivered by a theoretically perfect predictor.
Non-ergodic Convergence Analysis of Heavy-Ball Algorithms
Nov 09, 2018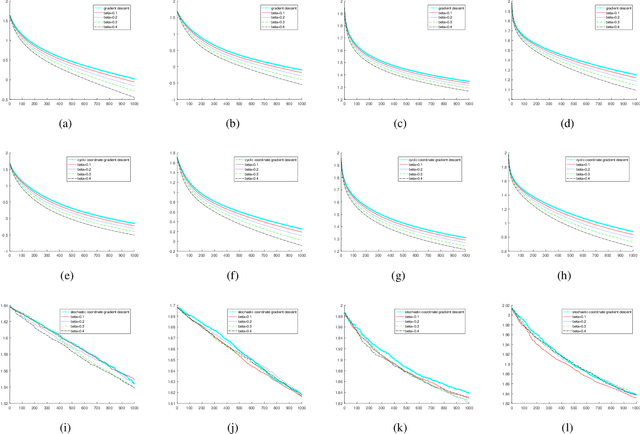
Abstract:In this paper, we revisit the convergence of the Heavy-ball method, and present improved convergence complexity results in the convex setting. We provide the first non-ergodic O(1/k) rate result of the Heavy-ball algorithm with constant step size for coercive objective functions. For objective functions satisfying a relaxed strongly convex condition, the linear convergence is established under weaker assumptions on the step size and inertial parameter than made in the existing literature. We extend our results to multi-block version of the algorithm with both the cyclic and stochastic update rules. In addition, our results can also be extended to decentralized optimization, where the ergodic analysis is not applicable.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge