Crystalformer: Infinitely Connected Attention for Periodic Structure Encoding

Predicting physical properties of materials from their crystal structures is a fundamental problem in materials science. In peripheral areas such as the prediction of molecular properties, fully connected attention networks have been shown to be successful. However, unlike these finite atom arrangements, crystal structures are infinitely repeating, periodic arrangements of atoms, whose fully connected attention results in infinitely connected attention. In this work, we show that this infinitely connected attention can lead to a computationally tractable formulation, interpreted as neural potential summation, that performs infinite interatomic potential summations in a deeply learned feature space. We then propose a simple yet effective Transformer-based encoder architecture for crystal structures called Crystalformer. Compared to an existing Transformer-based model, the proposed model requires only 29.4% of the number of parameters, with minimal modifications to the original Transformer architecture. Despite the architectural simplicity, the proposed method outperforms state-of-the-art methods for various property regression tasks on the Materials Project and JARVIS-DFT datasets.

A Transformer Model for Symbolic Regression towards Scientific Discovery

Symbolic Regression (SR) searches for mathematical expressions which best describe numerical datasets. This allows to circumvent interpretation issues inherent to artificial neural networks, but SR algorithms are often computationally expensive. This work proposes a new Transformer model aiming at Symbolic Regression particularly focused on its application for Scientific Discovery. We propose three encoder architectures with increasing flexibility but at the cost of column-permutation equivariance violation. Training results indicate that the most flexible architecture is required to prevent from overfitting. Once trained, we apply our best model to the SRSD datasets (Symbolic Regression for Scientific Discovery datasets) which yields state-of-the-art results using the normalized tree-based edit distance, at no extra computational cost.

WeaveNet for Approximating Two-sided Matching Problems

Matching, a task to optimally assign limited resources under constraints, is a fundamental technology for society. The task potentially has various objectives, conditions, and constraints; however, the efficient neural network architecture for matching is underexplored. This paper proposes a novel graph neural network (GNN), \textit{WeaveNet}, designed for bipartite graphs. Since a bipartite graph is generally dense, general GNN architectures lose node-wise information by over-smoothing when deeply stacked. Such a phenomenon is undesirable for solving matching problems. WeaveNet avoids it by preserving edge-wise information while passing messages densely to reach a better solution. To evaluate the model, we approximated one of the \textit{strongly NP-hard} problems, \textit{fair stable matching}. Despite its inherent difficulties and the network's general purpose design, our model reached a comparative performance with state-of-the-art algorithms specially designed for stable matching for small numbers of agents.

NeuralLabeling: A versatile toolset for labeling vision datasets using Neural Radiance Fields

We present NeuralLabeling, a labeling approach and toolset for annotating a scene using either bounding boxes or meshes and generating segmentation masks, affordance maps, 2D bounding boxes, 3D bounding boxes, 6DOF object poses, depth maps and object meshes. NeuralLabeling uses Neural Radiance Fields (NeRF) as renderer, allowing labeling to be performed using 3D spatial tools while incorporating geometric clues such as occlusions, relying only on images captured from multiple viewpoints as input. To demonstrate the applicability of NeuralLabeling to a practical problem in robotics, we added ground truth depth maps to 30000 frames of transparent object RGB and noisy depth maps of glasses placed in a dishwasher captured using an RGBD sensor, yielding the Dishwasher30k dataset. We show that training a simple deep neural network with supervision using the annotated depth maps yields a higher reconstruction performance than training with the previously applied weakly supervised approach.

Rethinking Symbolic Regression Datasets and Benchmarks for Scientific Discovery

This paper revisits datasets and evaluation criteria for Symbolic Regression, a task of expressing given data using mathematical equations, specifically focused on its potential for scientific discovery. Focused on a set of formulas used in the existing datasets based on Feynman Lectures on Physics, we recreate 120 datasets to discuss the performance of symbolic regression for scientific discovery (SRSD). For each of the 120 SRSD datasets, we carefully review the properties of the formula and its variables to design reasonably realistic sampling range of values so that our new SRSD datasets can be used for evaluating the potential of SRSD such as whether or not an SR method con (re)discover physical laws from such datasets. As an evaluation metric, we also propose to use normalized edit distances between a predicted equation and the ground-truth equation trees. While existing metrics are either binary or errors between the target values and an SR model's predicted values for a given input, normalized edit distances evaluate a sort of similarity between the ground-truth and predicted equation trees. We have conducted experiments on our new SRSD datasets using five state-of-the-art SR methods in SRBench and a simple baseline based on a recent Transformer architecture. The results show that we provide a more realistic performance evaluation and open up a new machine learning-based approach for scientific discovery. Our datasets and code repository are publicly available.

Edge-Selective Feature Weaving for Point Cloud Matching

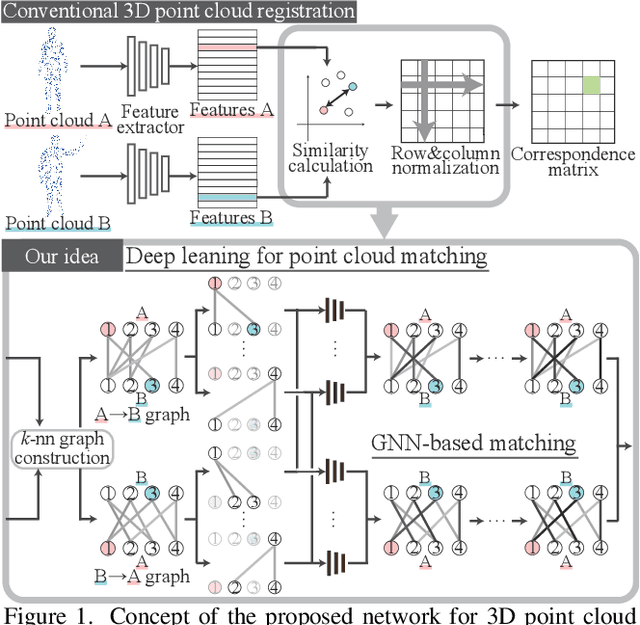
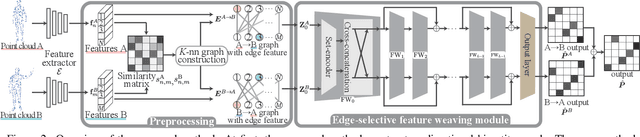
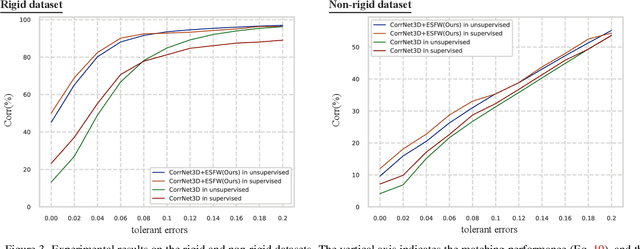
This paper tackles the problem of accurately matching the points of two 3D point clouds. Most conventional methods improve their performance by extracting representative features from each point via deep-learning-based algorithms. On the other hand, the correspondence calculation between the extracted features has not been examined in depth, and non-trainable algorithms (e.g. the Sinkhorn algorithm) are frequently applied. As a result, the extracted features may be forcibly fitted to a non-trainable algorithm. Furthermore, the extracted features frequently contain stochastically unavoidable errors, which degrades the matching accuracy. In this paper, instead of using a non-trainable algorithm, we propose a differentiable matching network that can be jointly optimized with the feature extraction procedure. Our network first constructs graphs with edges connecting the points of each point cloud and then extracts discriminative edge features by using two main components: a shared set-encoder and an edge-selective cross-concatenation. These components enable us to symmetrically consider two point clouds and to extract discriminative edge features, respectively. By using the extracted discriminative edge features, our network can accurately calculate the correspondence between points. Our experimental results show that the proposed network can significantly improve the performance of point cloud matching. Our code is available at https://github.com/yanarin/ESFW